Chapter 2: Measurement uncertainty and significant figures

Imagine that you make a series of simple measurements on a group of people (e.g., patients in your care or subjects in your study). One of the measurements is height, which you record using a stadiometer (an instrument for measuring people’s height) with 1 mm graduations. For a group of 3 people you measure their heights to be 167.8 cm, 178.2 cm and 175.8 cm and determine the mean. Your calculator will give you a result like this:

It is tempting to trust the number on the calculator, but is it right? How would you report this number?

Any measurement has a degree of uncertainty. This is because any tool or instrument we use for measuring has a limited capacity for precision; even our senses themselves have limitations. One way to describe the certainty we have about a measurement is by the number of digits we use when reporting the measurement. We call this the number of significant figures.

In the above example, the mean height should be reported as 173.9 cm. It would be misleading to use more decimal places because the stadiometer is only precise for 1 mm increments.

Determining the number of significant figures to use to express a final answer in a calculation can become complicated when you need to incorporate different measurements with different degrees of precision. Often you need to think about where the data comes from or how the measurement was made. The key rule to remember when reporting a final number, which was dependent on several measurements, is this:

Your answer should be reported in such a way that it reflects the reliability of the least precise measurement. That is, the number of significant figures in your answer will be limited to the measurement with the lowest number of significant figures.

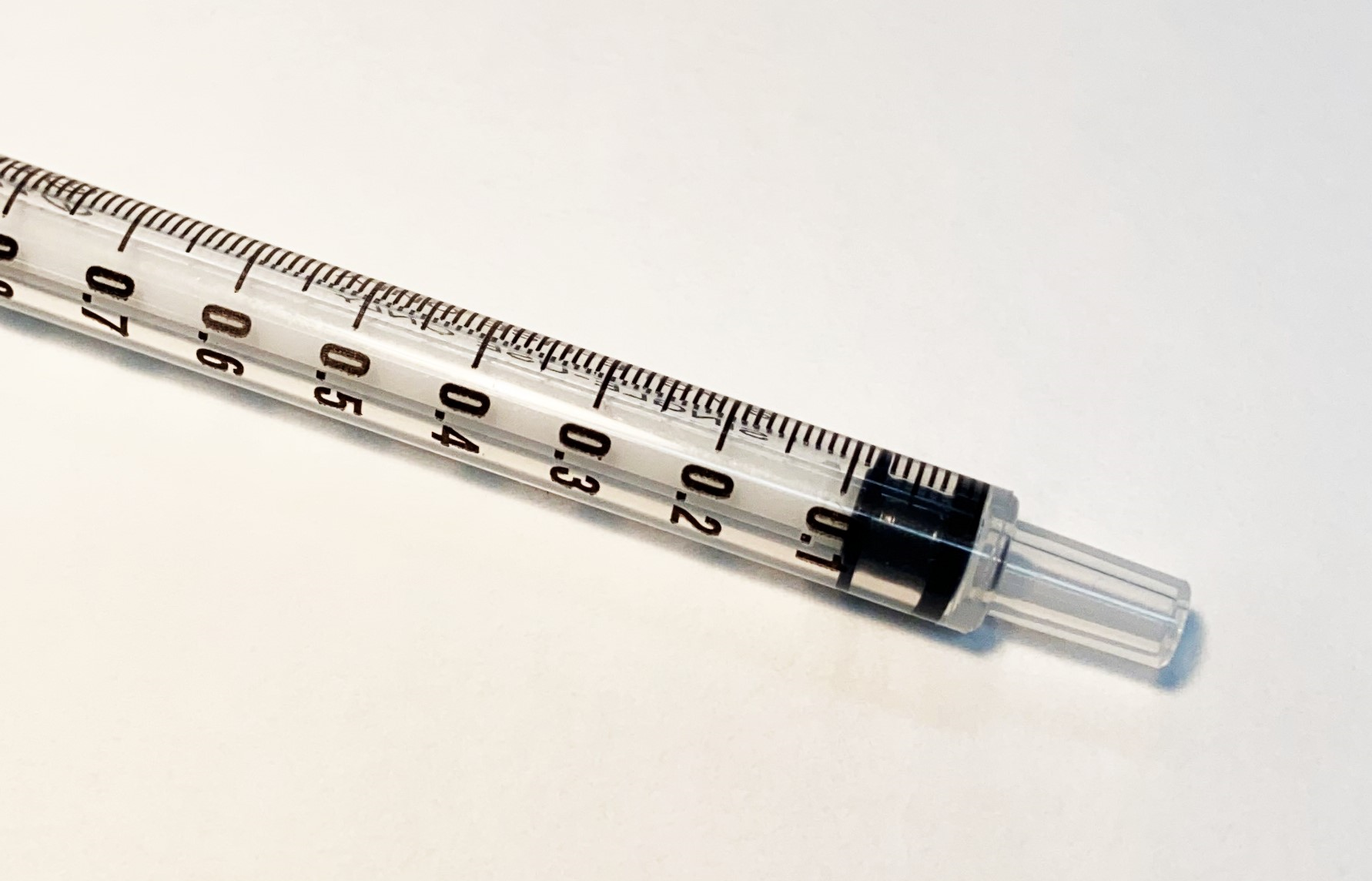
Measurement precision

How precise is this 1 ml syringe?

The major markings are at 0.1 ml increments and there are 9 markings between these creating 10 divisions. This means that, since 0.1 divided by 10 is 0.01, this syringe is accurate to measurements as small as 0.01 ml (1/100th of a ml)*.

Using this syringe, you could report that 0.45 ml was injected. However, it would be incorrect to report that 0.452 ml was injected as the syringe is not precise to 1/1,000th of a ml.

*In actual practice, for this syringe even an accuracy of 0.01 ml may be an overestimation. Most 1 ml syringes are rated at about 5% accuracy.  Accuracy is often indicated on apparatus as /- followed by the percentage value of accuracy. For a 1 ml syringe rated with /- 5% accuracy, this means that we know, at best that measuring a 1 ml volume in that syringe will deliver somewhere between 0.95 and 1.05 ml.