1.4 Diagnostic test answers

1. 40 / (120 + 40) =

Complete the bracketed component first:

40/160 × 6 =

Simplify by dividing the fraction by 10:

4/16 × 6 =

1/4 × 6 = 1.5

Being able to do simple arithmetic is important for all calculations. A key skill is being able to quickly estimate the magnitude of an answer to avoid mistakes – see Chapter 3: Estimation (sanity checking). Being able to understand the order of operations is crucial for being able to solve for unknowns – see Chapter 10: Correlation, causation and confounding variables and Chapter 12: Growth and decay – Exponents and logarithms.

2. (0.2/2) × 500 =

Again, it helps to simplify, and recognising that 0.2 is 1/10th of 2 helps here:

(1/10) × 500 = 50

Again, the key skill being taught here is to quickly estimate the magnitude of an answer – see Chapter 3: Estimation (sanity checking).

3. How many milligrams are in 1.25 g?

The prefix milli denoted by ‘m’, in front of the base unit grams denoted by ‘g’, means one thousandth (1/1,000). That is, there are 1,000 mg in 1 g.

Therefore, the answer is 1,000 mg × 1.25 = 1,250 mg

If you are unfamiliar with the SI units and their prefixes, this is covered in Chapter 5: Scientific notation and SI units and Chapter 4: Biological scale. Being able to quickly interconvert between units is essential to be able to work with concentrations and volumes of solutions – see Chapter 7: Solutions and concentrations and Chapter 8: Dilutions.

4. How many µl are in 0.68 ml?

The prefix micro denoted by ‘µ’, in front of the base unit litres denoted by ‘l’, means one millionth (10^–6). That is, there is 10⁶ (1 million) µL in 1 L and 10³ (1 thousand) µl in 1 ml.

Therefore, the answer is 1,000 µl × 0.68 = 680 µl

As in question 3 above, if you are unfamiliar with the SI units and their prefixes, this is covered in Chapter 5: Scientific notation and SI units. Being able to quick interconvert between units is essential to be able to work with concentrations and volumes of solutions – see Chapter 7: Solutions and concentrations and Chapter 8: Dilutions.

5. How many significant figures are in each of the following measured values?
   1. 50,000

There is 1 significant figure as trailing zeros following a whole number are not considered significant unless the decimal is shown (e.g., 50,000.0) or it is referring to an exact number in which case there are infinite significant figures (e.g., 50,000 people) or the significant figure is denoted by an overbar (e.g., 50,00).

1. 1. 100.3

There are 4 significant figures as all non-zero numbers are significant and any zeros between significant numbers are significant.

Significant figures are important when thinking about measurements and how precise they are – see Chapter 2: Measurement uncertainty and significant figures.

6. Write 0.00361 in scientific notation.

3.61 × 10^–3

Quite often, numbers are too big or small to use conveniently. It is common practice to write these numbers as two numbers multiplied, almost always using exponents of base 10 – see Chapter 5: Scientific notation and SI units.

7. Write 1.35 × 10^–2 in decimal notation.

0.0135

Being able to interconvert scientific notation and decimal notation is important, particularly when working with SI units and prefixes – see Chapter 5: Scientific notation and SI units.

8. How many moles are in 60 g of NaOH? (The molar mass of Na is 23 g/mol, of O is 16 g/mol and of H is 1 g/mol.)

First you need to calculate the molecular mass of 1 mole of NaOH:

23 + 16 + 1 = 40

Then determine the number of moles in 60 g:

60/40 = 1.5 moles

Understanding the concept of molecular weight (molecular mass) and the mole is essential to be able to understand and work with concentrations, which are often expressed as moles per litre – see Chapter 7: Solutions and concentrations.

9. Sunwise Lime Cordial is sold as a 10x concentrate. How much concentrate would you need to make 500 ml of 1x cordial?

We are diluting the cordial by a factor of 10 – that is, going from 10x to 1x – therefore we only need a 1/10th of the final volume of the undiluted (10x) cordial.

(1x/10x) × 500 ml =

(1/10) × 500 ml = 50 ml

This is essentially the same problem as in question 2 but this time just put into words. Being able to work with ratios and perform dilutions is covered in Chapter 8: Dilutions.

10. What is the final concentration of a solution where 40 ml of a 6 M solution is added to 120 ml of water?

This is the same problem as question 1 but this time put into words to make it more confusing!

We are adding 40 ml of a 6 M solution into a total volume of 40 ml + 120 ml, so the concentration should decrease by the amount of dilution.

= (40 ml / (120 ml + 40 ml)) × 6 M

= (40/160) × 6 M

= 4/16 × 6 M

= 1/4 × 6 M = 1.5 M

For help with problems similar to this, see Chapter 8: Dilutions.

11. If you had 1 l of a 2 M stock solution of NaCl but need 500 ml of a 0.2 M solution of NaCl, how much of your stock solution would you need to use to prepare your final solution?

You might recognise this problem as being similar to questions 2 and 9 but this time it has been made more difficult by including ‘scientific’ terms and by including some irrelevant information.

A good way to solve this is by using the formula C₁V₁ = C₂V₂ where C₁ refers to the initial concentration and C₂ the final concentration while V₁ refers to the initial volume and V₂ to the final volume. The initial volume V₁ is what we need to determine.

V₁ = ? ml

C₁ = 2 M

V₂ = 500 ml

C₂ = 0.2 M

So, you can now see that volume of the stock solution is not relevant to the question. (Unless there was not enough of it!)

C₁V₁ = C₂V₂

So, 2 M × V₁ = 500 ml × 0.2 M

It is important to have the same units for volume and concentration on each side of the equation here.

V₁ = (0.2 M / 2 M) × 500 ml = 50 ml

For help with problems like this, see Chapter 8: Dilutions.

12. Which of these is equivalent to ?

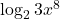b. as per the general rule

This rearrangement is important for being able to solve for unknown exponents in growth and decay formulas – see Chapter 12: Growth and decay – Exponents and logarithms.

13. A DNA stock solution with a concentration of 100 µg/ml was diluted to make 3 other sequential solutions. That is, for each dilution, 1 ml of the previous solution was added to 4 ml of water for a final volume of 5 ml. What is the concentration of the final solution?

Each of these dilutions is a 1 in 5 dilution; that is, 1 ml is added into a total volume of (1 ml + 4 ml) 5 ml.

When the dilutions are carried out in series like this the dilution factors are multiplied:

1/5 × 1/5 × 1/5 × 100 µg/ml = 0.8 µg/ml

In this way, using serial dilutions, a large but accurate dilution can be made that does not require a massive volume of solvent – see Chapter 8: Dilutions.

14. For the dataset 10, 20, 25, 20, 20, 10, 25, 30, 20, calculate the:
    1. Mean: The mean is equal to the sum of the data divided by the number of data entries.Mean = sum of data/n = 180/9 = 20
    2. Mode: Mode is the most common value in data set = 20
    3. Range: Range is the absolute spread the data can be expressed as: 10–30 (or 20)

For working with descriptive statistics see Chapter 9: Medical diagnostics – Measurement, uncertainty and distributions.

15. There are 5 mice in a cage; 2 of them are known to have the QLIT mutation. What is the percentage chance that a researcher who picks 2 mice at random will choose both mice with the QLIT mutation?

There is a 2/5 chance of initially picking a QLIT mouse and then because of non-replacing selection there is a 1/4 chance of the second mouse being QLIT.

Therefore, chance = 1/5 × 1/4 = 2/20 = 1/10

Understanding probability is a vital skill and is especially important in being able to understand the sensitivity and specificity of medical diagnostic tests – see Chapter 10: Medical diagnostics – Sensitivity and specificity.

16. Which of the following correlation coefficients (r) represent the strongest relationship between two variables?

c. r = –0.6

The strength of the correlation between two variables can be estimated by the correlation coefficient, r. The closer r is to either –1 or 1 the stronger the correlation. That is, the absolute value of the correlation coefficient gives us the strength of the relationship.

For more information about bivariate analysis (the relationship between two variables) and correlation, see Chapter 11: Correlation, causation and confounding variables.

17. The rate of growth for a species of mesophilic bacteria was determined across a range of temperatures. The resulting graph is shown below.

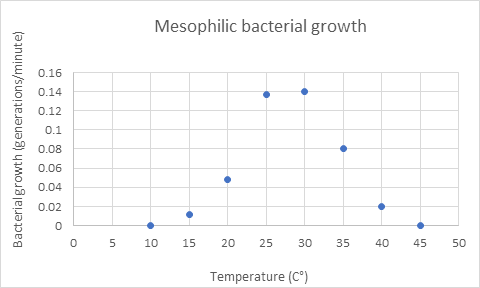
1. 1. From the graph, what is the temperature range where bacterial growth is possible? 15 to 40°C
      Bacterial growth does not occur at 10°C or 45°C and you cannot extrapolate from 10–15°C and 40–45°C.
   2. From the graph, what is the temperature range where would you expect maximal bacterial growth?
      Between 25 and 30°C.

18. A range of BSA concentrations were analysed using a colorimetric assay. The absorbance values at 750 nm were plotted against BSA concentrations, as shown in the graph below.

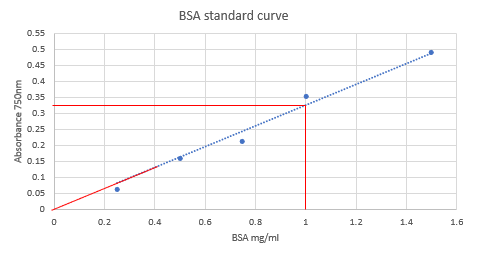
1. 1. What would be the likely concentration for an unknown BSA solution which had an absorbance of 0.325 using the assay above?

The concentration corresponding to the absorbance value can be determined from the line of best fit. Draw a horizontal line from the absorbance value of 0.325 to the line of best fit. Where it intercepts, draw a vertical line down to the x-axis and read the concentration. In this case the concentration is 1 mg/ml.

1. 1. What absorbance would you expect for a solution containing 0.1 mg/ml BSA using the assay above?

Extrapolate the line of best fit down, to the point 0,0. You can see that the answer should be approximately 0.025 (note that absorbance does not have units).Just as a note, 0,0 is a valid point and can be included to calculate the line of best fit, but it is not strictly valid to force the line through 0,0. Occasionally you will see this and in general it is done in error or to ensure that nonsensical negative values are avoided.

Absorbance and spectrophotometry are covered in Chapter 7: Solutions and concentrations. More detail on linear regression is provided in Chapter 11: Correlation, causation and confounding variables.

19. Human blood plasma normally has an H⁺ concentration of 10^–7.4 M. What is the pH of human blood plasma? (Note that pH = –log₁₀[H⁺] where [H⁺] is the H⁺ concentration in M.)

This is solved by substituting the H⁺ concentration into the equation:

The exponent can be brought to the front of the equation, changing the sign in the process:

Since log₁₀ of 10 = 1

Further information about working with logarithms and exponents is provided in Chapter 13: Growth and decay – Exponents and logarithms.

20. What is in the equation below?

This is solved using the general rule

Therefore,

Again, further information on the fundamental rules for working with logarithms and exponents is found in Chapter 13: Growth and decay – Exponents and logarithms.