2.1 Rules for significant figures
There are three rules for deciding how many significant figures there are in a number.
1. Non-zero digits are always significant
This rule should be self-explanatory. If you weigh out a chemical on an analytical balance and the mass is 1.38 g, then all these numbers are significant as a measurement has been made to their precise value.
2. Any zeros between two significant digits are significant
This time you weigh out a chemical on a balance and the mass is 203 mg. From rule 1, the numbers 2 (hundreds) and 3 (ones) are significant. However, the measurement also applies to the 0 (tens) as the value of the tens has been used to determine the value of the ones. Thus, the mass, 203 mg has 3 significant figures.
3. A final zero or trailing zeros in the decimal portion ONLY are significant
This is the more difficult rule. Imagine that you express the mass of the chemical from rule 1 in kg. The value would be 0.00138 kg.
The first zero (0.) is there to indicate the position of the decimal point – it could be left off if you chose to do so.
The next two zeros (.00) are only placeholders to put the decimal point in the correct position. If the number is written in scientific notation (1.38 × 10–3) they disappear.
If the mass was measured at 1.00 g, then both these zeros are significant as a decision has been made on their value (i.e. that was the precise reading on the balance).
If there are trailing zeros in a whole number (e.g. 500) these zeros are NOT significant.
For example, 55,000 has only 2 significant figures.
But it is possible that 55,000 can be expressed as having more than 2 significant figures. If this is the case, you will be told (hopefully). There are a few ways to indicate if a trailing zero is significant:
- 55,0
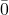0 – an overbar (rare). This number has 4 significant figures. - 55,000. – a decimal point (rare). This number has 5 significant figures.
- 5.5000 × 104 – scientific notation. This number has 5 significant figures.
Important
Exact numbers are numbers that we use for counting (e.g. 4 people, 6 pencils) and are considered to have an infinite number of significant figures, so you do not need to worry about these in your calculations (see the next section). For example, if you count the number of people in a room then the number has an infinite number of significant figures. If there are precisely 4 people, then there are 4.00000000 (etc.) people.
Defined numbers are also exact numbers. For example, there are 1,000 g in a kg. Or there are 1 carbon and 2 oxygen atoms in a molecule of carbon dioxide.
