12.5 Boffin questions
Exponential bias
In the famous fable known as the Wheat and Chessboard problem, the ancient Indian mathematician Sessa (alternatively known as Sissa) invented the game of chess. His king upon seeing the game was so impressed he asked Sessa to name his reward. Sessa asked for a single grain of wheat (in some versions of the story it is a grain of rice) to be placed in the first square of the chessboard, two in the second, four in the third and so on – doubling each time. The king agrees, thinking it a very small reward. The king’s treasurer, who was much less arithmetically challenged, was incredibly dismayed with this agreement!
- Can you work out the amount of wheat Sessa would be owed?
The king in the fable exhibits what is known as exponential bias. Many people underestimate how fast an exponential function can increase in value. Epidemiologists are often frustrated by this when trying to introduce control measures to limit the spread of contagions. The most effective way to stem the spread of a pandemic such as COVID-19 is social distancing, but the introduction of such measures is hampered if a sizeable part of the population fails to see the need as they focus on the initial low numbers of infections.
- The following data on the number of COVID-19 cases in Canada during the early stages of the pandemic in 2020 are presented in the next figure in two different ways.
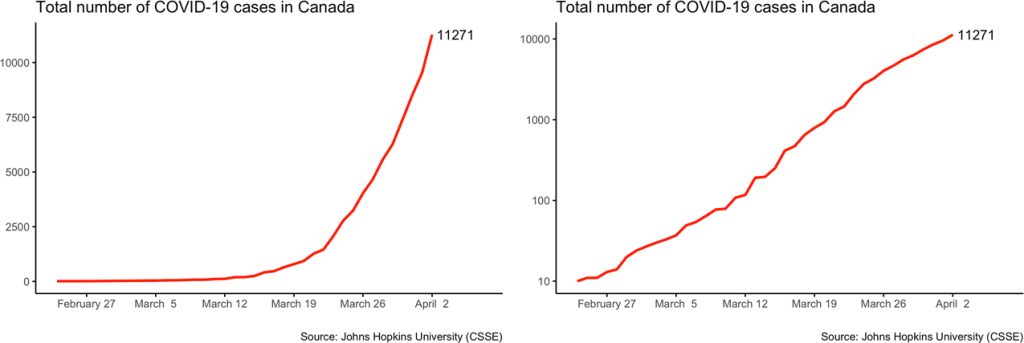
Which presentation do you think would be more effective at convincing the Canadian public that social distancing measures were required?
- Imagine that in a particular country a COVID-10 outbreak occurs. Initial testing shows that 23 people have been infected so far. Modelling predicts that the number of infected people will grow by 28% per day. The country’s government wants to push back the moment when 1,000,000 people are infected as much as possible so as to not overwhelm the healthcare sector. Therefore, they wish to adopt increased handwashing to reduce infection rates. Modelling suggests that with these measures the number of infected people would grow at 21% per day.
- How much time would the country gain with these measures until 1,000,000 people are infected?
- How many infections could be avoided in the following 30 days with these measures?
What is the unit for pH?
The short answer to this is that pH is dimensionless; that is, it has no units. You may recall that pH is defined as the negative log10 of the hydrogen ion concentration expressed in mol L–1.
![\displaystyle \text{pH} = -\log_{10}[\text{H}^{+}]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-729446c5eda2639f68bad8ba91d622fa_l3.png "Rendered by QuickLaTeX.com")
So, why does pH have no units? You can also think of the equation as:
This could be expanded as the sum of the logs of the different units (see the section above on working with logs), which does not make sense.Instead, before taking the logarithm, we have to divide the hydrogen ion concentration by the unit of concentration (M or mol L–1) in order to obtain a dimensionless or unitless number. What we are really doing is this:
But you will almost never see the equation for determining pH written like this in a textbook!
Logarithms are what is known in mathematics as a transcendental function. A transcendental function is one which cannot be expressed as an algebraic function. Examples of transcendental functions include the exponential function and its logarithmic inverse as well as trigonometric functions such as sin.
