12.4 Practice problems

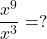
- Rewrite in logarithmic form.
- Rewrite 103 = 1,000 in logarithmic form.
- Rewrite logx y = z in exponential form.
- Rewrite log3 1 = 0 in exponential form.
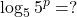
- True or false:
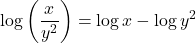
- True or false:
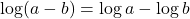
- True or false:
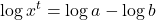
- True or false:
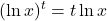
- Solve for x:
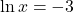
- What is x, when
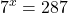
- Calculate
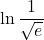
- What is the approximate hydrogen ion concentration [H+] of blood with pH 7.4?
- A bacterial population with a starting population of 50 doubles every 20 minutes under ideal conditions. Which equation best describes the growth of the bacterial population?
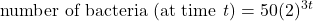 , where t = hours
, where t = hours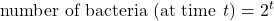 , where t = hours
, where t = hours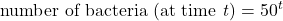 , where t = hours
, where t = hours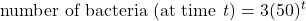 , where t = hours
, where t = hours
- A certain type of bacteria, given a favourable growth medium, doubles in population every 8 hours. Given there were approximately 1,000 bacteria to start with, how many bacteria will there be in 2.5 days?
- The mad scientist Dr Herbert West accidently causes a zombie outbreak on a small Pacific island. The zombie outbreak can be modelled by the following exponential equation:
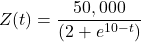
where Z is the number of zombies after t days.- After 5 days, approximately how many zombies are there?
- What is the maximum number of people that can turn into zombies?
- Electrocardiograms (ECGs) are most often used by clinicians to identify potential arrhythmias. The QT interval on an ECG is the time interval representing ventricular depolarisation and subsequent repolarisation (i.e. the duration of activation and recovery of the heart). The RR interval on an ECG is the interval used to calculate the heart rate. The QT interval varies with heart rate (i.e. RR interval) and can be modelled using the following function:
QT= 425 – 676 · e–0.0037·RR
where RR is the RR interval from an ECG (all units are in milliseconds).
What is the QT interval for an individual with an RR interval of 850 ms? Answer to the nearest whole millisecond. - Using the ECG formula for the QT interval
QT= 425 – 676 · e–0.0037·RR
determine the RR interval for a patient with a QT interval of 330 ms. Answer to the nearest whole millisecond. - The area of a wound decreases exponentially with time. The area A of a wound after t days can be modelled by
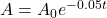 where latex] A_{0}[/latex] is the initial wound area. If the initial wound area is 4 cm2, how many days until the wound is 50% of its initial size?
where latex] A_{0}[/latex] is the initial wound area. If the initial wound area is 4 cm2, how many days until the wound is 50% of its initial size?
![]()
Solution to Practice Problem 12.14.
Solution to Practice Problem 12.16.

