6.1 Counting cells

The device shown in the next figure is used for accurately determining cell concentrations. It is known as a haemocytometer, since it was originally designed for performing blood cell counts. However, it is also used for cell culture, microbiology or any application where it is necessary to determine the number of cells per unit volume of a suspension.

 

A photograph of a haemocytometer slide with a coverslip.
Figure 6.4: Haemocytomer used for counting cells. Photo by Julian Pakay.

 

A haemocytometer is a modified and calibrated microscope slide which has two coverslip supports precisely raised above a cell counting surface inscribed with a precise grid, as shown in the next figure. This creates a defined volume for counting cells in suspension, which are pipetted into the counting chamber.

 

A diagram of the counting chamber of a haemocytometer demonstrating the 0.1 nm depth of the chamber with an expanded view of the surface of the counting chamber showing its dimensions.
Figure 6.5: A haemocytometer counting chamber (Adapted from ‘Using a Counting Chamber’ created by David R. Caprette from Rice University.)

 

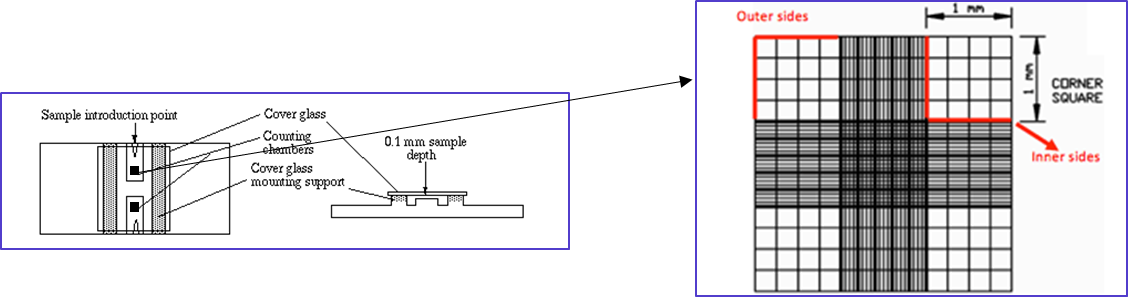
Care is taken to dilute the cell suspension, so it is not so crowded it is impossible to count and also so that the cells are uniformly distributed. Often a dye is added to the cells which distinguishes dead cells from viable cells. The cell suspension is pipetted slowly into the counting chamber, which fills by capillary action. For most mammalian cell suspensions, the large corner squares (1 mm × 1 mm) are used for counting but smaller squares may be used for smaller cells such as erythrocytes or yeast. The cells are counted while viewing the haemocytometer under a microscope. Counting is done systematically to avoid bias. For instance, cells that overlap a line count as ‘in’ if they overlap the top or right outer line, and ‘out’ if they overlap the bottom or left outer line.

 

Calculating cell concentrations from a haemocytometer

A typical depth for a haemocytometer counting chamber is 0.1 mm. Therefore, the volume defined by one of the 1 mm outer squares is:

height x width x depth = volume

1 mm × 1 mm × 0.1 mm = 0.1 mm3

(there are 1,000 mm3 in 1 cm3 and 1 cm3 = 1 ml)

Therefore, 0.1 mm3 = 1 ml/1,000 mm3 x 0.1 mm3 = 0.0001 ml = 0.1 µl

 

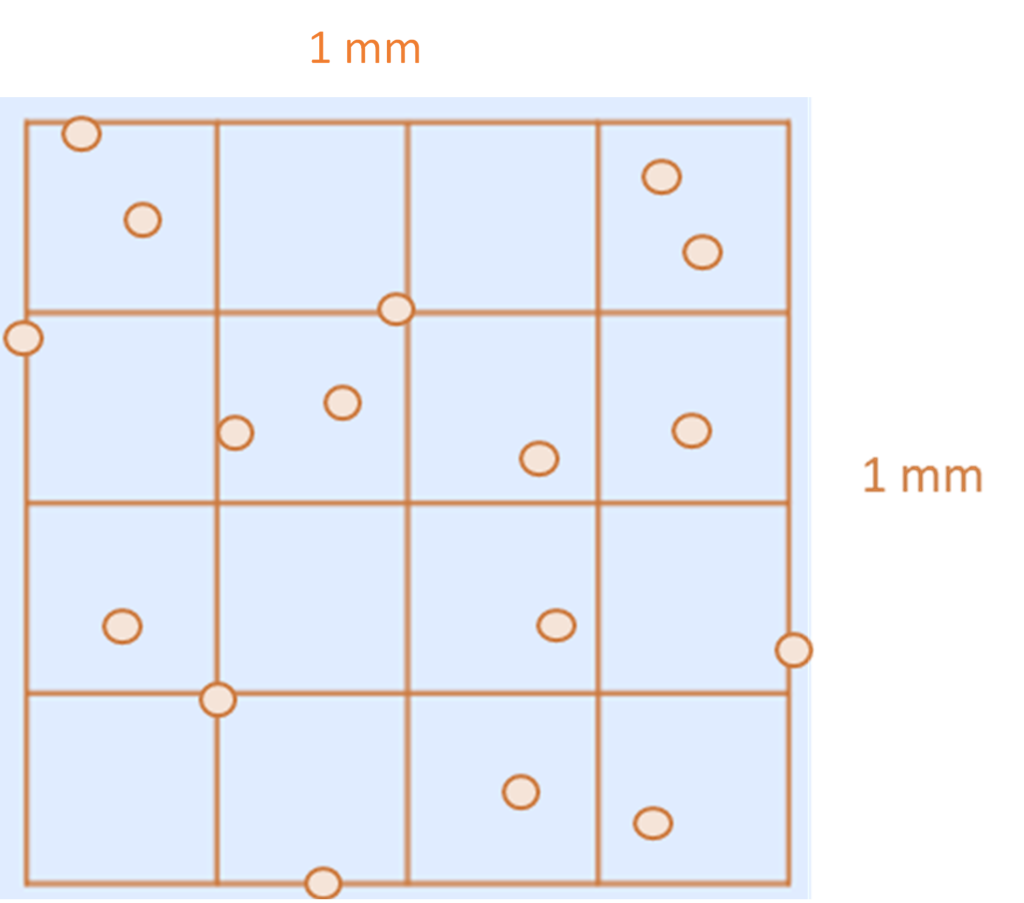
A diagram of one of the corner squares from the counting chamber with circles representing cells. Some of the cells straddle the outer perimeter of the chamber showing the need to have a systematic approach to counting the cells to ensure consistent inclusion and exclusion of cells.
Figure 6.6: A diagram showing one of the outer corner squares from. The circles represent cells. Since some cells straddle the outside border, a methodical approach is required to ensure consistent counting.

 

In the 1 mm × 1 mm square above, there are 15 cells (counting to avoid bias). Assuming this is representative of the cell suspension they were aliquoted from; this means that cell suspension contains:

15 cells per 0.1 µl

which is 150 cells per µl

which is 150,000 cells per ml.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Foundations of Biomedical Science: Quantitative Literacy: Theory and Problems Copyright © 2023 by La Trobe University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book