28 Triangles

We now turn from the proofs we obtain in geometric constructions to the geometry of length, area and volume.

Some key measurable properties of shapes we are often interested in are:

For 2-dimensional shapes

• Perimeter – the length around the outside of a shape
• Area – how many square units fit inside a shape

For 3-dimensional shapes

• Surface Area – how many square units could be used to wrap or cover the shape
• Volume – how many cubic units fit inside a shape

Triangles

Triangles will be our starting point for determining the some general rules for area and volume, as well as the properties of angles in other shapes.

You probably already know that triangles can be classified in three ways:

• Equilateral, with sides of equal length, and equal angles
• Isosceles, two sides are the same, two angles are the same
• Scalene, different length sides and angles.

This kind of equivalency between angle property descriptions and side property descriptions does not happen with other shapes, e.g. with quadrilaterals, equal angles (squares, rectangles) does not imply equal side lengths (squares, rhombuses). If you spent a while playing Euclidea, you will have probably figured out that triangle play a key role in helping to establish the angle properties of other shapes.

Many of the properties of triangles can be worked out from the way angles preserve ratio, or the concept of ‘similar triangles’.

This is useful because it means a lot of what we can deduce about unknown lengths and, subsequently, areas will just amount to ratio problems.

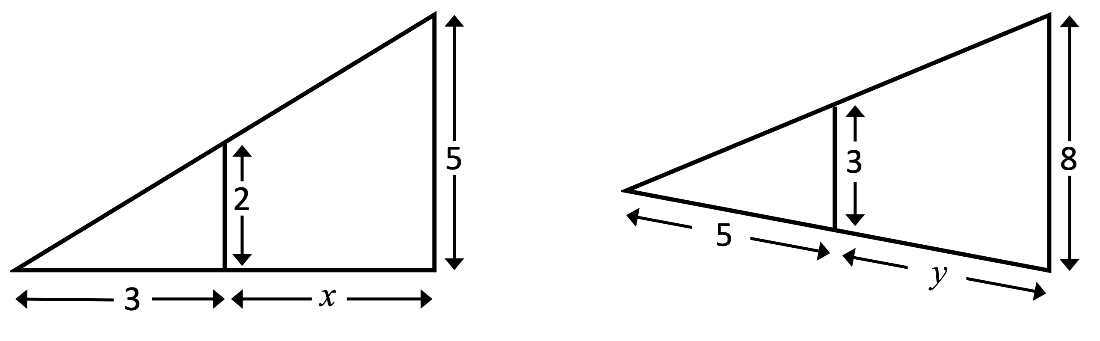
In fact, for right-angled triangles, some of the ratios between sides and how they relate to particular angles have special names and rules.  These are the (fairly well known for at least 2,000 years) sine, cosine and tangent rules.

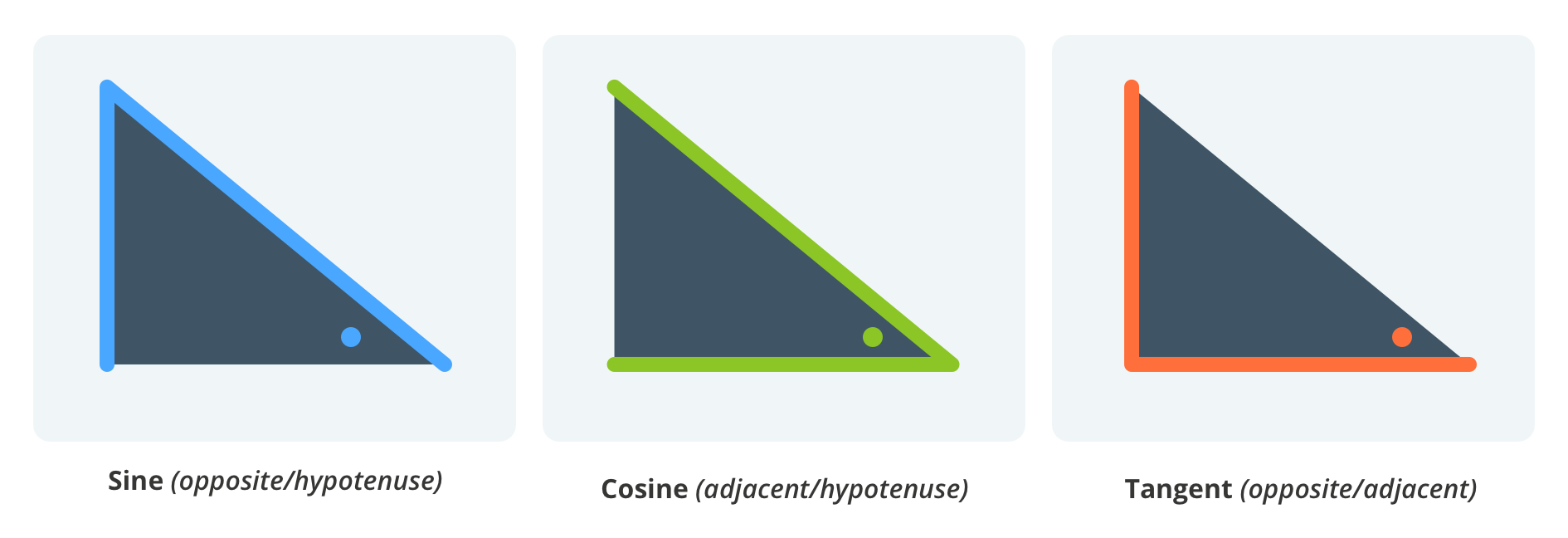
These rules work because if we consider triangles with a right angle, the angle will automatically determine each of these ratios.  In fact, sometimes the steepness of angles are described in terms of ratios, e.g. on the road when you see a sign that says 15% decline – it means that the road goes downwards 15cm for every metre you travel forward.

For now, just remember that an angle determines these ratios.  We will now look at another well-known rule about right-angled triangles.

Pythagoras’s Theorem

Pythagoras’s theorem – named after Pythagoras but probably known about four centuries beforehand, is usually taught as an algebraic rule that relates the side lengths of right-angled tringles.  You might remember this from school: if [latex]c[/latex] is the length of the hypotenuse and [latex]a[/latex] and [latex]b[/latex] are the lengths of the remains sides, then [latex]a^2+b^2=c^2[/latex].

For example, if [latex]a=4[/latex] and [latex]b=3[/latex] then we have:

[latex]\begin{align} c^2 &= a^2 + b^2 \\  c^2&= 3^2+4^2 \\ c^2&= 9+16 \\ c^2&= 25 \\ \sqrt{c^2} &=\sqrt{25} \\ c &= 5\end{align}[/latex]

If we didn’t know that a, b and c were side-lengths, we should remember that c could also have been -5 in this case.

Proof of Pythagoras’ theorem

As a rule, Pythagoras’s theorem is certainly one of the most useful that is directly applicable in “real-life” situations that we come across throughout our schooling. Algebraically we can solve for the third side whenever we have the two others (we can practice this later) but Pythagoras’s theorem also gives a number of opportunities for beautiful geometric and other mathematical proofs, which (unfortunately) sometimes aren’t introduced when taught in school.

Transcript

Pythagoras’s theorem in 3 dimensions

Let’s start with a problem.

Getting from a to b

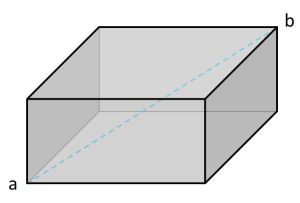1. Consider a rectangular polyhedron as shown.  What will be the length from the vertex [latex]a[/latex] to the opposite vertex [latex]b[/latex]? 2. How could you determine the height of a square pyramid from the length of its edges? 3. Could you find a way to work out the distance between any two points along the edge of the polyhedron (tip: Do you recall the notion of Cartesian Coordinates? What about if we think about coordinates in 3D?) Can you use Pythagoras’s theorem to make a general rule?

Perimeter and Area for triangles

Using Pythagoras’s theorem, we can now work out the perimeter of right-angled triangles provided we know two side-lengths.  We are also aware of the trigonometric ratios.  We can hence easily calculate perimeter in such cases, as well as area (since a right-angled triangle is just half a rectangle).  However there is also a formula for calculating the area of any triangle as long as we know the three side lengths.

This is Heron’s formula:

[latex]A=\sqrt{s(s-a)(s-b)(s-c)}[/latex]

where [latex]s=\frac{a+b+c}{2}[/latex].

It might be hard to see where this formula comes from, and it looks tricky to memorise, but in the following video, we can show some steps for working out an equivalent formula using algebra and a little problem solving.

Transcript

This example involves some tricky algebra – but it serves to show how we can often make deductions using things we already know in order to find unknowns. We know now that we can calculate (perhaps in a round about way), the area of any shape as long as we can break it down into triangles we know the lengths of. For polygons, this can usually be accomplished if we are given enough information, however it gets a little more difficult with circles.