11 Working with fractions
Many of us are out of practice with using fractions.
For many people, working with fractions goes into the category of ‘things I used to know how to do when I was 11 years old.’ We’re often taught fractions by being asked to memorise a series of rules, so it’s understandable if you can’t remember every one of them. If you’re already confident with addition, subtraction and multiplication using fractions feel free to skip this chapter.
Although fractions can seem less intuitive than other ways of representing the same numbers (which is easier to get a sense of: [latex]\frac{1163}{125}[/latex] or 9.304?), they can be very useful. If you find it confusing to work with fractions, this in turn will make it hard to work with algebra – so it’s worth spending some time to get the hang of them.
What are fractions?
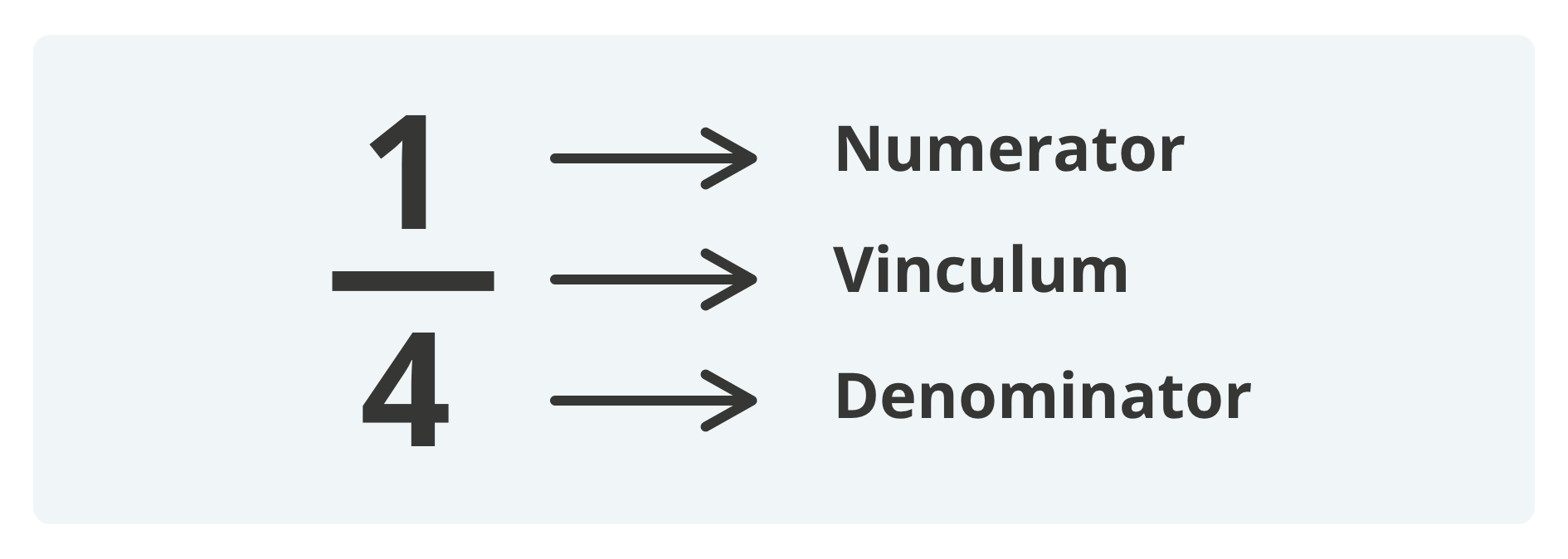
If you associate fractions with equally sized slices of cake, you’re probably not alone. You are probably familiar with terms like numerator and denominator. The vinculum is the little line that separates the top of the fraction from the bottom.
Fractions as parts of a single item
Most of us are taught, accurately, that fractions are equal parts of a whole. If you take a further step back, a fraction is ‘simply’ a division. In other words, one quarter is equal to one divided by four.
[latex]1\div 4=\frac{1}{4}[/latex]
This holds true no matter what the numbers in the numerator or denominator are. If the number on top is bigger than the number on the bottom then you have more than one whole thing. That is, if you had [latex]\frac{3}{2}[/latex] slices of pizza, you would have three halves of a pizza or one and a half pizzas.
Fractions represent divisions, but it’s also important to be aware that fractions are numbers. They can be placed on a number line, like any other number.
The division view of fractions
Another way to think about fractions is ‘the division view.’ In this way of understanding fractions, we start with whole items in the numerator and divide these whole items by the number in the denominator.
In this view, [latex]\frac{3}{4}[/latex] would mean we took three whole things and then divided all of them by four.
Common ways of representing quotients
A quotient is just another word for ‘division’ – so fractions, decimals, ratios and percentages are all quotients.
In most cases, it’s fine to convert between fractions, decimals and percentages. Just keep in mind they all represent the same number.
[latex]\frac{1}{5}=1:5=0.2=20 \%[/latex]
One fifth, 1:5, 0.2 and 20% are all equivalent figures and the way you choose to express them really comes down to the context you’re in.
If you are converting, note that in many cases decimals are imperfect approximations of fractions. For example, if you put [latex]1 \div 3[/latex] into a calculator, it will give you an imperfect approximation (0.3333…) whereas [latex]\frac{1}{3}[/latex] is precise.
Addition and subtraction
As students get older, they’re introduced to some more complex problems. These are the ones that can confuse many adults. Let’s look at perhaps the quintessential fractional problem that we encounter in our youths.
Have a go at the problem below. Don’t spend more than 15 minutes on it, though.
Pizza slices
 |
A whole pizza is sitting on the table.
You take [latex]\frac{1}{3}[/latex] of it, and your younger sister takes [latex]\frac{1}{4}[/latex] of it. How much pizza is left? |
This is an example of a problem that is routine for someone who is already familiar with the method, but can be quite tricky if we’ve forgotten how to do it.
You may have some intuition about this to begin with which we could use to set some limits – perhaps you might ‘guess’ that there’s somewhere between one half and one quarter of the pizza remaining.
If you struggled with this problem we recommend that you have a look online for some methods on adding and subtracting fractions – there are many good resources out there including Adding Fractions and Subtracting Fractions.
Multiplication
The next problem is another potentially routine one that essentially asks us to convert one fraction ([latex]\frac{km}{km/h}[/latex]) into another. This can be a tricky problem, and it might help if you know how to multiply and divide fractions. Have a go.
How long to the turn-off?
|
|
You’re driving down a highway.
At the moment you pass a street sign telling you that your turn-off is 15 km away, you are travelling at 100 km per hour. If you keep travelling at the same speed, how many minutes will it take you to reach the turn-off? |
One solution is presented below.
Entry
Let’s think about the entry phase for this problem. There are many ways that we could approach it.
As an example, I might draw the highway, figure out how far you would travel every minute, and then add them up until I get to 15 km (the picture might end up looking like a number line).
The main thing to contend with here – and this will probably be the key problem to overcome in any method – is one of conversion. How would I figure out how far I travel each minute, or how long it takes to travel a kilometre? In other words, how do I get from kilometres per hour to kilometres (or just metres) per minute?
Attack
I’m going to start by simplifying the problem to something I already know the answer to – that way I can easily test to see if my methodology works. Instead of travelling 15 kilometres, I’ll figure out how long it will take to travel 10 km at a steady speed of 100 km/h. The answer to this question is that it will take 6 minutes – here’s how I know:
- If I travelled one hour at 100 km/h, I would travel 100 kilometres. Similarly if I travelled half an hour, I would have travelled half the distance or 50 kilometres. Therefore, if I travel one tenth of an hour, I will travel one tenth of one hundred kilometres – which is 10 km.
- One tenth of an hour is [latex]\frac{60 \ minutes}{10}= 6 \ minutes[/latex]. So it seems logical to say it will take 6 minutes to travel 10 km.
So far so good – and to be honest at this point I can easily answer the question. If it takes 10 minutes to travel 6 kilometres, then it should take half that time to travel half that distance at the same speed. This means it would take 3 minutes to travel 5 kilometres. I want to travel 15 kilometres, so it should take 6+3=9 minutes to get there.
Generalising
That’s good, I have an answer that I’m fairly confident about. But that’s less interesting to me at this point than the main challenge – can I come up with a method that will work no matter what distance is being travelled?
Let’s see if I can use fractions and algebra to get to the same result. To recap on my strategy, I want to
- Find out what fraction of an hour it would take to travel a certain distance at a steady speed. That is, [latex]\frac{distance}{speed}[/latex].
- I then need to convert this fraction of an hour into minutes. 1 hour is 60 minutes, so I just need to multiply the fraction from step one by 60.
To set this out algebraically, I could use the letter [latex]t[/latex] to represent time and write the expression something like this:
[latex]t=\frac{distance}{speed} \times 60 \ min[/latex]
I am confident about my answers for the time it would take to travel 10 and 15 kilometres, so I’ll use these figures to test the equation out.
Let’s start with 10 kilometres – I’m confident the answer is 6 minutes.
[latex]\begin{align} t &= \frac{distance}{speed} \times 60 \ min \\ t &= \frac{10}{100} \times 60 \ min \\ t &= \frac{1}{10} \times 60 \ min \\ t &= \frac{60 \ min}{10} \\ t &= 6 \ min \end{align}[/latex]
Looks good. Let’s try 15 kilometres. It should take 9 minutes to travel 15 kilometres at 100 km/h.
[latex]\begin{align} t &= \frac{distance}{speed} \times 60 \ min \\ t &= \frac{15}{100} \times 60 \ min \\ t &= \frac{3}{20} \times 60 \ min \\ t &= \frac{3(60 \ min)}{20} \\ t &= \frac{180 \ min}{20} \\ t & = 9 \ min \end{align}[/latex]
And, just to be sure, let’s try to figure this method to figure out how long it takes to travel 150 kilometres – at 100 kh/h, I’m expecting the result to be 90 minutes (or 1.5 hours).
[latex]\begin{align} t &= \frac{distance}{speed} \times 60 \ min \\ t &= \frac{150}{100} \times 60 \ min \\ t &= \frac{3}{2} \times 60 \ min \\ t &= \frac{3(60 min)}{2} \\ t &= 90 \ min \end{align}[/latex]
Putting it all together
There are many real world problems where it can help to incorporate the addition/subtraction and multiplication/division of fractions. Have a go at the one below.
Flat packs
 |
You’re working at a factory warehouse.
You receive products in parts, which are then placed into flat packs and delivered to customers who assemble them. A new product comes in three parts, A, B and C. All three parts need to be delivered to the customer who ordered the item. The cardboard shipping boxes you use can each hold up to 10 kilograms of weight, which is enough for 3 lots of part A, or 4 lots of part B, or 6 lots of part C. If you receive an order for 10 items, what is the least number of boxes needed to ship them? |



