6 Algebra
Throughout this section, we’ll explore some of the fundamentals that can empower people to reason mathematically. We start with algebra.
When most of us think about algebra, we think about using letters or symbols such as [latex]x[/latex] or [latex]a[/latex] to represent variable quantities. When it comes to problem solving this is actually a pretty good place to start.
If we’d like to define it a little more tightly, algebraic expressions (eg, [latex]4x-7[/latex]) are a sequence of operations (like adding, multiplying, etc) performed on quantities and variables or unknowns. For example, the expression
[latex]3x+12[/latex]
means ‘start with a number, multiply it by 3 and then add 12,’ where [latex]x[/latex] represents the number we started with. You can choose any number to be [latex]x[/latex] and perform the sums on it, which is partly why we call it a variable.
So if [latex]x=2[/latex], then we have
[latex]\begin{align} & (3 \times 2) +12 \\ &= 6+12 \\ & = 18 \end{align}[/latex]
Isolating an unknown
In the scenarios above, we pick any number that makes sense (it could be almost at random) and then perform a series of operations on it. But one of the other things algebra can be really powerful for is figuring out an unknown number. Simple examples of this might be figuring out how much oil is left in a 44-gallon drum after a fraction of it has been removed, how much weight an iron girder can hold based on its density or guesstimating the amount of jelly beans in a jar based on its dimensions and the dimensions of a jelly bean.
That is to say, algebra is often used when we don’t really know what [latex]x[/latex] (or [latex]a,b,c...[/latex]) equals, but we’d like to find out.
Typically in these situations, we’ll have an equation, which differs to an ‘expression’ in that an equals sign will be involved. This can impose restrictions on some of the variables, which in turn can provide clues about what values they can take. For example, in the above, if we start out with an equation,
[latex]3x + 12 = 21[/latex]
Substituting 2 like we did before won’t allow both sides of the equality to stay the same. We then need to think about what has happened to the variable we’re trying to isolate and then reverse it. This is sometimes referred to as ‘solving for x’. It can be tricky at first but with a little practice it becomes second nature.
The main thing to remember when we do this is that anything we do, we have to do on both sides of the equation. This ensures both sides of the equation remain equal. A basic example will help: if [latex]3 \times 2=6[/latex], then [latex]3 \times 2 +2=6+2[/latex] or 8.
Let’s get classic and write it out like you’d find in a textbook, just to give an example (this is the ‘foundations’ section after all).
[latex]\frac{6x}{5}-2=8[/latex] – find the value of [latex]x[/latex]
I’ll set this out in a table so we can solve step-by-step:
| Here (right) is our equation which we need to evaluate or solve. | [latex]\frac{6x}{5}-2=8[/latex] |
| Now our task is to think about what is happening to [latex]x[/latex] and how we can reverse it.
We’ll start with the [latex]-2[/latex] first. There is no rule for where to start, but over time you will build your intuition for what makes the task most straight forward. Let’s reverse the minus 2 by adding 2. Remember we need to do it to both sides of the equations. |
[latex]\frac{6x}{5}-2+2=8+2 \\ \frac{6x}{5}=10[/latex] |
| Next let’s deal with the fact that [latex]x[/latex] is being divided by 5. To reverse this, we need to multiply both sides by 5. | [latex]\frac{6x}{5} \times 5=10 \times 5 \\ 6x=50[/latex] |
| And now there is only one operation left to deal with – let’s reverse the times 6 by dividing both sides by 6. | [latex]\frac{6x}{6}=\frac{50}{6} \\ x=\frac{50}{6}[/latex] |
| Finally, we want to ‘simplify’ this a little. In this case it could be written in a few different ways to make it a little more intuitive for a reader. | [latex]x=\frac{25}{3}[/latex] or [latex]x=8 \frac{1}{3}[/latex] or [latex]x=8.333...[/latex] |
Reverse order of operations
In the table above, we’ve used a method for solving often referred to as the reverse order of operations. Essentially, we’ve taken the normal order of operations and reversed it. Most of the time when we deal with an equation, we should leave addition and subtraction to the end – in this case we’ve reversed that order and ‘undone’ the subtraction first.
Performing the steps in this order is usually the best way to start when we solve equations – but we actually have some choice and could even use multiplication to remove the 5 from the left-hand side in the first step, as long as we make sure we apply the operation correctly to both sides.
In this case, we’d need to remember that the 5 multiplies both terms: the [latex]\frac{6x}{5}[/latex] as well as the [latex]-2[/latex]. It would give us
[latex]\frac{5(6x)}{5}=5 \times 8 \\ 6x-10=40[/latex]
And then we can proceed from here, ending up at the same result for x.
Problem
Let’s have a look at a classic routine problem to demonstrate how this works. You’ll probably remember that volume is calculated by multiplying length, width and height.
Fish tank factory
A small factory manufactures glass fish tanks. Each tank is made from a sheet of glass which is cut into sections. The factory always cuts squares from the edge, as it reuses these glass squares in other products that it manufactures. This is shown below.
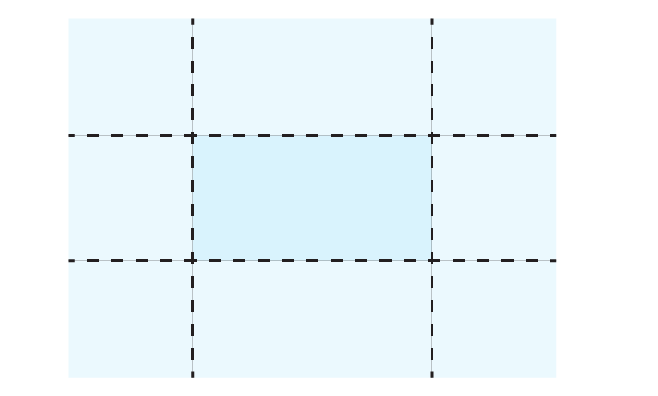 The edges are cut at a 45-degree angle and joined together flush using silicone. The left over squares are then removed.
The edges are cut at a 45-degree angle and joined together flush using silicone. The left over squares are then removed.
The sheet of glass that it is cut from is 1.4 meters long and 1.2 meter wide.
- The smallest tank that they manufacture is 30cm wide and 50 cm long. What is the maximum height of the fish tank, measured from the bottom to the top of the outside of the glass?
- If a tank must be at least 20 cm deep, what are the dimensions of the longest and widest fish tank the factory could manufacture? Would it be the same tank?
- Can you find an algebraic expression for the length of any rectangular tank manufactured using the same method and materials? What about its width or height?
This problem is loosely based on a problem from Stewart (2018).
A note on symbols for multiplication and division
It can take students a little bit of getting used to, but the [latex]\times[/latex] symbol is rarely used when doing algebra. This is to keep things concise and avoid confusion with letters (how could you tell what 4xx means?). If we are going to multiply numbers, like [latex]4 \times 3[/latex] then we could either include the multiplication symbol or use brackets. If we use brackets, we assume that a quantity outside a bracket is multiplied by a quantity within a bracket – eg both [latex]4 \times 3=12[/latex] and [latex]4(3)=12[/latex] represent the same operation.
It’s also unusual to see the symbol for division [latex]÷[/latex] in an algebraic expression. We usually use fractions such as [latex]\frac{3}{5}[/latex] and if we’re trying to set things out on the same line we can also just use [latex]3/5[/latex]. It’s also common to see these written as decimals such as [latex]0.6[/latex] in certain contexts or situations.
Implied brackets
We need to be careful with ‘implied’ or invisible brackets. When we have an expression like [latex]\frac{7x+2}{3-x}[/latex] this means that we have a number ‘x’ which we multiply by 7, add 2, and then we take the result and divide it by three minus the same number ‘x.’ So there are implied brackets both above and below the separating line (the vinculum): brackets around the [latex]7x+2[/latex] and around the [latex]3-x[/latex].
Common words, symbols and expressions
Here are some common ways to represent mathematical operations.
| Common words | Common symbols or expressions |
| Addition, sum, add, total, plus | [latex]x+y[/latex] |
| Subtraction, subtract, minus, less, difference, decrease, take away, deduct | [latex]x-y[/latex] |
| Multiplication, multiply, product, by, times, lots of | [latex]xy, x(y), x×y, x\cdot y[/latex] |
| Division, divide, quotient, goes into | [latex]\frac{x}{y}, x÷y, x/y[/latex] |
Painters and shopkeepers
Head back to Chapter 4 to take a look at the problems.
- For the Painters problem, are you able to determine expressions and come up with a general solution for when Alma paints a house in A hours and Marvin paints a house in B hours?
- How can the Shopkeeper problem be set up algebraically?
Quiz
References
Stewart (2018). Single variable calculus : concepts and contexts (Fourth enhanced edition.). Cengage.


