39 Minimum spanning trees
The areas of Graph Theory and Topology are huge – mathematicians can spend their lives devoted to working on specific sets of problems.
We’ll now look at a couple of common problems, how to represent them with graphs, and how to solve them. The first is the problem of finding a minimum spanning tree.
A tree in graph theory is usually defined as a connected graph with no cycles. Recall that when we think of cycles, we don’t usually allow back-tracking. We could also think of trees as connected graphs with only one face (the “outside” region). There’s even the concept of a forest in graph theory – but we won’t consider these.
A spanning tree is a special type of subgraph, which means that we need a graph to start with – we can’t just say that a graph is a ‘spanning tree’ without referring to that original starting graph. Starting with any graph, a subgraph is a graph that can be constructed using any of its existing edges and vertices (see figure below). If we include an edge, we need to make sure that the vertices connected by that edge are included too.
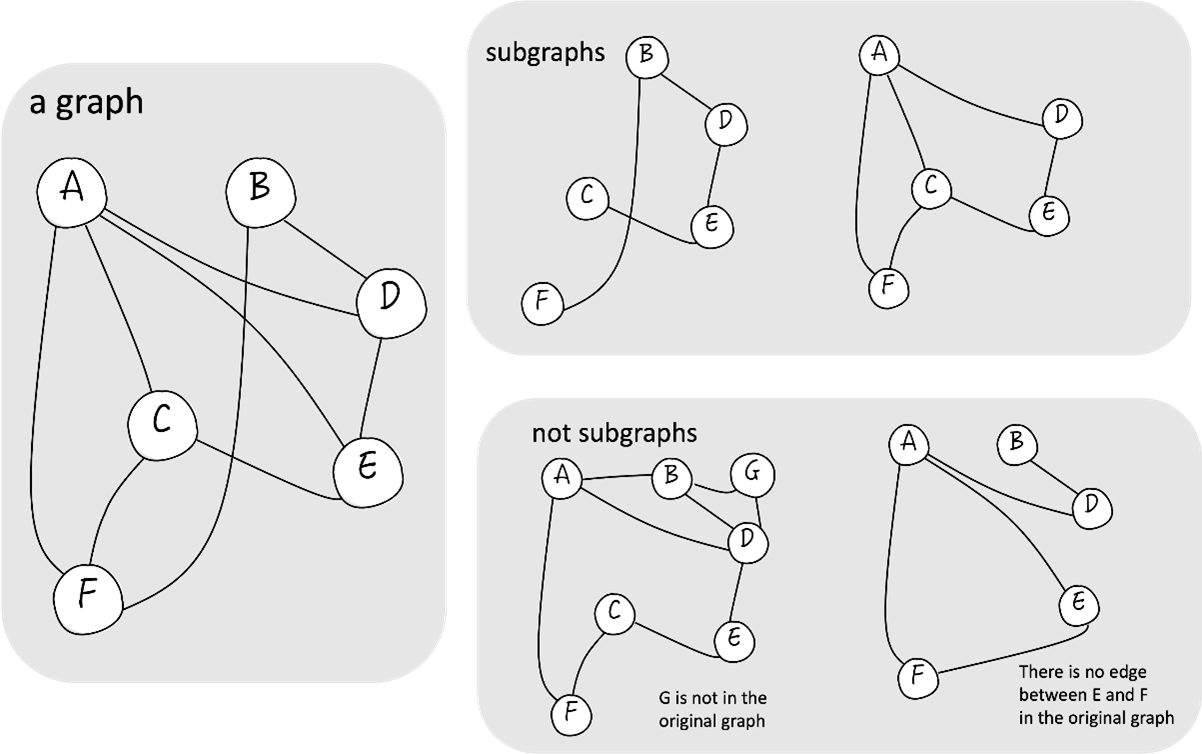
So now, we can define a spanning tree as a subgraph that includes all vertices of the original graph and is also a tree.
In applications like what was shown in the video, we are interested in finding the minimum spanning tree, where the aim is to find a spanning tree that minimises the sum of edge weights.
Minimum spanning trees
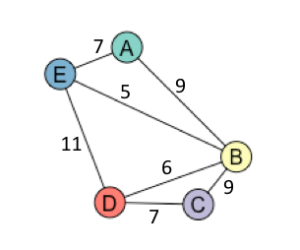
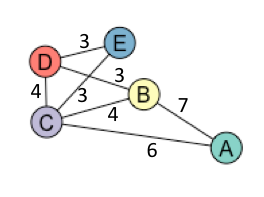
Can you determine the minimum spanning trees of these graphs?
Can you come up with a method of determining the minimum spanning tree of any graph, no matter the weighting or number of edges and vertices?
 |
 |
Useful algorithms
Once the number of edges and vertices grows large, it becomes harder to be sure that the spanning tree we find has the smallest weights possible. We need to approach the selection of the edges logically and methodically. Here are two potential algorithms that might help us achieve this. Both begin with a graph as an input, and output the minimum spanning tree of that graph.
| Algorithm 1: Build from the least expensive | Algorithm 2: Eliminate from most expensive. |
After following this sequence you should be left with a spanning tree. |
After following this sequence you should be left with a spanning tree. |
Algorithm 1 is also known as “Kruskal’s Algorithm” and was first published by Kruskal (1956). Algorithm 2 was also proposed by Kruskal in the same paper, but is more commonly referred to as the “Reverse-delete algorithm“.
The video shows these algorithms in action.
Generalise
 |
How many edges will there be in a tree (with respect to the number of vertices?) |
References
Kruskal, J. B. 1956. On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical Society. 7 (1): 48–50. doi:10.1090/S0002-9939-1956-0078686-7.


