30 Volume
For volume, we are essentially extending the idea of area, except now we are considering the area for each step in height.
It might not seem obvious, but if the cross-sectional area is the same for any two shapes, then solids made by extending them upward will have the same volume too.
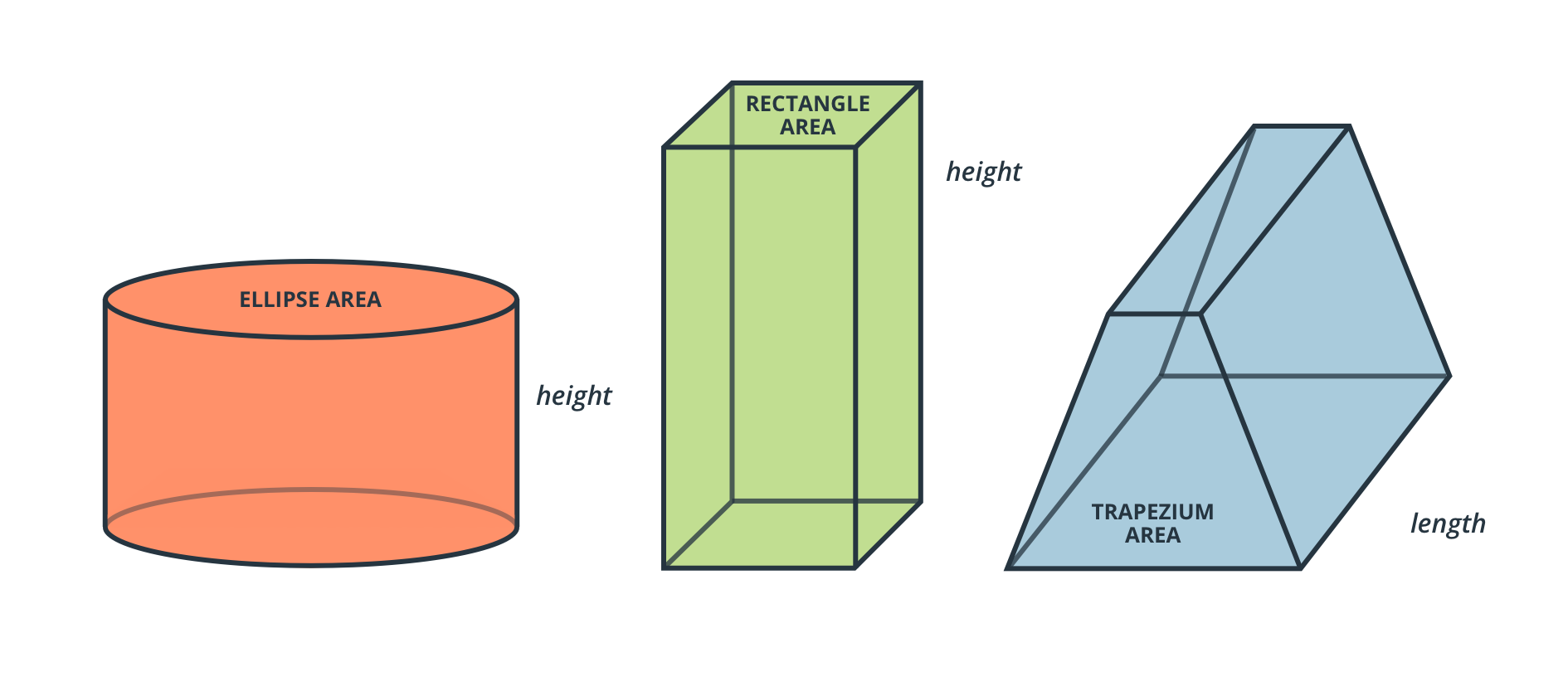
However there are some special shapes, too, such as cones and pyramids, which gradually get smaller as their size increases.
Determining the volume of a pyramid
 |
Determining the volume of a pyramidA stepped pyramid, with five layers, has a base length of 50 metres. Each layer decreases at a uniform rate, and the length of the top layer has a length of 5 metres.. Can you figure out a method for determining its volume?
What if it had a straight, sloping edge rather than steps? |
Once you’ve had a go at the activity above, take a look at the solution offered in the video below.
Quiz
Have a go at the following quiz which gives practice for working out volumes.
Notes
Using the tool below, create a brief description of the formula for calculations that we have covered so far this week (plus the volume of a sphere).
Include an example with some reasoning about where the formula “comes from”. If there are steps you’re not sure of, check back over the week and update accordingly. Try to make your explanation as simple as possible.
If it’s too tricky (explaining the area of a sphere can be pretty difficult), think of a way you might be able to remember it and differentiate it from different formulas.
Warning: the text input into the app below will not save if you close your browser or navigate away from the page. Please export your text to keep a copy.


