40 Graph colouring and chromatic numbers

If you had to give every vertex that shared a connection a different colour, how many colours would you need?
Another important problem in graph theory is that of finding the chromatic number of graph – or the minimum number of colours required to assign a colour to every vertex such that no adjacent vertices are the same color.
Although the problem of the chromatic number arose from colouring maps, it can actually be applied to quite different problems and situations. Suppose we have a number of fish, and we have some knowledge about whether some of the fish eat the other ones, or shouldn’t be kept in the same tank. Well the chromatic number tells us how many tanks we need so that we can keep the fish away from their predators, and the colouring tells us how to assign those fish to the different tanks.
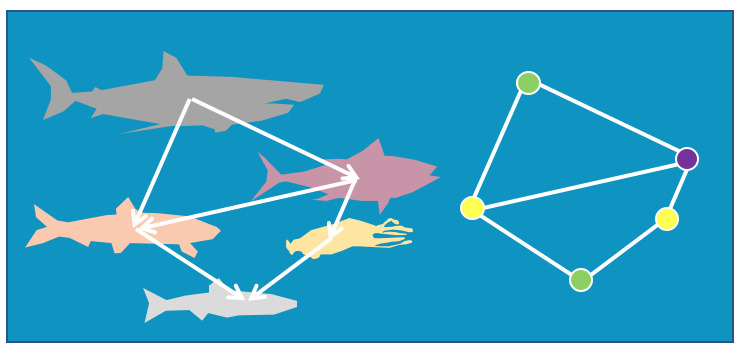
However, it can be difficult to find an optimal colouring of a graph. Once a graph is large enough, we could proceed in colouring from vertex to vertex but not be quite sure whether we’ve done it in the best way or not. Fortunately, there’s an algorithm that can give us a systematic way of proceeding. It isn’t guaranteed to obtain the best colouring, but it is usually pretty good, and provides us with another example of where a solution method is described as an algorithm rather than a rule (Welsh and Powell, 1967).
The Welsh-Powell Algorithm
Input: A graph
Output: A colouring of the graph that should be close to optimal
Step 1. Order the vertices of the graph according to their degree in decreasing order.
Step 2. For each colour in {Colour 1, Colour 2, Colour 3…}, proceed through each of the vertices in order, if the vertex hasn’t been coloured yet and it is not adjacent to a vertex of the colour you’re using, assign that colour, otherwise move onto the next vertex. Once you’ve run out of vertices, move to the next colour and start again.
You should end up with a complete graph colouring. The number of colours you used should be the chromatic number.
Applying the algorithm
See if you can apply the Welsh-Powell algorithm for the following graphs to find an optimal colouring.
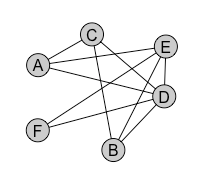 |
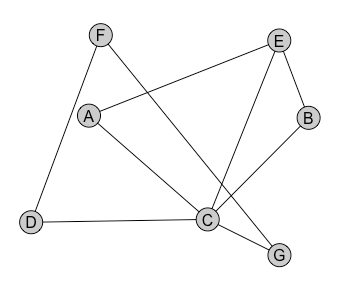 |
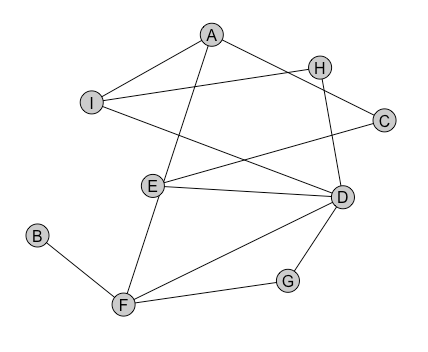 |
Watch this online video for an example of applying the Wesh-Powell algorithm, once you’ve had a go for yourself. Take a look at some more worked examples, too, if you’re interested.
References
Welsh, D. J. A. and Powell, M. B. 1967. An upper bound for the chromatic number of a graph and its application to timetabling problems, The Computer Journal. 10 (1): 85–86. doi: 10.1093/comjnl/10.1.85

