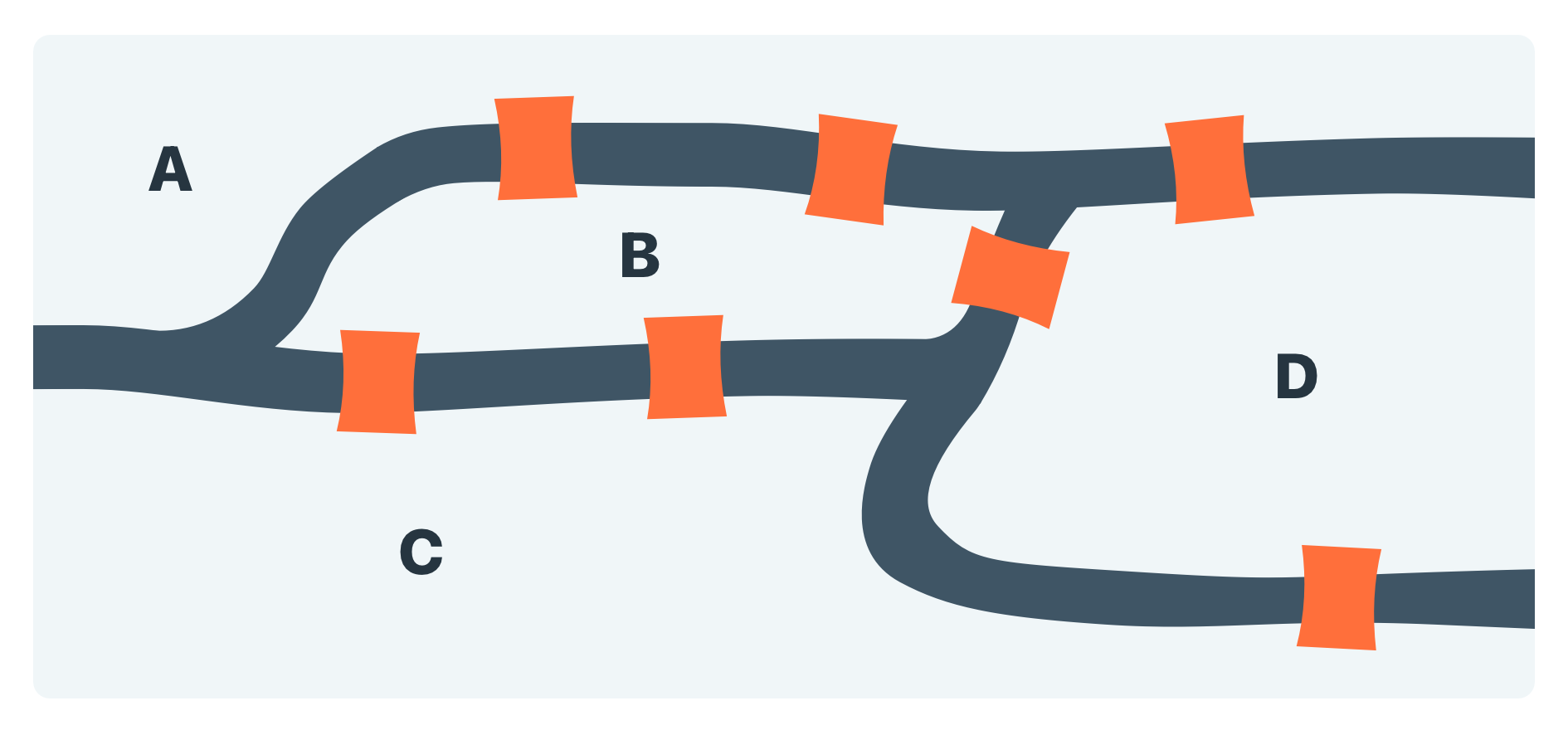
36 Graphs and networks

In this topic we look at some mathematical results pertaining to networks and graphs.

The term ‘graph’ here is a specialised term for a mathematical representation of relationships consisting of nodes and edges, rather than the way it is commonly used to just mean a diagram or a plot with axes.  What we look at here also represents the starting point for topology, which can roughly be described as the mathematical study of whether or not things are ‘close’ or connected.

Throughout the topic, you’ll learn how to solve routine problems using Eular paths, Eular cycles, mimimum spanning trees and graph colouring.

Let’s start with one of the classic problems in the discipline of topology: the Königsberg bridge.

The Königsberg bridge

This problem is a good reminded that sometimes it’s impossible to achieve the goal of the problem.  In these cases, it’s left for us not to ‘answer’ the question, but instead to show that it’s impossible.

Let’s take a look at the problem.

Transcript

Or if you’d prefer a written expression of the problem:

The Königsberg bridge

The image below represents a map of the bridges of the city of Königsberg in the 1800s. How could someone walk through this city, crossing each bridge once and only once? Remember the entry, attack and reflection phases as you work through the problem. If you enjoy the problem, there are several more topological problems developed using Mathigon.

In case we hadn’t made it clear enough already, there is no way to cross each bridge once and only once.  However, attempting to solve the problem can still help us develop valuable insights and methodologies.  The video below shows some potential methodologies for attempting to solve the problem.

Transcript

Recall that often in problem solving, the problem is not the real problem. A very limited number of people would actually care about whether or not it is possible to take a walk in Königsberg without recrossing a bridge, what we really care about is whether there are any general results that seem to apply in this framework. Which arrangements of bridges and regions will allow us to determine such a path? Is there a way we can tell quickly?

Let’s practice the important process of generalising, to see if we can get a good feel for what’s involved in problems of this kind.

Generalising from the Königsberg bridge problem

What are the important aspects of the Königsberg problem that make it impossible to find this kind of walk? Use some problem solving strategies to reflect: e.g. can you add a bridge that makes it possible to find the walk? Could you move a bridge that makes it possible to find a walk? Could you remove one bridge? How does the important information change with each setup?