37 Graph theory
 Let’s start with some terminology
Let’s start with some terminology
The video will give you a good overview of some of the terminology we’ll use over the week.
Let’s start with a graph. A graph, in the context of ‘Graph theory,’ is a figure made up of points (referred to as nodes or vertices) connected by lines (arcs or edges).
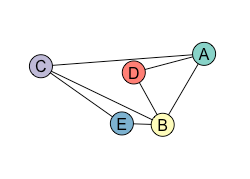
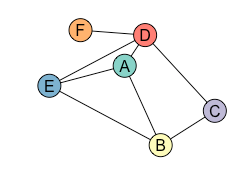
The left graph has 5 vertices, 7 edges and 4 ‘faces’ (the regions enclosed by BCE, ABD, ACBD and the outside region counts too). The graph on the right has 6 vertices, 8 edges and 4 faces.
As mentioned in the introductory video, a key idea that differentiates graph theory from geometry is that often the actual position of a node, or the length of an arc is meaningless. The following graphs could both be used for representing the situation in the Königsberg bridge problem.
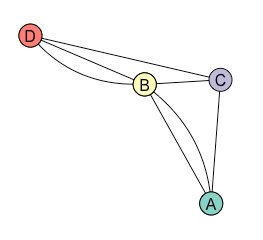
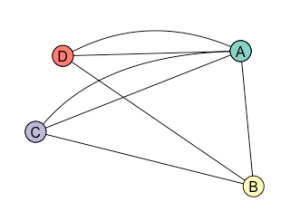
Even the labelling doesn’t particularly matter – we just need to represent the middle region as a vertex, connecting twice to the vertices representing the upper and lower regions, then the remaining vertex (representing the right-most region) should connect once to each region.
The ‘degree’ is the number of edges going into or out of a vertex. In the graph below, the degree of vertex A is 3 and the degree of vertex B is 7.
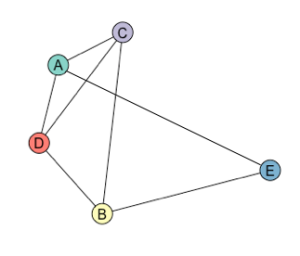
We can also count faces – as long as it’s a graph that can be layed out so that no edges are crossing over one another (if it’s possible, such graphs are said to be ‘planar‘.)
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 |
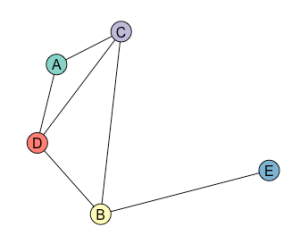
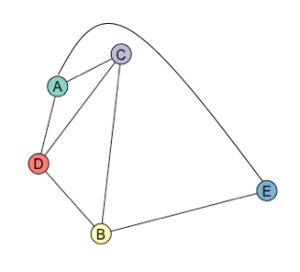
It’s hard to work out the number of faces from figure 1 because the line AE crosses some of the other edges. If we remove this line (figure 2) and redraw it so that it doesn’t cross any edges (figure 3), we can then see that it has 4 faces – the regions enclosed by ACD, BCD, ACBE, and the region outside.
More important terms
- A path – a sequence of edges that may connect two vertices.
- A cycle (or sometimes ‘circuit‘) – is a path that starts and finishes from the same vertex, usually not allowing backtracking (e.g. a path ADA in the above 3 graphs would not usually be considered a cycle)
- Connected – a graph is connected if there is a path from any vertex to any other vertex in the graph
- Isomorphic graphs – two graphs are isomorphic if they have the same number of vertices and if the edges correspond exactly. Usually this is independent of the labelling – but a common way of describing isomorphisms is that one graph can be obtained from the other by a continuous “morphing” – moving of the vertices and/or bending of the arcs.
Planar graph
 |
Can you draw a connected planar graph with 6 vertices and 8 edges?
How many faces does it have? Is it possible to draw it differently so that it has fewer or more faces? |

