2 Entry

Mathematical problems can usually be approached a number of ways, and require more than just an answer.
Broadly speaking, mathematical problem solving involves the application of logical and mathematical methods to non-routine or open problems.
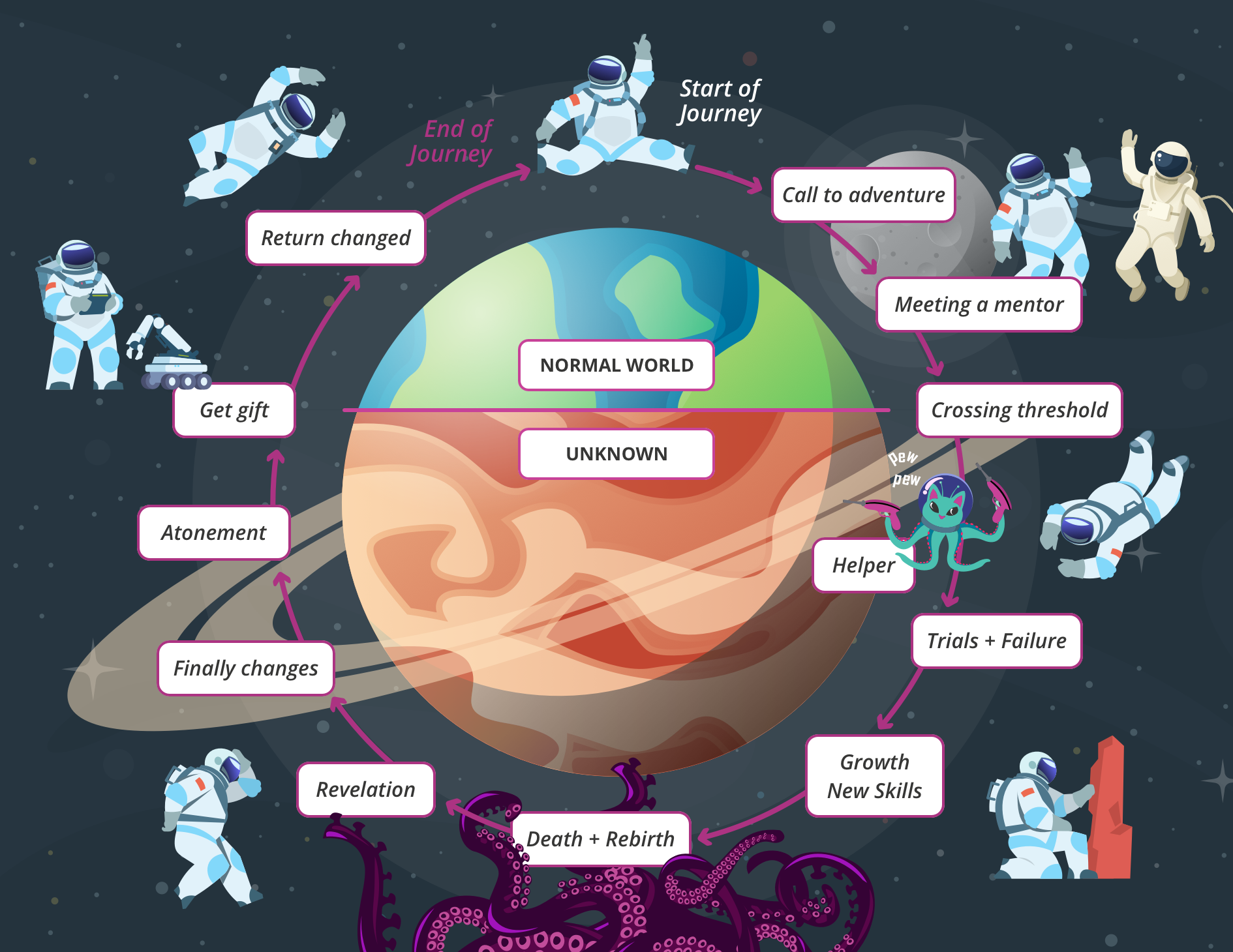
A number of formal frameworks have been identified for undertaking a problem solving task, sometimes with 9 steps, sometimes with 5, however we follow Mason, Burton and Stacey (2010) in reducing them to three phases: Entry, Attack and Review. In terms of our Hero’s Journey analogy, the breakup looks something like this.
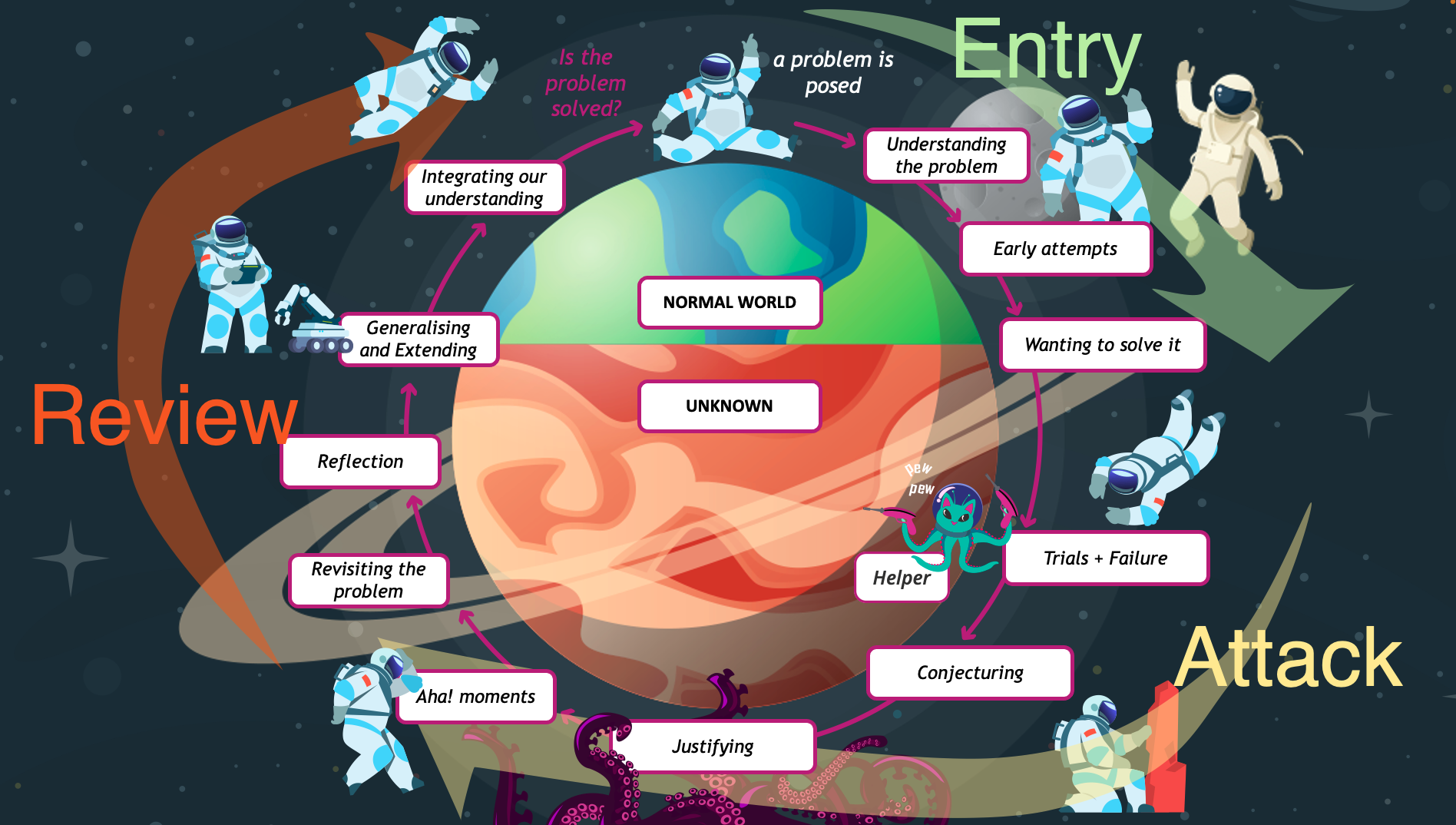
Entry: taking up the call
In the entry stage, we usually try to identify the important features of the problem, the information we require, how we interpret the problem, whether the problem is similar to something we have seen before. The video below explores the idea a little more.
Let’s practice using the entry phase.
The Huashan problem

In China there is a mountain called Huashan that has a plank walk on the side of a cliff.
There is one section where there are only 7 foot and hand holes (each pair can hold just one person). There are three people trying to go from left to right, and three trying to go from right to left. One person can jump across someone going the opposite direction or move across one space if there is a free hand hole. What is the minimum number of moves that can be made to so that the blue climbers occupy the three spaces on the left and the red climbers occupy the three spaces on the right?
Without trying to solve the problem, have a go at the entry phase for the problem below (don’t try to solve it – just see if you can answer the “I know…”, “I want…”, and the “What Can I Introduce?” aspects).
This problem is based on Leapfrogs from Mason, Burton and Stacey (2010, p 62).
Did you get stuck in starting? Remember that a great way to start is to specialise. Write down your thoughts so far under the headings:
- I know…
- I want…
- What can I introduce?
Now you can either spend some time trying to solve it, or watch this video and see if your entry was similar or different.
References
Mason, J., Burton, L. and Stacey, K., 2010. Thinking Mathematically Second Edition. England: Pearson Education Limited.
A non-routine problem is a problem which invites multiple methods to solve, and potentially more than one solution may be acceptable.
They differ from a standard textbook maths problem in that they are not designed to be solved by using a pre-specified method, and do not necessarily have an answer that can be predetermined.

