29 Circles

Mathematicians tried for centuries to figure out how to determine the length of a circle based on its radius or diameter.

Many methods for calculation were investigated, but a simple rule eluded them because the relationship needed to be described in terms of a new type of number, i.e. the irrational number [latex]π[/latex] (pi). Today, we recognize [latex]π[/latex] as the ratio of a circle’s circumference to its diameter, equal to a value close to 3, but as you might recall, it’s not a rational number (i.e. it can’t be expressed as the ratio between two whole numbers). Pi was approximated to high degrees of accuracy, even thousands of years ago, and today we have the technology and computing power to express it to millions of decimal places of precision.

Let’s take a look at how we can use a similar technique in Scratch to approximate [latex]\pi[/latex].

Transcript

Running track

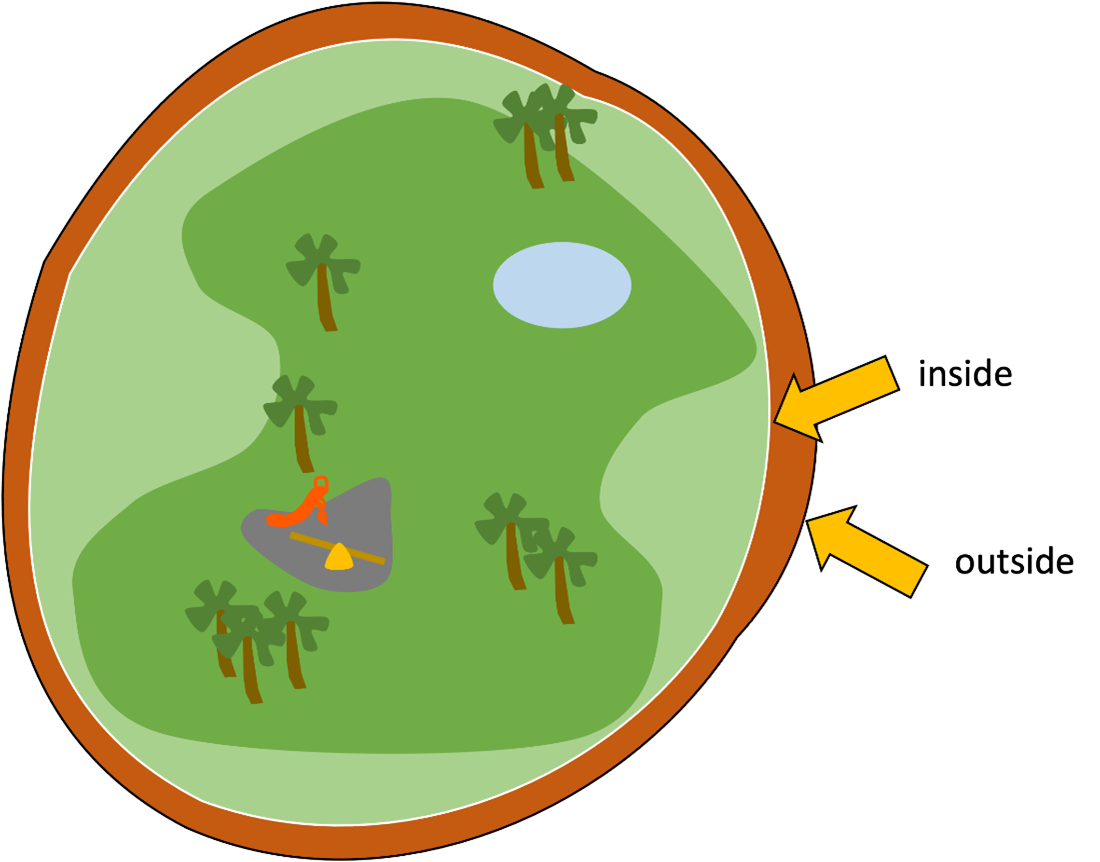There is a running track that goes around your local park that’s meant to be 1km for one lap, however if we assume the track is roughly circular, you might be covering more or less than 1km depending on whether you’re running on the inside or outside of the track.  What would be the difference if the track width is about 1.5m?

Area of a circle

We might all now be well aware of the formula for determining the area of a circle: [latex]A=\pi r^2[/latex].  However, it, too, can be a difficult thing to calculate with precision.  To see how we can use [latex]\pi[/latex] to approximate the area of a circle, it helps to think of the area of a circle in terms of triangles.  The video below explains.

Transcript