12 What is an algorithm?

An algorithm is just a list of instructions for a computer.
As the video says, what makes them different from instructions from Ikea is that we can use them to help solve general problems (like ‘what are the prime numbers under a million?’) as well as specific ones. Take a look at this video that gives a good definition.
Stop and think
Suppose you have the set of numbers: 3, 6, 10, 20, 7, 49, 2, 5, 20; what would be a set of instructions to determine the highest number? Which operations would the computer need to understand and what else would be required?
Have a look at the video below for one solution once you’ve spent a few minutes thinking about it.
Input through to output
If the algorithm we have is designed to solve a problem, then often this solution will depend on the particular case or situation, and the algorithm will take this information into account. We can refer to this broadly as the input to the algorithm. So in the case of determining primeness, we would need to know which number the algorithm will be checking, while determining the largest number will depend on a list of numbers, and counting the number of people in the room will depend on the room we’re looking at.
We also need to know what the solution is, and so usually this is the output. Like the input, the output could be one number or a set of numbers, or something even more general. Of course, if we think of the sequential process a computer might go through to give us this output, we usually need a stopping condition. In some cases, the stopping condition will just be when the algorithm finishes the list of instructions, however sometimes the actual number of steps the algorithm takes may be unknown.
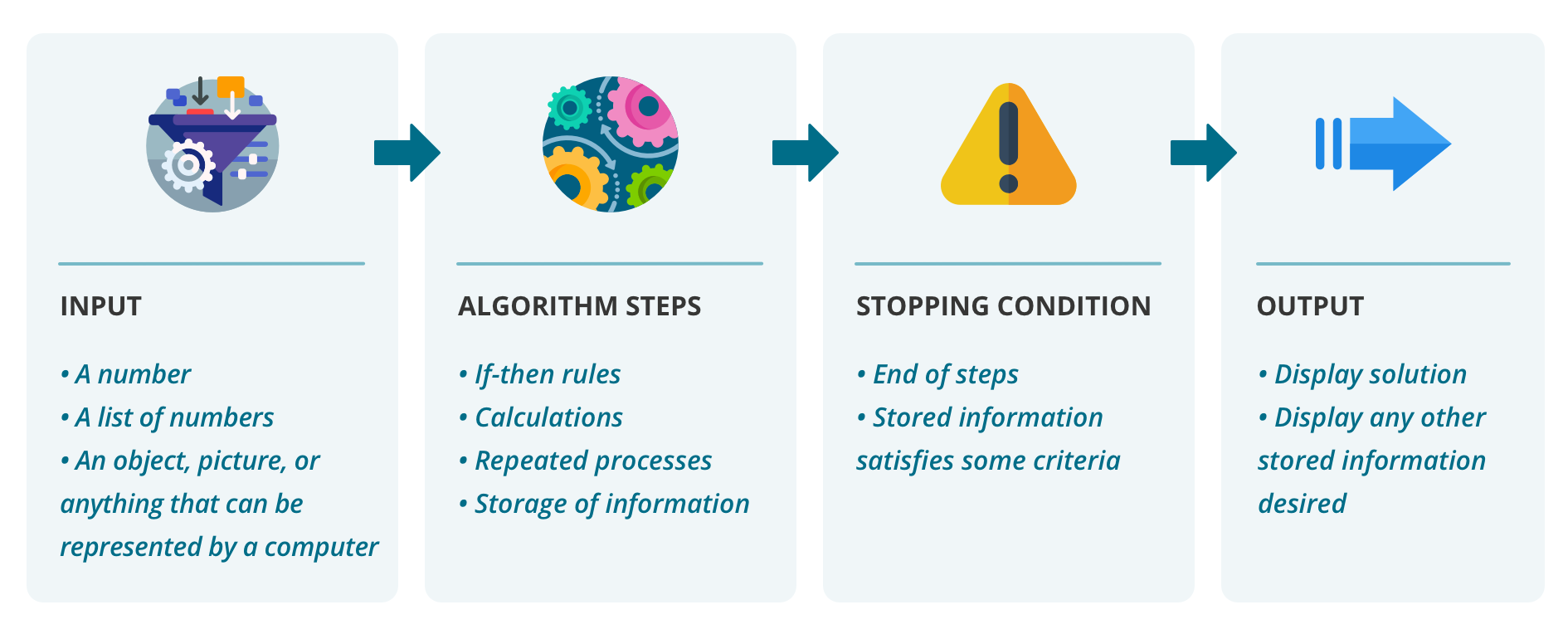
Download accessible version of algorithm diagram
The Collatz Conjecture
The Collatz conjecture is another great example of a simply stated problem that is very difficult to solve. Let’s suppose we have a positive integer to start with. Then, if the number is even, we divide it by 2, otherwise, we multiply it by 3 and add 1. We keep doing this, and the conjecture states that no matter what number we start with, we will end up with 1.
7 is not even, so we multiply by 3 which gives us 21 and add 1. So now we have 22.
22 is even, so we divide it by 2, to give 11.
11 is not even so we multiply it by 3 to get 33, and add 1. We now have 34.
Does it feel like this will end up approaching 1? Use the Scratch program below to explore the conjecture – when you enter a number, it will give you the sequence of values until it reaches 1. It will also plot the points on a graph (although it’s only set up to plot numbers under 150 or so).
The Scratch program implements the algorithm from the Collatz conjecture and allows us to specialise and look for patterns without having to do all the calculations. What are some smaller conjectures you can make based on the numbers you’ve tried? This is considered such an interesting problem, archetypical to the field of computer science, that it adorns the exterior of the Warsaw University Library (among texts in different languages, science and statistics formulae and sheet music).
Your first algorithm
Can you remember how to tell if a number is prime or not? Have a look at Simon’s video above, and this method if you’ve forgotten.
See if you can write clear “algorithmic” instructions to check whether an input, n is prime. You don’t need to write the specific code, but make sure you have a logical order of steps and include a consideration about which steps would require special operations that would need to be understood by a computer.
For example, to check divisibility, we can quickly check divisibility ourselves by using a calculator: if n divided by 3 gives a whole number result, then we know n is divisible by 3 – if implementing this idea on a computer, we’d need some way for the computer to know that n divided by 3 is a whole number, or just some operation that is able to say that n is divisible by 3 is a true or false statement.

