Topic 2: The Risk and Return Trade Off in Financial Decision Making
Introduction
The risk-return trade-off is a fundamental concept in finance, emphasizing that higher returns often come with higher risks. Financial managers must evaluate this balance when making decisions, ensuring that potential rewards justify the associated risks. This principle applies in almost every financial decision faced by financial managers.
A real-world example of the risk-return trade-off can be seen in Qantas Airways during the COVID-19 pandemic. The airline faced a significant decline in revenue and had to decide whether to scale back operations or invest in fleet upgrades to prepare for post-pandemic recovery. Scaling back posed lower financial risk but limited potential returns, while investing in fleet renewal was a riskier decision with higher potential for long-term growth. Ultimately, Qantas chose a balanced approach—reducing costs in the short term while continuing investments in key areas to remain competitive.
This example highlights how financial decision-making requires careful evaluation of risk and return. In this topic, you’ll delve deeper into these concepts, exploring how to measure risk and return, the benefits of diversification, and advanced tools like the Capital Asset Pricing Model (CAPM) and decision-making frameworks for uncertain scenarios. Understanding the risk-return trade-off equips you with the skills to navigate complex financial decisions confidently.
The key learning outcomes for this topic include:
- Analyze the Risk and Return of a Single Asset: Evaluate the expected return and associated risk of individual financial assets using appropriate measures.
- Understand Diversification and Portfolio Risk and Return: Explain how diversification reduces risk and calculate the risk and return of a portfolio comprising multiple assets.
- Apply the Capital Asset Pricing Model (CAPM): Use the CAPM to assess the relationship between risk and expected return and determine the cost of equity for an investment.
- Make Decisions Under Uncertainty: Apply decision-making frameworks to evaluate financial outcomes in uncertain scenarios and identify the optimal course of action.
Learning Objective 1: The Risk and Return of a Single Asset
In finance, risk and return are two interconnected concepts that form the foundation of financial decision-making. Risk refers to the uncertainty or variability of outcomes, particularly the potential for loss, while return represents the gain or benefit earned from an investment or decision. The relationship between risk and return is crucial: typically, higher returns are associated with higher risks, reflecting the compensation investors or firms require for taking on greater uncertainty.
For a single asset or investment, return is typically calculated as the percentage change in the asset's value over a period, including any income generated (e.g., dividends or interest). Risk is measured using statistical tools such as the standard deviation of returns, which quantifies the variability of returns over time.
1.1 Measures of return
Return represents the net gain or loss in dollar terms from an investment over a specified time period. When referred to as the rate of return, it is expressed as a percentage of the investment's initial cost. The rate of return is calculated by measuring the percentage change in the investment's value from the beginning of the period to the end.
- Dollar returns
Dollar return, also known as absolute return, is the net monetary gain or loss from an investment, calculated as the difference between the ending value of the investment and its initial cost, including any income earned.
Total dollar return = income from investment + capital gain (loss) due to change in price/value of the investment
For example, if you bought a bond for $950 one year ago and received two coupon payments of $30 each. Your total dollar return can be calculated as below assuming that you can sell the bond for $975 today.
Income = $30 + $30 = $60
Capital gain = $975 – $950 = $25
Total dollar return = $60 + $25 = $85
- Percentage returns
It is more common to express return as a percentage because it provides a standardized measure that allows for easy comparison across different investments, regardless of their size or initial value. Percentage returns normalize the gains or losses, making it possible to evaluate the performance of investments with varying dollar amounts on a consistent scale.
For example, a 10% return on a $1,000 investment represents the same relative performance as a 10% return on a $10,000 investment. This consistency is particularly useful for comparing options, analyzing trends, and communicating investment outcomes effectively.
Accordingly, from this point onwards, we only focus on the calculation of percentage return.
- Holding period returns
A holding period return is the total percentage return earned on an investment over the entire period it is held, including both capital gains and any income received during that time.
Example: Calculating Holding Period Returns
You bought a share for $35 in 2015, and you received dividends totalling $1.25. The share is now selling for $40 in 2022.
| 2.1 | Holding period return (Discrete compounding) | [latex]R_T=R_{CA}+R_I=\frac{P_1-P_0}{P_0}+\frac{{CF}_1}{P_0}[/latex] |
The holding period return over the 7-year period is
Dividend yield = $1.25 / $35 = 3.57%
Capital gains yield = ($40 – $35) / $35 = 14.29%
Total holding period return = 3.57% + 14.29% = 17.86%
Alternatively, the total holding period return can be calculated using total dollar returns as below
Total holding period return = ($1.25 + $5)/ $35 = 17.86%
Note that holding period return is the return over an investment horizon and therefore is not an annual return.
- Expected returns
Unlike the holding period return which is a backward-looking measure that reflects the actual percentage return earned on an investment during a specific period, expected return is the anticipated average return on an investment based on probabilities of various outcomes. It is calculated as the weighted average of possible returns, with each return multiplied by its likelihood of occurrence. Expected return provides a forward-looking estimate, helping investors assess potential performance and compare investments under uncertainty.
| 2.2 | Expected return on an asset (Probability given) | [latex]{E(R}_{Asset})=\sum_{i=1}^{n}{(p_i\times R_i)}[/latex] |
Suppose you have predicted the following returns for shares A and B in three possible states of the economy. What are the expected returns?
|
State |
Probability |
A |
B |
|
Boom |
0.3 |
0.15 |
0.25 |
|
Normal |
0.5 |
0.10 |
0.20 |
|
Recession |
0.2 |
0.02 |
0.01 |
The expected return of share A and B can be calculated as:
E(A)=9.9%=0.3*0.15+0.5*0.10+0.2*0.02
E(B)=17.7%=0.3*0.25+0.5*0.20+0.2*0.01
When the probability of each outcome is the same, the 'expected' return is the same as the 'average' return.
| 2.3 | Expected return on an asset (number of periods/equal probability is given) | [latex]{E(R}_{Asset})=\frac{\sum_{i=1}^{n}R_i}{n}[/latex] |
If the frequency of your return is not annual, you will need to annualise the expected return so that you can compare the performance of different securities available in the market. For example, an average monthly return can be annualized by multiplying the average monthly return by 12 (12 months in a year).
1.2 Measures of risk
Risk in finance refers to the uncertainty associated with the potential outcomes of an investment, particularly the possibility of earning less than expected or incurring a loss. It is a key consideration in financial decision-making, as higher risk is often associated with the potential for higher returns. In finance, risk is commonly measured using statistical tools such as variance and standard deviation, which quantify the variability of returns around their average. These measures help investors and financial managers assess the likelihood and magnitude of potential deviations from expected returns, enabling informed decision-making.
- Variance
Variance is a statistical measure that quantifies the spread or dispersion of a set of data points, particularly how much individual values deviate from the mean (average) of the dataset. Using the example of Share A and B above, let's illustrate how variance can be estimated when probabilities of future outcomes are given.
| 2.4 | Variance of return on an asset (Probability Given) | [latex]Var(R)=\sigma_R^2=\sum_{i=1}^{n}\left\{(p_i\times\left[R_i-E(R)\right]^2\right\}[/latex] |
Variance of A= 0.3*(0.15 – 0.099)2 + 0.5*(0.10 – 0.099)2 + 0.2*(0.02 – 0.099)2 = 0.00209
Variance of B = 0.3*(0.25 – 0.177)2 + 0.5*(0.20 – 0.177)2 + 0.2*(0.01 – 0.177)2 = 0.007441
When you work with historical data such as past returns on an asset, how the variance of the returns is calculated depends on whether you have a population or a sample of returns.
- A population includes all possible data points in a dataset. For example, if you're analyzing the returns of a stock over its entire history, you're working with the population.
- A sample is a subset of the population, used when it’s impractical or impossible to collect data for the entire population. For instance, if you analyze the stock’s returns over the past five years instead of its full history, you're working with a sample.
The key difference is the denominator in the variance formula. It is N (total number of data points) for a population and n-1 (where n is the sample size) for a sample.
| Population Variance: [latex]Var\left(R\right)=\sigma_R^2=\frac{\sum_{i=1}^{n}\left[R_i-E\left(R\right)\right]^2}{n}[/latex] | ||
| 2.5 | Variance of return on an asset | |
| Sample Variance: [latex]Var\left(R\right)=\sigma_R^2=\frac{\sum_{i=1}^{n}\left[R_i-E\left(R\right)\right]^2}{n-1}[/latex] |
- Standard Deviation
Apart from variance, standard deviation is another measure of risk. It is simply the square root of variance. It is easier and more intuitive to interpret than variance because it is measured in the same unit as the return (%) whereas variance is expressed in squared units (for example square percentage returns).
Equation 2.6 showcases how standard deviation of returns is computed.
| 2.6 | Standard Deviation | [latex]StDev\left(R\right)=\sqrt{Var\left(R\right)}=\sqrt{\sigma_R^2}[/latex] |
Standard deviation measures the variability of returns over a specific time period, such as daily, monthly, or quarterly. To make comparisons easier and more meaningful, standard deviation is often annualized, especially when analyzing the risk of investments.
To annualize standard deviation, the time period of the original data must be considered. The formula depends on the frequency of the original data (e.g., daily or monthly returns).
From Daily Standard Deviation to Annual Standard Deviation:
Assuming trading days in a year:
From Monthly Standard Deviation to Annual Standard Deviation:
Assuming months in a year:
From Quarterly Standard Deviation to Annual Standard Deviation:
Assuming quarters in a year:
Learning Objective 2: Diversification and the Risk and Return of a Portfolio
2.1 Diversification
- Definition
In reality, most investors do not hold just a single asset; instead, they build portfolios comprising multiple investments. Diversification is the practice of spreading investments across a variety of assets to reduce overall risk. A holding of various assets is referred to as a portfolio. The idea is that by combining assets with different risk and return characteristics, the negative performance of some investments can be offset by the positive performance of others, resulting in a more stable (i.e less volatile) portfolio.
For example, consider an investor who holds shares in both a technology company and a utility company. If the technology sector experiences a downturn, the utility company—often more stable and less affected by economic cycles—can help balance the losses. This reduces the overall portfolio risk compared to holding only technology stocks, demonstrating the power of diversification in managing investment risk.
- Principle of Diversification
The principle of diversification therefore lies in reducing the overall risk of a portfolio by spreading investments across a variety of assets, industries, or locations that do not move in perfect correlation. The idea is based on modern portfolio theory, which states that the total risk of a portfolio can be lowered without necessarily sacrificing expected returns, as long as the assets included have varying degrees of correlation.
When assets are combined in a portfolio, the asset-specific risks associated with individual investments tend to offset each other. This means that poor performance in one asset may be counterbalanced by strong performance in another, resulting in smoother, more stable overall returns.
Diversification works because different assets react differently to economic, market, or sector-specific events. For instance, stocks and bonds often have an inverse relationship—when stocks decline, bonds may hold steady or rise, thus balancing the portfolio's performance. The ultimate goal of diversification is to optimize the risk-return trade-off, ensuring that no single investment disproportionately affects the portfolio's overall performance.
When an investor holds a diversified portfolio, the relevant measure of risk and return is that of the portfolio as a whole, rather than the risk and return of individual assets within it. As a result, the portfolio's overall behaviour becomes the key factor in assessing risk and return. For the investor, it is the portfolio's total expected return and overall volatility (or standard deviation) that matter most, as these determine the portfolio's potential to achieve financial objectives.
- Diversifiable vs. Non-diversifiable risk
Diversification is an effective strategy to reduce risk as explained above. However, there is a limit to how much risk diversification can reduce. There are some types of risk that will always remain no matter how much an investor diversifies. The risk that can be reduced by combining assets in a portfolio is known as diversifiable (or non-systematic) risk while the risk that cannot be eliminated through diversification is known as non-diversifiable (or systematic) risk.
The difference between diversifiable and non-diversifiable risk lies in their scope and how they can be managed:
- Diversifiable Risk (Unsystematic Risk): This is risk specific to a particular company, industry, or asset. Examples include management decisions, product recalls, or competitive pressures. It can be reduced or eliminated through diversification by holding a well-balanced portfolio of different assets.
- Non-Diversifiable Risk (Systematic Risk): This is market-wide risk that affects all investments, such as economic recessions, interest rate changes, or political instability. It cannot be reduced through diversification because it impacts the entire market, and investors must accept it as inherent to investing.
The distinction between these two types of risk is very important to understand the risk-return trade-off that will be discussed later in this topic.
2.2 The return of a portfolio
The return of a portfolio is determined by two factors: the weight of each asset and the return on the assets. In other words, the return of a portfolio is the weighted average of the returns of the individual assets it comprises.
- Portfolio Weight
Portfolio weight refers to the proportion of the total investment allocated to a specific asset within a portfolio. It is calculated by dividing the value of the investment in a particular asset by the total value of the portfolio. Portfolio weights are important because they determine how much each asset influences the overall performance of the portfolio.
For example, if a portfolio is worth $100,000, with $40,000 invested in stocks, $30,000 in bonds, and $30,000 in real estate, the portfolio weights are 40% for stocks, 30% for bonds, and 30% for real estate. These weights influence how changes in each asset's value impact the total portfolio's return.
- Portfolio Return
As explained above, portfolio return is calculated as the weighted average of individual assets' returns.
In the context of portfolio return, a weighted average means calculating the overall return of the portfolio by taking into account the return of each individual asset and how much of the portfolio is invested in it. Each asset's return is multiplied by its "weight," which is the proportion of the total portfolio value invested in that asset. The results are then added together to get the total portfolio return.
| 2.7 | Expected return for a portfolio | [latex]E(R_p)=\sum_{j=1}^{n}{w_jE\left(R_j\right)}[/latex] |
For example, using the portfolio described above comprising of 40% stock, 30% bonds and 30% real estate, the portfolio return can be calculated as below assuming that the return on stocks is 8%, bonds is 5% and real estate is 7%.
The portfolio return is calculated by taking the weighted average of the returns of the individual assets in the portfolio. Here's a detailed breakdown for the given portfolio comprising stocks, bonds, and real estate:
- Stocks:
- Portfolio weight: 40% (or 0.4)
- Return: 8% (or 0.08)
- Contribution to portfolio return: or 3.2%
- Bonds:
- Portfolio weight: 30% (or 0.3)
- Return: 5% (or 0.05)
- Contribution to portfolio return: or 1.5%
- Real Estate:
- Portfolio weight: 30% (or 0.3)
- Return: 7% (or 0.07)
- Contribution to portfolio return: or 2.1%
Finally, the overall portfolio return is calculated by summing up the contributions from each asset:
E(R)=0.032+0.015+0.021=0.068 or 6.8%
This gives a portfolio return of 6.8%. Each asset's weight and return determine its influence on the overall return.
2.3 The Risk of a Portfolio
The risk, or standard deviation, of a portfolio returns depends on 3 factors:
- the individual risks of the assets it contains (standard deviation of individual assets)
- the proportion of each asset in the portfolio (weight of individual assets)
- the correlation of returns of individual assets, simply understood to be how returns of individual assets move together.
Having previously discussed the standard deviation as a measure of individual asset risk and the weights as the proportion of each asset in a portfolio, we now turn our attention to understanding how the returns of different assets move together. This relationship, known as correlation or covariance, is crucial in determining the overall risk of a portfolio. By analysing these interactions, we can assess how combining assets influences portfolio volatility and the benefits of diversification
- Covariance
Covariance is a statistical measure that indicates how two variables, such as the returns of two assets, move in relation to each other. If the covariance is positive, it means the returns of the assets tend to move in the same direction; if one increases, the other is likely to increase as well. Conversely, a negative covariance means the returns typically move in opposite directions.
- Correlation Coefficient
The correlation coefficient is another measure of how two variables, such as asset returns, move together. Unlike covariance, which provides an absolute measure, the correlation coefficient standardizes this relationship, expressing it as a value between -1 and 1. A value of 1 indicates perfect positive correlation, where the assets move in exactly the same direction, while -1 indicates perfect negative correlation, meaning the assets move in completely opposite directions. A value of 0 implies no correlation, signifying that the movements of the assets are unrelated.
Both covariance and correlation describe the relationship between variables, but while covariance measures the degree of co-movement in raw units, the correlation coefficient provides a scaled and more interpretable measure, making it easier to compare relationships across different assets.
- Benefits of Diversification
When assets in a portfolio have low or negative correlation, their returns move independently or in opposite directions, reducing the portfolio's overall volatility. This is because gains in one asset can offset losses in another, smoothing out fluctuations and lowering risk.
The benefit of diversification is maximized when assets are perfectly negatively correlated (correlation of -1), meaning their returns move exactly opposite to each other. In this scenario, it is theoretically possible to eliminate all portfolio risk. Conversely, the benefit of diversification is minimized when assets are perfectly positively correlated (correlation of +1), as their returns move in tandem, resulting in a portfolio that essentially mirrors the risk of the individual assets without any risk reduction. Thus, diversification is most effective when the portfolio includes assets with low or negative correlations.
- Measuring the Risk of a Portfolio
The calculation of the standard deviation of a portfolio becomes increasingly complex as the number of assets grows. This complexity arises because the standard deviation depends not only on the individual risks (standard deviations) of each asset but also on how all the assets interact with one another. Specifically, it requires accounting for all possible pairwise correlations in returns between the assets. For a portfolio with n assets, there are unique pairwise correlations to consider, in addition to the weights and standard deviations of each asset. As the number of assets increases, the number of pairwise relationships grows exponentially, making the computation of portfolio standard deviation more intricate and time-consuming.
Therefore, for the purpose of this unit, we will only illustrate the calculation of the variance and standard deviation for a 2-asset portfolio which is specified in Equation 2.8.
| 2.8 | Two-asset portfolio variance | [latex]\sigma \:_p^2=\:w_1^2\:\sigma \:_1^2+\:w_2^2\:\sigma \:_2^2+2w_1w_2\rho \:_{1,2}\:\sigma _1\sigma _2\:[/latex]
Or [latex]\sigma _p^2=\:w_1^2\:\sigma _1^2+\:w_2^2\:\sigma _2^2+2w_1w_2Cov\left(R_1,R_2\right)[/latex] |
Let's consider a simple example.
Suppose you invest in a portfolio that consists of two stocks. Stock Alpha is worth $50,000 and has a standard deviation of 20%. Stock Beta is worth $100,000 and has a standard deviation of 10%. The correlation between the two stocks is 0.85.
In this scenario, the weight of Alpha = 1/3 while the weight of Beta = 2/3. Using Equation 2.8, the variance of the portfolio can be calculated as:
Variance = (33.3%^2 x 20%^2) + (66.7%^2 x 10%^2) + (2 x 33.3% x 20% x 66.7% x 10% x 0.85) = 1.64%
The standard deviation is the square root of 1.64% which is 12.81%. The risk of the portfolio is therefore 12.81%.
2.4 What do the risk and return figures mean?
The return and standard deviation are key parameters used to understand portfolio risk and return, as they define the distribution of potential outcomes. The expected or mean return represents the average return the portfolio is likely to generate, providing a measure of potential reward. The standard deviation, on the other hand, measures the dispersion or variability of returns around the average. A higher standard deviation indicates that returns are more spread out, meaning the portfolio has a greater chance of experiencing returns that are significantly above or below the average. This increased variability translates to higher risk because it reflects greater uncertainty about the portfolio's actual performance. Together, these two parameters allow investors to assess the trade-off between potential rewards and the associated risks, helping them make informed decisions about their investment strategies.
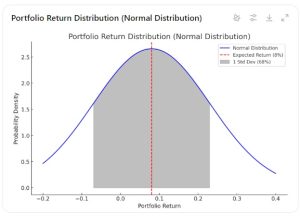
Assuming a portfolio with an expected return of 8% per annum and a standard deviation of 15%. What do these figures mean? These figures indicate that the possible returns on this portfolio follow a normal distribution where the expected return (i.e the most likely outcome) is 8% and 68% of the time the actual return falls within 1 standard deviation of the expected/mean return which is in the range of 8% - 15% = - 7% and 8% + 15% = 23%, represented by the shaded area in Figure 2.1 below.
Figure 2.1 Portfolio Return Distribution
As you can see, the higher the standard deviation (given the same expected return), the more the variability of return and hence the higher the risk of the portfolio.
Learning Objective 3: The Capital Asset Pricing Model (CAPM)
3.1 The risk return trade-off
The risk-return trade-off is a fundamental concept in Finance, highlighting the relationship between the level of risk and the potential reward of an investment. It states that higher returns typically require accepting greater risk, while lower-risk investments generally offer more modest returns. This trade-off reflects the need for investors to balance their willingness to take on risk with their return expectations, depending on their financial goals, time horizon, and risk tolerance. Understanding this relationship is essential for making informed investment decisions and building a portfolio that aligns with individual objectives.
However, not all risks are equal as some are rewarded with higher returns while others are not. Systematic risk, also known as market risk or non-diversifiable risk, is inherent to the entire market and cannot be eliminated through diversification. Examples include economic recessions, interest rate changes, or geopolitical events. Because systematic risk affects all investments, investors demand a higher return to compensate for bearing this unavoidable risk.
On the other hand, unsystematic risk, or diversifiable risk, is specific to individual assets, companies, or industries and can be mitigated by holding a diversified portfolio. Examples include company management decisions or industry-specific challenges. Since unsystematic risk can be reduced or eliminated through diversification, investors should not expect to be rewarded for taking on this type of risk. Consequently, efficient portfolio management focuses on minimizing diversifiable risk while accepting and managing systematic risk, which drives the expected return.
The premise that only systematic risk is rewarded for in the risk-return trade-off forms the foundation for the Capital Asset Pricing Model (CAPM) which provides a structured framework for the understanding of how the return on risky assets can be estimated. If an investor holds only one asset, a relevant measure of risk for the asset is its Total Risk which comprises of Systematic Risk and Unsystematic Risk. However, if an investor holds a diversified portfolio, the relevant measure of risk for the asset is only its Systematic Risk as Unsystematic Risk has been minimized through diversification.
3.2 The Capital Asset Pricing Model (CAPM)
CAPM is used to determine the expected return of an asset based on its risk relative to the overall market. It helps in pricing risky securities and evaluating whether an investment offers a favourable return given its risk.
There are a number of assumptions underlying the CAPM which include:
- Investors are rational and risk averse.
- Markets are efficient, meaning all available information is reflected in prices.
- Investors hold diversified portfolios to eliminate unsystematic risk (asset-specific risk).
- There are no taxes or transaction costs.
- All investors have the same expectations about returns and risks.
Under these assumptions, the expected return on a risky asset (i.e an asset where the return is uncertain) can be estimated as:
E(Ri)=Rf+βi(E(Rm)−Rf)
Let's examine Indvidual components of the CAPM.
- Risk-Free Rate (Rf): Represents the return on an investment with zero risk. A good proxy for the risk-free rate is the return on a government bond.
- Beta (β): Measures an asset's volatility relative to the market. A beta greater than 1 implies higher risk and higher potential return than the market, while a beta less than 1 implies lower risk and return.
- Market Risk Premium (E(Rm)−Rf): The difference between the market's expected return and the risk-free rate, reflecting the reward for taking on market risk.
3.3 Applications of the CAPM
The Capital Asset Pricing Model (CAPM) has numerous real-life applications, making it a valuable tool in finance and investing. Most important applications of CAPM are:
- Estimate the Cost of Equity
Financial managers use the Capital Asset Pricing Model (CAPM) to understand their company’s cost of equity, which represents the return investors expect for holding the company’s stock. CAPM provides a systematic way to calculate this expected return based on the stock’s sensitivity to market risk (beta), the return of the overall market, and the risk-free rate (such as government bond yields).
By using CAPM, financial managers can estimate how much return the company needs to generate to compensate shareholders for the risks they bear. This information is essential for setting the discount rate in investment appraisals, determining the company’s overall cost of capital, and making decisions about financing and growth strategies. CAPM simplifies the complex relationship between risk and return, offering managers a clear framework to evaluate equity costs and align financial planning with investor expectations.
- Security Selection
Investors used CAPM to determine if a security is overpriced or underpriced by comparing its expected return, as calculated using the CAPM formula, to its actual or forecasted return.
If the security’s actual return is greater than the expected return calculated using CAPM, it suggests the security is undervalued and offers a better return relative to its risk. Investors may see this as an opportunity to buy. Conversely, if the actual return is lower than the CAPM-calculated expected return, it indicates the security may be overpriced, as it provides a lower return for the level of risk taken. This comparison helps investors make informed decisions about whether to include a security in their portfolio, based on its alignment with their risk-return preferences.
Learning Objective 4: Financial Decision Making Under Uncertainty
Uncertainty in the real world arises from the inability to predict future events with complete accuracy due to dynamic and interconnected factors influencing financial markets and decisions. Unlike theoretical models, real-world decision-making is affected by imperfect information, evolving market conditions, and unforeseen events. For example, the COVID-19 pandemic created unprecedented uncertainty for global financial markets. Economies faced sudden lockdowns, disrupting supply chains, reducing consumer demand, and triggering market volatility. Companies had to make critical decisions, such as adjusting capital expenditures, managing liquidity, and navigating workforce disruptions, without a clear timeline for recovery or full understanding of the pandemic’s impact. This illustrates how real-world uncertainty challenges decision-makers to balance risk and flexibility while adapting to rapidly changing conditions.
4.1 Quantitative Tools
Quantitative tools help managers analyse complex situations, evaluate potential outcomes, and make informed decisions under uncertainty. Among these tools, scenario analysis, sensitivity analysis, Monte Carlo simulation, and decision trees are particularly valuable.
Scenario Analysis
Scenario analysis involves exploring different possible future scenarios to understand their impact on decisions. Managers construct "what-if" scenarios, such as best-case, worst-case, and most-likely outcomes, to evaluate the range of potential results. This technique is particularly useful for strategic planning, risk assessment, and evaluating investments.
Example: A company considering an international expansion might use scenario analysis to assess outcomes under three scenarios: rapid economic growth in the target market (best-case), moderate growth (most-likely), and a recession (worst-case). For each scenario, the company evaluates projected revenues, costs, and profitability to decide whether to proceed with the expansion and how to mitigate risks.
Sensitivity Analysis
Sensitivity analysis examines how changes in key variables influence outcomes. It identifies which factors have the greatest impact on decisions, allowing managers to focus on the most critical uncertainties.
Example: A project manager evaluating a new product launch might analyse how variations in production costs, sales volume, or pricing affect profitability. By identifying that sales volume is the most sensitive variable, the manager can prioritize efforts to improve market penetration and demand forecasting.
Monte Carlo Simulation
Monte Carlo simulation uses random sampling and statistical modelling to evaluate the probability of different outcomes. By running thousands of simulations, it provides a distribution of possible results, rather than a single deterministic output. This technique is ideal for complex decisions with multiple uncertain variables.
Example: A financial manager assessing the potential return of a portfolio might use Monte Carlo simulation to model market fluctuations, interest rates, and asset correlations. The simulation could generate a probability distribution showing the likelihood of different returns, helping the manager understand potential risks and rewards more comprehensively.
Decision Trees
Decision trees visually map out decisions, their possible outcomes, probabilities, and payoffs in a tree-like structure. This tool helps managers evaluate sequential decisions and choose the optimal path by weighing risks, rewards, and costs at each step.
Example: A pharmaceutical company deciding whether to develop a new drug might use a decision tree. The first decision node could represent the initial investment in R&D, followed by outcome nodes for successful or unsuccessful trials. The tree would also include probabilities for each outcome and the corresponding financial impact, allowing the company to determine whether the potential payoff justifies the risk.
4.2 Risk Aversion vs. Risk seeking
Risk aversion refers to the preference for outcomes with lower uncertainty, even if they offer lower potential returns. Risk-averse individuals or organizations prioritize stability and the avoidance of losses, often requiring additional compensation (higher expected returns) to accept greater risk. For instance, risk-averse investors may favour safer assets like bonds or blue-chip stocks over high-risk investments such as speculative stocks or cryptocurrencies. Firms with risk-averse management might choose projects with stable cash flows over high-risk, high-reward ventures, even if the latter could maximize shareholder value.
In contrast, risk-seeking behaviour reflects a preference for higher-risk options in pursuit of potentially greater rewards. Risk-seeking individuals or firms are willing to tolerate significant uncertainty, often betting on large potential payoffs. This behaviour can lead to bold decisions, such as investing heavily in speculative assets, pursuing innovative but unproven projects, or leveraging financial positions to amplify returns. A risk-seeking financial manager can destroy shareholder value by making overly aggressive decisions that expose the company to excessive risk without adequately considering the potential downsides. For example, risk-seeking managers may take on excessive debt to finance ambitious projects or acquisitions. While leveraging can amplify returns in favourable conditions, it increases financial vulnerability during downturns, leading to potential insolvency or forced asset sales.
4.3 Cognitive Biases
Cognitive biases are systematic errors in thinking that arise from the brain’s reliance on mental shortcuts, or heuristics, to simplify complex information processing. While these shortcuts can be helpful, they often lead to distorted perceptions, flawed judgments, and suboptimal decisions. In financial and managerial contexts, cognitive biases can significantly affect decision-making by influencing how risks, rewards, and probabilities are evaluated.
Some common cognitive biases that financial managers should be aware of include:
Overconfidence Bias:
- Decision-makers may overestimate their knowledge, skills, or ability to predict outcomes.
- This can lead to excessive risk-taking, such as over-trading in financial markets or committing to overly ambitious projects without adequate contingency planning.
- Imagine a CEO planning a large-scale acquisition based on their belief in the company’s ability to integrate and turn around struggling businesses. Despite limited experience in such transactions, the CEO dismisses concerns from the finance team and industry experts, believing their strategy will succeed. This overconfidence leads to the company overpaying for the acquisition, underestimating integration challenges, and ultimately incurring significant financial losses.
Loss Aversion:
- The tendency to prioritize avoiding losses over acquiring equivalent gains.
- To illustrate the loss aversion bias, consider the following scenario. A company has invested $10 million in a new product development project. Halfway through the project, market research reveals that demand for the product is much lower than anticipated, and competitors are releasing superior alternatives. The financial analysis suggests that continuing the project will likely result in additional losses, while abandoning it would save resources for other, more profitable ventures.
- Despite the clear evidence against the project's viability, the company’s executives decide to continue investing in it. Their decision is driven by loss aversion—the psychological discomfort of acknowledging the initial investment of $10 million as a loss. They hope that additional investment will "turn things around" and recoup the initial expenditure, even though the likelihood of success is low.
- This is clearly a poor decision as the company may end up spending another $5 million on a project that will be likely discontinued. The root cause of the problem is the financial manager avoids the recognition of loss and fails to make a rational choice based on facts.
Herding Behaviour:
- Following the actions of others without independent analysis, often leading to poor decisions.
- For example, a company operating in the technology sector notices that many of its competitors are heavily investing in artificial intelligence (AI) and machine learning technologies. Despite limited internal expertise or a clear strategic fit, the company’s leadership decides to allocate significant resources to AI development, driven by the fear of being left behind in a trend embraced by its peers. In this case, the company’s decision is based more on the actions of competitors than on a thorough evaluation of its own capabilities, market position, or potential return on investment.
- The company's rushed AI initiative is a poor decision as is it lacks the infrastructure and talent to implement the technology effectively. Meanwhile, resources that could have been used to strengthen its existing competitive advantages are diverted. The decision damages the company’s financial performance and weakens its strategic focus.
Summary: Key Concepts in this Topic
1. Risk and Return of a Single Asset
- Return: The gain or loss on an investment, typically expressed as a percentage. It is calculated using historical data or expected future cash flows.
- Risk: Measured by the variability of returns, commonly represented by the standard deviation. Higher variability indicates higher risk.
- Investors assess the trade-off between risk and return, aiming to maximize returns for a given level of risk or minimize risk for a desired return.
2. Risk and Return of a Portfolio
- Portfolio Return: Calculated as the weighted average of the returns of individual assets, where weights represent the proportion of each asset in the portfolio.
- Portfolio Risk: Determined by the variance and covariance of returns among assets. Diversification reduces unsystematic risk, but systematic risk remains.
- Diversification lowers overall portfolio risk by including assets with low or negative correlations, emphasizing the importance of asset allocation.
3. Capital Asset Pricing Model (CAPM)
- Purpose: CAPM is used to estimate the expected return of an asset based on its systematic risk, measured by beta.
- Formula:
Where:
- : Expected return of the asset.
- : Risk-free rate.
- : Asset’s sensitivity to market risk.
- : Market risk premium.
- Key Applications: Estimating the cost of equity, evaluating whether assets are overpriced or underpriced and optimizing portfolio decisions (security selection).
- CAPM links risk and return, emphasizing that only systematic risk is rewarded in the market.
4. Financial Decision-Making Under Uncertainty
- Challenges: Uncertainty arises from incomplete information, market volatility, and unforeseen events. Decisions must account for risks and their potential impacts.
- Tools and Techniques:
- Scenario Analysis: Evaluates outcomes under different future scenarios (e.g., best-case, worst-case).
- Sensitivity Analysis: Identifies how changes in key variables affect outcomes.
- Monte Carlo Simulation: Uses probabilistic modelling to assess potential results.
- Decision Trees: Visualize sequential decisions and their associated risks and payoffs.
- Cognitive Biases: Behavioural factors, such as overconfidence, loss aversion, and herding, can distort judgment, leading to suboptimal decisions.
- Effective decision-making requires balancing quantitative analysis, risk management, and awareness of cognitive biases.