仅仅确保项目在预算内按时完成项目是不够的。你需要做出正确的产品来满足利益相关者的需求。质量意味着要确保项目建造的是你说过的东西，而且要尽可能有效地完成。这意味着不要犯太多的错误，并始终保持你的项目朝着创造正确产品的目标努力。

每个人都 “知道 “什么是质量。但这个词在日常生活中的使用方式与它在项目管理中的使用方式有些不同。就像三重约束（范围、成本和进度）一样，你通过设定目标和进行测量来管理项目的质量。这就是为什么你必须了解你的利益相关者认为可以接受的质量水平，并确保你的项目达到这些目标，就像它需要满足他们的预算和进度目标一样。

客户满意度是指确保为最终产品付款的人对他们得到的东西感到满意。当团队为规范收集需求时，他们试图写下客户在产品中想要的所有东西，这样你就知道如何让他们满意。有些需求可以不被说明并且是由客户的需求所暗示的。有些要求只是常识性的（例如，人们持有的产品不能由可能杀死他们的有毒化学品制成）。这些要求可能没有被说明，但它肯定是必须的。

“适合使用 “是指确保你制造的产品有最好的设计来满足客户的需求。你会选择哪一个：一个设计精美、结构良好、坚固耐用、全方位令人愉快但却不能满足你需要的产品，还是一个尽管丑陋难用却能满足你需要的产品？你总是会选择适合你需求的产品，即使它有严重的局限性。这就是为什么产品既能做它应该做的事，又能做得很好，这一点很重要。例如，你可以用螺丝刀敲打钉子，但锤子更适合这项工作。

符合要求是客户满意度和适用性的核心，也是衡量产品在多大程度上完成了你的意图。最重要的是，产品需要做你在需求文件中写下的事情。你的要求应该考虑到什么能让客户满意，以及对工作的最佳设计。这意味着既要符合陈述的要求，也要符合隐含的要求。

最后，产品质量是否建造了你说要建造的东西来判断的。

质量规划的重点是在项目开始时利用所有可用的信息，并弄清楚将如何衡量质量和防止缺陷。你的公司应该有一个质量政策，说明它如何在整个组织内衡量质量﹑确保你的项目遵循公司的政策和任何政府的规则或条例。

你需要计划将使用哪些活动来衡量项目产品的质量。而且需要考虑所有你想做的与质量有关的活动的成本。然后，你需要为衡量的对象设定一些准则。最后，设计当产品准备好被测试时你要进行的测试。

质量和等级 Quality and Grade

根据国际标准化组织（International Standardization Organization，简称ISO）的说法，质量是 “反应实体满足主体明确和隐含需求的能力的特性总和”。一个产品或过程的要求可以被归类或给予一个等级，这将提供一个比较的基础。质量是由某物满足其等级要求的程度决定的。

对大多数人来说，质量这个词也意味着良好的价值——让你的钱花得值。例如，即使是低档次的产品也应该像预期的那样工作，使用起来很安全，并能持续合理的时间。

请考虑以下的例子：

统计数据 Statistics

确定产品在多大程度上符合等级要求是通过测量，然后对这些测量进行解释来完成的。统计学—对数字数据的数学解释— 在解释大量的测量结果时非常有用，当重复制造同一产品时，用于确定产品满足规格的程度。对产品样本的测量必须在控制范围内，即允许变化的上限和下限，管理部门要设计一个过程，使产品始终在这些限制之间。

教学设计者经常使用统计数据来确定其课程设计的质量。学生评估是教学设计者能够判断学习是否发生在控制范围内的一种方法。

如果一个过程被设计为生产某种尺寸或其他测量特性的产品，就不可能控制所有可能导致产品与所需测量值略有不同的小因素。其中一些因素会产生测量值大于期望值的产品，一些因素则会产生相反的效果。如果有几个随机因素在影响这个过程，它们往往会相互抵消，最常见的结果是在范围的中间附近；这种现象被称为中心极限定理。

如果把可能的测量值的范围平均分为被称为仓的分区，就可以对测量值进行分类，并计算出落入每个仓的测量值的数量。其结果是一个频率分布，显示有多少测量值落入每个仓。如果造成差异的影响是随机的，并且倾向于相互抵消，那么频率分布就被称为正态分布，它类似于一个边缘外扩的钟形形状。理论上正态分布曲线的边缘非常接近于零，但并没有达到零。

例子： 正态分布 （Normal Distribution）

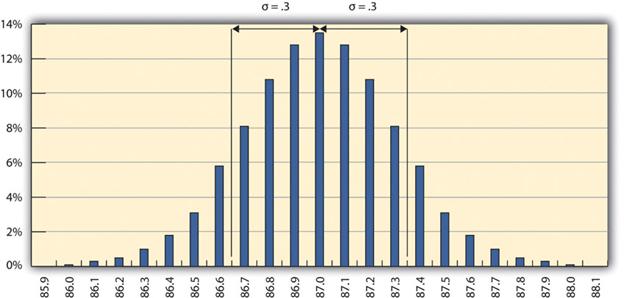
一个炼油厂的质量控制经理测量了许多辛烷值为87的汽油样品，将测量结果按辛烷值分类到0.1辛烷宽的仓中，然后计算每个仓中的测量数量。然后她创建了一个数据的频率分布图，如图14.1所示。

 

通常情况下，从总人口中随机选择子集，并测量和比较它们的质量，因为测量整个人口会很麻烦，甚至不可能。如果样本测量值像图14.1中那样在分布中心的上方和下方平均分布，那么这些测量值的平均值也是中心值，被称为平均值，在公式中用小写希腊字母μ（读作mu）表示。各个测量值与中心值的差异量被称为样本标准差或只是标准差。

 

计算标准差的第一步是将每个测量值从中心值（平均值）中减去，然后将该差值平方。(回顾一下你的数学课程，平方一个数字就是乘以它本身，结果总是正的。) 下一步是将这些平方的数值相加，然后除以数值的数量减去1。最后一步是去掉平方根。结果可以被认为是一个平均差。(如果你用通常的方法取平均值，那么正数和负数的总和将为零）。数学家用小写的希腊字母σ（读作sigma）表示标准差。如果测量的是一个群体的所有元素，而不仅仅是一个样本，那么它就被称为群体的标准差，在第二步中，将平方值的总和除以数值的总数。

 

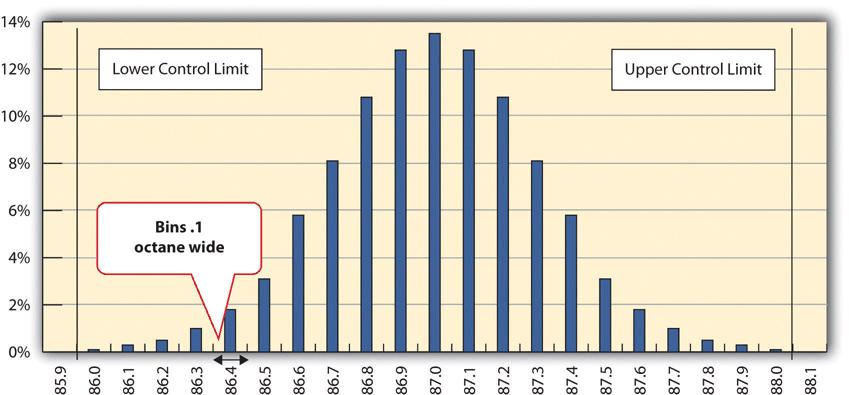
图14.1显示，最常见的辛烷值测量值接近87，其他测量值在87以上和87以下平均分布。分布图的形状支持中心极限定理的假设，即影响辛烷值的因素是随机的，并倾向于相互抵消，这一点从对称形状中可以看出。这种分布是正态分布的典型例子。质量控制经理注意到，没有一个测量值高于88或低于86，所以它们都在控制范围内，进而得出结论，这个过程的工作是令人满意的。

例子： 汽油样品的标准偏差

炼油厂的质量控制经理使用电子表格程序中的标准偏差功能来查找样品测量的标准偏差，发现对于她的数据，标准偏差是0.3辛烷值。她在频率分布图上标出了范围，以显示在平均值两侧的一个西格玛（标准偏差）内的数值（图14.2）。

 

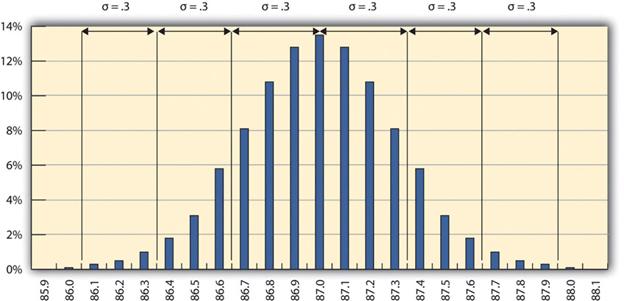
对于正态分布，大约有68.3%的测量值落在平均值两侧的一个标准差之内。这对于分析某些类型的数据来说是一个有用的经验法则。如果测量值之间的变化是由随机因素造成的，导致正态分布，有人告诉你平均值和标准差，你就知道有三分之二多一点的测量值在平均值两侧的一个标准差之内。由于曲线的形状，两个标准差内的测量值的数量是95.4%，三个标准差内的测量值的数量是99.7%。例如，如果有人说美国成年男子的平均身高是178厘米（70英寸），标准差约为8厘米（3英寸），你就会知道，美国68%的男子身高在170厘米（67英寸）和186厘米（73英寸）之间。你还会知道，美国大约95%的成年男子身高在162厘米（64英寸）和194厘米（76英寸）之间，几乎所有的人（99.7%）都在154厘米（61英寸）和202厘米（79英寸）之间。这些数字被称为68-95-99.7规则。

例子： 三个标准差内的汽油

如图14.3所示，炼油厂的质量控制经理对包括在两个和三个标准差内的范围进行标记。有些产品的变异性必须比其他产品小，以满足其目的。例如，如果对旨在操作高度专业化和有潜在危险的机器的培训进行质量评估，预计大多数参与者将超过可接受的合格率。对某些产品来说，与控制限值相差三个标准差可能没问题，但对其他产品来说就不行了。一般来说，如果平均值与两个控制限值相差6个标准差，那么一个零件因随机变化而超过控制限值的可能性几乎为零（十亿分之二）。

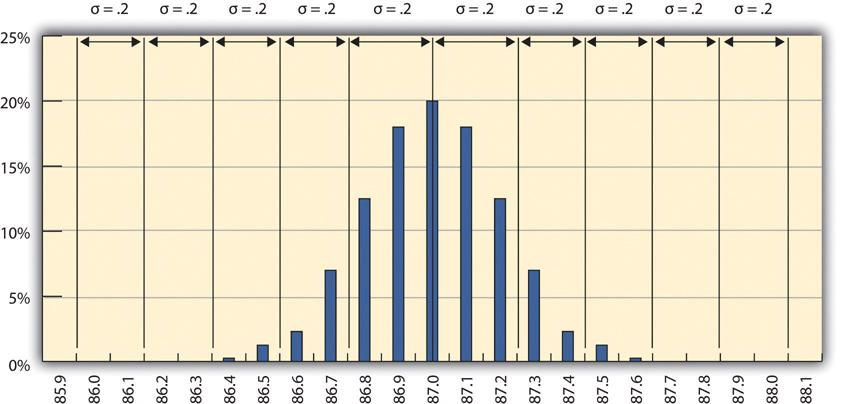
例子： 一个步骤项目改善了汽油的质量

因为炼油厂安装了一个新的步骤，生产的燃料变异性更小。炼油厂的质量控制经理采集了一组新的样品，并绘制了一个新的频率分布图，如图14.4所示。炼油厂的质量控制经理计算出，新的标准偏差是0.2辛烷值。由此，她可以使用68-95-99.7规则来估计，68.3%的生产燃料将在86.8和87.2之间，99.7%将在86.4和87.6辛烷值之间。描述这种控制量的速记方法是说这是一个五西格玛生产系统，指的是平均数和控制极限之间每边的五个标准偏差。

质量规划工具

高质量是通过规划来实现的，而不是在发现问题后做出反应，为实现相应标准选择标准并制定流程。

测量术语

在项目的执行阶段，对服务和产品进行抽样和测量，以确定质量是否在要求的控制范围内，并分析变化的原因。这种评估通常由一个单独的质量控制小组完成，了解一些过程测量术语对于理解他们的报告是必要的。这些术语中有几个是相似的，了解它们之间的区别是很有价值的。

质量计划规定了产品或过程的控制极限，这些极限之间的范围大小就是公差。公差通常被写成平均值，加上或减去公差。加号和减号写在一起，即±。

选择能够紧密测量样品的工具，以确定测量结果是否在控制限度内，以及是否显示出趋势。每个测量工具都有自己的公差。

公差的选择直接影响到质量成本（Cost of Quality, 简称COQ）。一般来说，生产和测量具有小公差的产品的成本更高。制作公差小的产品的相关成本可能非常高，与收益不成正比。例如，如果评估在线教程中每个屏幕的成本大于交付产品和事后修复任何问题的成本，那么COQ可能过高，教学设计者将容忍设计中的更多缺陷。

界定和满足客户的期望

客户为项目提供必须满足的规格，以使项目获得成功。回顾一下，满足项目规范是项目成功的一个定义。客户经常有一些期望，而这些期望在书面规范中是很难捕捉到的。例如，一个客户希望被邀请参加项目的每一次会议，然后选择那些看起来最相关的会议。另一个客户希望只被邀请参加需要客户意见的项目会议。邀请这位客户参加每一次会议将导致不必要的挫折。倾听客户的意见，了解那些不容易在规范中体现的期望，对满足这些期望很重要。

项目调查可以捕捉到客户对项目表现的看法，并为项目团队提供对满足客户期望有用的数据。如果调查的结果显示客户对项目的某些方面不满意，项目组就有机会与客户探讨这种看法的原因，并制定恢复计划。调查还可以帮助确定哪些方面进展顺利，哪些方面需要改进。

规划信息的来源

对质量的规划是初始规划过程的一部分。早期的范围、预算和进度估计被用来确定应该规定预期等级和质量的过程、服务或产品。风险分析用于确定项目的哪些风险可能影响质量。

技术

有几种不同的工具和技术可用于计划和控制项目的质量。这些工具的使用程度由项目的复杂性和客户使用的质量管理计划决定。

以下是项目经理可用的质量规划工具：

• 成本效益分析（Cost-benefit analysis）是看你的质量活动将花费多少钱，与你做这些活动将获得多少收益。成本很容易衡量；做这些活动所需的努力和资源，就像你计划中的其他任务一样。由于质量活动实际上并不生产产品，人们有时更难衡量收益。主要的好处是减少返工，提高生产力和效率，以及让团队和客户更满意。
• 标杆管理（Benchmarking）意味着使用其他项目的质量规划结果来为你自己的项目设定目标。你可能会发现，你公司的上一个项目比之前的项目少了20%的缺陷。你应该想从这样的项目中学习，并把他们用来做出如此巨大改进的任何想法付诸实践。基准可以在你开始工作之前给你一些判断自己项目的参考点。
• 实验设计（Design of experiments）是你要对你的产品进行的所有种类的测试的清单。它可能会列出你要做的所有种类的测试程序，你要采取的方法，甚至测试本身。(在软件领域，这被称为测试计划）。
• 质量成本（Cost of quality）是指当你把你在项目中要做的所有预防和检查活动的成本加起来时得到的东西。它不只是包括测试。它包括任何花在编写标准、审查文件、开会分析缺陷的根本原因、在团队发现缺陷后进行返工修复的时间：换句话说，绝对是你为确保项目质量所做的一切。质量成本可以是一个很好的检查数字，以确定你的项目是做得好还是有问题。假设你的公司跟踪其所有项目的质量成本；那么你就可以知道，为了使你的项目达到质量标准，你的花费是比其他项目的花费多还是少。
• 控制图（Control charts）可以用来定义可接受的限度。如果一个项目的某些功能是重复性的，可以用统计过程控制来确定趋势，并将过程控制在控制限度内。控制重复过程质量的计划的一部分是确定控制限度是什么以及如何对过程进行抽样。
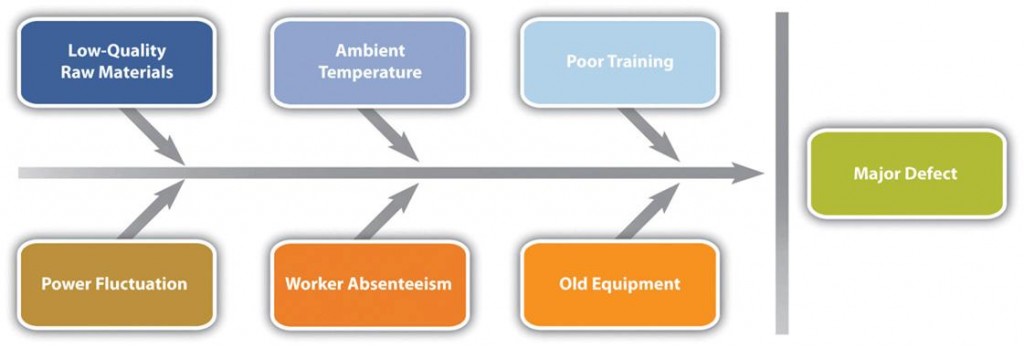
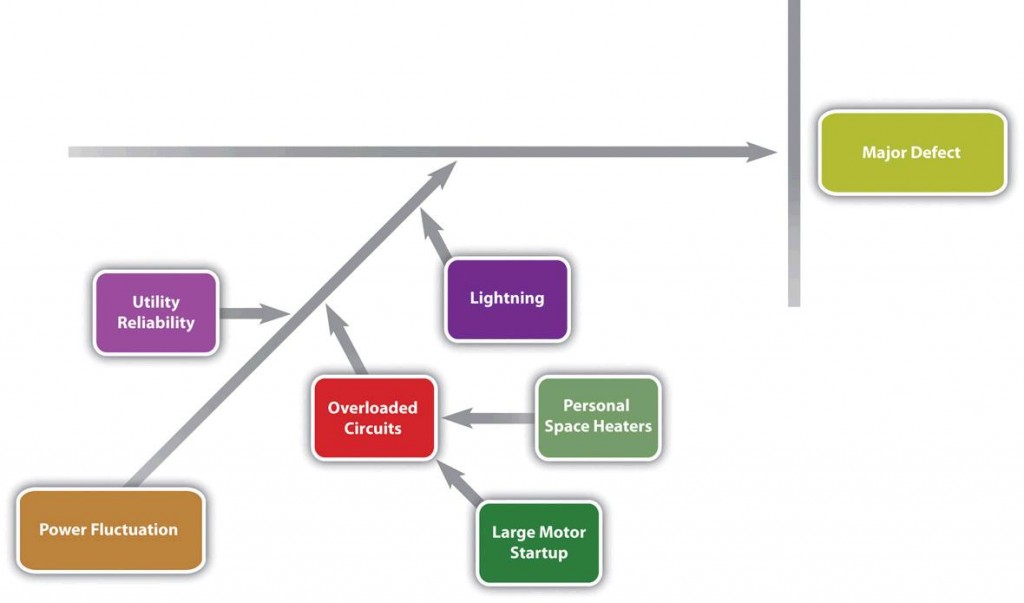
• 因果关系图（Cause-and-effect diagrams）可以帮助发现问题。当控制图显示一个可分配的变异原因时，要确定问题的原因并不容易。可以用因果图或鱼骨图来促进旨在发现原因的讨论，鼓励参与者找出缺陷的可能原因。

例子 ：绘制质量问题的图表

一家小型制造企业试图找出其生产线上的变化的可分配的原因。他们组建了一个团队，确定了六种可能性：

• 低质量的原材料
• 电源波动
• 环境温度
• 工人缺勤
• 培训不足
• 设备陈旧

这些可能性中的每一种都被组织成图14.5中的鱼骨图：

 

图中的每个分支都可以扩展，将一个类别分解成更具体的项目。 一位工程师和一位电工在其中一个分支上工作，考虑电力波动的可能原因：

• 公用事业的可靠性
• 个人空间加热器和大型电机的启动导致电路过载
• 照明

这些项目被添加到鱼骨图的各自部分，如图14.6所示。

检查表、直方图（histograms）和帕累托图（Pareto charts）被用来解决几个质量问题。当一个质量控制问题发生时，项目经理必须选择首先解决哪个问题。确定质量问题优先级的一个方法是确定哪些问题出现的频率最高。这些数据可以用检查表来收集，检查表是一个基本的表格，用户可以在每次发生问题时在适当的框中打勾，或者用适当的技术使数据收集过程自动化。一旦收集了数据，就可以通过创建一种叫做直方图的频率分布图来进行分析。真正的直方图是一种柱状图，柱子的宽度填满了X轴上的可用空间，并与该轴上显示的类别值成正比，而柱子的高度则与出现的频率成正比。大多数直方图使用一种宽度的列来代表一个类别，而纵轴代表出现的频率。

直方图的一个变种是经济学家维尔弗雷多·帕累托发明的频率分布图，称为帕累托图，其中列按递减顺序排列，最常见的列在左边，并加上一条线，显示累积总数。列和线的组合使用户能够一目了然地知道哪些问题是最常见的，它们占总数的多少。

一旦你有了你的质量计划，你就知道你管理项目质量的准则。你监控项目质量的策略应该包括在计划中，以及你所采取的所有步骤的原因。重要的是，团队中的每个人都要理解用于判断项目成功或失败的指标背后的理由。

质量保证

质量保证的目的是建立信心，相信质量计划和控制是正常工作的。必须分配时间来审查最初的质量计划，并将该计划与项目实施过程中的质量保证方式进行比较。

流程分析 Process Analysis

将质量过程的流程图与实际操作过程中遵循的流程进行比较。如果计划没有得到遵守，则对该过程进行分析并采取纠正措施。纠正措施可以是教育有关人员如何遵循质量计划，也可以是修改计划。

对抽查产品和过程并收集数据的实验进行检查，看他们是否遵循统计学上有效的抽样技术，以及测量方法是否有足够小的公差来检测控制限度内的变化。

由于项目是临时性的，在一个项目中学习和改进的机会较少，特别是如果项目持续时间较短的话。但是，即使在短期项目中，质量经理也应该有办法从经验中学习，并为下一个类似复杂情况的项目改变流程。

质量保证的目的是使客户对质量标准和程序得到遵守建立信心。这是通过对计划、测试和修订政策的内部审查或者由外部团体或机构对相同项目进行审计来实现的。

贡献者和归因 Text Attributions

This chapter of 企業策略: 高管項目領導指南 Strategy Consulting: A guide for executives leading projects is a derivative of the following text:

• This chapter was adapted and remixed by Adrienne Watt from the following sources:
  • Introductory text and text under “Quality Planning tools” in Project Management for Skills for All Careers by Project Management Open Resources and TAP-a-PM. Licensed under a CC BY 3.0 licence.
  • Text under “Quality and Grade”, “Statistics” and “Quality Assurance” is from “Assuring Quality” in Project Management for Instructional Designers by Amado, M., Ashton, K., Ashton, S., Bostwick, J., Clements, G., Drysdale, J., Francis, J., Harrison, B., Nan, V., Nisse, A., Randall, D., Rino, J., Robinson, J., Snyder, A., Wiley, D., & Anonymous.  Licensed under a CC BY-NC-SA (Attribution-NonCommercial-ShareAlike) licence.

  Media Attributions

  • Normal Distribution of Measurements © Wiley et al is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
  • One Sigma Range © Wylie, et al. is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
  • 68-95-99 Rule © Wiley et al is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
  • Smaller Standard Deviation © Wiley et al is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
  • Cause and Effect Diagram © Wiley et al is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
  • Power Fluctuation Diagram © Wiley et al is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license