13 Two Sample Tests for Means

Learning Outcomes

At the end of this chapter you should be able to:

  1. identify the difference between a paired samples and independent samples test;
  2. conduct a hypothesis test for paired samples;
  3. conduct a hypothesis test for two independent samples;
  4. compute the pooled variance for two independent samples;
  5. verify assumptions for the models used in the hypothesis tests;
  6. compute confidence intervals for a single mean and a difference of means.

 

Contents

13.1 Paired samples t-test test

13.2 Independent samples t-test

13.3 Summary

 

13.1 Paired Samples t-test

Consider an experiment in which there is one treatment and one control group. Differences between the profile of subjects in each group can cause problems.

Example 13.1 A small clinical trial

Four patients with a rare disease are recruited to a clinical trial.
The patient’s characteristics are as follows.

Patient Age  Sex
A 71 M
B 68 M
C 28 F
D 34 F

Two patients are to be assigned to the treatment group, and two to the control group. If we did this completely at random, we could get patients A and B in the treatment group, and C and D in the control group. This could cause problems.

  1. Suppose that the disease tends to be worse in men than women. Then the outcomes for the treatment and control group may be very similar even though the treatment is beneficial, since the benefits are counterbalanced by the increased acuteness of the disease in men.
  2. The same argument could also be made in terms of age rather than sex.
  3. Suppose that the treatment group do have better outcomes than the control group. It will be impossible to say whether this is due to the treatment, or due to the fact that the disease tends to be worse in women (or in the young).

We can use a Matched Pairs design to adjust for these differences. The idea is to select experimental units in pairs that are `matched’ on potentially important characteristics, such as subject age and sex in a clinical trial. We then randomly assign one member of each pair to the treatment group, and the other member of the pair to the control group. The result is a treatment group and a control group that are very similar in terms of important characteristics of the experimental units (i.e. the variability between subjects is controlled).

In the clinical trial example, patients A and B form a matched pair, as do patients C and D. We should randomly assign A and B to different groups, and C and D to different groups.

It is often possible to `match’ an individual to him/herself, and look at results under two different experimental conditions (e.g. before and after some treatment).

Example 13.2

Twenty students studying European languages took a two week intensive course in spoken German. To assess the effectiveness of the course, each student took a spoken German test before the course, and an equivalent test after the course. The before and after test scores on each student are  paired observations.

The model

We have two populations with means \mu_1, \mu_2. A sample from each population is selected, where the samples have a natural pairing. Often each pair of observations is on the same unit, as in “before” and “after” experiments.

The hypotheses of interest are:

    \[H_0:\mu_1-\mu_2 = 0\]

against one of the alternatives,

    \[H_1: \mu_1-\mu_2 \ne 0, {\rm \ or\ } H_1: \mu_1-\mu_2 > 0, {\rm \ or\ } H_1: \mu_1-\mu_2 < 0\]

depending upon the question of interest.

Let X_1,X_2,\dots,X_n and Y_1,Y_2,\dots,Y_n be the samples from the two populations with means \mu_1 and \mu_2 respectively, with pairs (X_i,Y_i), \; i=1,2,\dots,n. Let D_i = X_i - Y_i be their difference, i=1,2,\ldots,n, and let \mu_D be the mean and S_D be the standard deviation of this difference. Then the standardised sample mean

    \[T = \frac{\overline D - \mu_D}{S_D/\sqrt{n}} \sim t_{n-1},\]

where

  • the distribution is exact if the 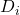D_i are normally distributed;
  • the distribution is approximate if the 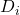D_i are not normally distributed AND the sample size is large (n \ge 30).

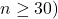The hypothesis test is now based on the differences. The hypothesis of interest in terms of \mu_1 and \mu_2 is expressed in terms of \mu_D, as below.

    \[H_0: \mu_1-\mu_2 = 0 \Rightarrow H_0: \mu_D = 0\]

against one of the alternative hypotheses:

    \[H_1: \mu_1-\mu_2 \ne 0 \Rightarrow H_1: \mu_D \ne 0\]

    \[H_1: \mu_1-\mu_2 > 0 \Rightarrow H_1: \mu_D > 0\]

    \[H_1: \mu_1-\mu_2 < 0 \Rightarrow H_0: \mu_D < 0\]

Note that the order of subtraction is important as it determines the alternative hypothesis.

Differencing has reduced the data set to just one sample, so the test now proceeds exactly as the one-sample t-test.

Example 13.3

The presence of trace metals in drinking water not only affects the flavor but an unusually high concentration can pose a health hazard. Measurements of zinc concentrations (in parts per billion (ppb))were taken at ten locations in bottom water and surface water. Does the data suggest that the true average concentration in the bottom water exceeds that of surface water?

Location (i) 1 2 3 4 5 6 7 8 9 10
Zinc Concentration

in bottom water (x_i)

 0.430 0.266 0.567 0.531 0.707 0.716 0.651 0.589 0.469 0.723
Zinc Concentration in

surface water (y_i)

 0.415 0.238 0.390 0.410 0.605 0.609 0.632 0.523 0.411 0.612
Difference

(d_i = x_i-y_i)

 0.015 0.028 0.177 0.121 0.102 0.107 0.019 0.066 0.058 0.111

    \[\overline d = 0.0804, s_d = 0.05227.\]

Solution

The hypotheses of interest are

    \[H_0: \mu_D = 0 \quad H_1: \mu_D > 0,\]

where \mu_D is the mean difference in the zinc concentrations between the bottom water and surface water.
The test statistic is

    \[T = \frac{\overline D - \mu_D}{S_D/\sqrt{10}} \sim t_{9}.\]

Since the sample size is small we need to assume that the differences are normally distributed.

    \begin{align*} t_{obs} &= \frac{0.0804- 0}{0.05227/\sqrt{10}} = 4.864\\ {\rm p-value} &= P(T > 4.864) = 0.0004 < 0.025, \end{align*}

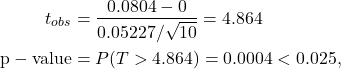
1-pt(4.864,9)
[1] 0.0004454422

so there is conclusive evidence against the null hypothesis. We conclude that the mean zinc concentration in the bottom water is greater than that in the surface water.

A 95% confidence interval for the mean difference in zinc concentrations is (using the t_9^{0.025} = 2.262 value)

    \[\left(0.0804 - 2.262 \times \frac{0.05227}{\sqrt{10}}, 0.0804 - 2.262 \times \frac{0.05227}{\sqrt{10}}\right) = \left(0.0430,0.1178\right) {\m ppb}.\]

Note that this interval does not contain 0, consistent with our hypothesis test that the mean difference in concentrations is positive.

Example 13.4

A bank wants to know if omitting the annual credit card fee for customers would increase the amount charged on its credit cards. The bank makes this no-fee offer to a random sample of 250 of its customers who use its credit cards. It then compares how much these customers charged this year with the amount they charged last year. The mean increase is $350 and the standard deviation of the change is $1200.

(a) Is there significant evidence at the 1% level that the mean amount charged has increased under the no-fee offer? State the appropriate hypotheses and carry out a hypothesis test, clearly stating your conclusion. State any assumptions required for the analysis to be valid.

(b) What are the consequences for the bank of a Type I error here?

(c) Compute a 95% confidence interval for the mean increase in the amount charged.

Solution

Let the random variable D denote the increase in amount charged. Then we assume D \sim N(\mu, \sigma^2), where \mu is the mean increase. From the data,

    \[\overline d = 350, s_d = 1200, n = 250.\]

(a) The hypotheses of interest are

    \[H_0: \mu = 0 \quad H_1: \mu > 0\]

The test statistic is

    \[T = \frac{\overline D - \mu}{s/\sqrt{250}} \sim t_{249}.\]

The observed value of the test statistic is

    \[t_{obs} = \frac{350-0}{1200/\sqrt{250}} = 4.6117.\]

The p-value is

    \[p-value = P(T > 4.6117) = 3.20 \times 10^{-6} < 0.025,\]

so there is overwhelming evidence against the null hypothesis. We conclude that the omitting the credit card fee has increased the mean amount charged.

(b) A Type I Error would occur if the null hypothesis is rejected when it is true. In this case the bank would incorrectly conclude that the mean amount charged has increased under the no fee initiative when it has not. This may cost the bank in the fee without any benefit.

(c) 95% CI is

    \[\left(350 - 1.9695 \times \frac{1200}{\sqrt{250}}, 350 + 1.9695 \times \frac{1200}{\sqrt{250}}\right) = \left(\$200.52, \$499.48)\]

where 1.9695 is the 2.5% critical value of the t_{249} distribution.

13.2 Independent samples t-test

Now the two samples are independent, and there is no natural pairing. Also, often the samples are of different sizes. An example is: investigating the difference in salary between male and female executives.

Population 1: mean = \mu_1, variance = \sigma_1^2

Sample 1: sample size = n_1, mean = \overline X_1, variance = S^2_1

Population 2: mean = \mu_2, variance = \sigma_2^2
Sample 2: sample size = n_2, mean = \overline X_2 variance = S^2_2

The model

The model equation is

    \[y_{ij} = \mu_i + \epsilon_{ij},\]

where y_{ij} is observation j from population i=1,2, j = 1,2,\ldots,n_i.

So, i=1 denotes population 1, and the model equation becomes

    \[y_{1j} = \mu_1 + \epsilon_{1j}\]

y_{1j} denote the observations from the first sample, and y_{2j} denote the observations from the second sample.
Assume that the two samples are from normal populations.

Hypotheses

The hypotheses are

    \[H_0:\mu_1 - \mu_2 = 0\]

versus one of

    \begin{align*} H_1:& \mu_1 - \mu_2 \ne 0\\ H_1:& \mu_1 - \mu_2 > 0\\ H_1:& \mu_1 - \mu_2 < 0 \end{align*}

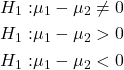
NOTE:

The order of subtraction is important and depends on the question of interest.

Model assumptions

The model has the following assumptions.

  1. The individual samples are from normally distributed populations.
  2. The variance of the two populations are equal (or homogeneous). This is also referred to as homoscedacity.
  3. Each sample is independent and the two samples are independent of each other.

We will discuss later how to verify these assumptions.

Pooled variance

Note that the sample means may be different. We have assumed \sigma_1^2=\sigma_2^2=\sigma^2, that is, the two populations have a common variance. In practice \sigma_1^2 and \sigma_2^2 are unknown and need to be estimated. We estimate this common variance by the  pooled variance. Since the two sample means may be different, but the variances are (assumed) equal, we compute the sum of squares about each mean separately, and then weight these by the sample sizes. The pooled variance is given by

    \[S^2_p = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2}}\]

Test statistic

Using our results from sampling, the standardised difference in sample means is

    \[Z = \frac{(\overline X_1-\overline X_2) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim {\rm N}(0,1)\]

where the distribution is exact if the populations are normal, and only approximate if the populations are not normal AND each sample size is at least 30.

Since we are assuming the population variances are equal, we replace the variances by \sigma^2, so this gives

    \[Z = \frac{(\overline X_1-\overline X_2) - (\mu_1-\mu_2)}{\sigma\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim \N(0,1)\]

Finally, we approximate this common variance \sigma^2 by the pooled sample variance S^2, and this gives

    \[T = \frac{(\overline X_1-\overline X_2) - (\mu_1-\mu_2)}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t_{n_1+n_2-2}\]

NOTE:

The order of subtraction is important, and depends on the hypotheses.

Example 13.5

In a medical study, 12 men with high blood pressure were given calcium supplements, and 16 men with high blood pressure were given placebo. The reduction in blood pressure (in mm Hg) over a ten week period was measured for both groups. The summary statistics for the first (i.e. treatment) group were

    \[n_1= 12, \quad \overline x_1 = 4.10,\quad s_1 = 6.42\]

and for the second (i.e. control group) were

    \[n_2 = 16, \quad \overline x_2= 0.03 \quad s_2 = 5.25\]

Is the reduction in blood pressure greater for the group who received calcium supplements?

Solution

Let \mu_1 and \mu_2 denote the mean decrease in blood pressure for the treatment (calcium) and control (placebo) groups respectively. The hypotheses of interest are:

    \[H_0:\mu_1 - \mu_2 = 0 \qquad H_1:\mu_1 - \mu_2 > 0\]

First we estimate the pooled variance.

    \begin{align*} s^2_p &= \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}\\ &= \frac{11\times 6.42^2 + 15 \times 5.25^2}{12+16-2} = 33.34. \end{align*}

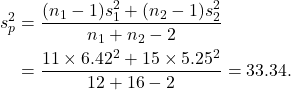
The observed value of the test statistic is then

    \[t_{obs} = \frac{(\overline x_1-\overline x_2) - (\mu_1-\mu_2)}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} = \frac{4.10-0.03}{\sqrt{33.34}\sqrt{\frac{1}{16}+\frac{1}{12}}}= 1.846.\]

The p-value of the test is P(T > 1.846) = 0.0382 > 0.025, so there is insufficient evidence to reject the null hypothesis. We concluded that there is no significant difference in mean blood pressure reduction for the two groups.

Conclusion: Calcium supplements do not reduce blood pressure significantly.

Equal Variance assumption

The equal variance assumption can be verified by using one of Bartlett’s or Levene’s tests, available in R. Note that these tests require the original data.

Another informal way to verify this assumption is that the ratio of the larger variance to the smaller should not be greater than 2. In the last example,

    \[\frac{s_1^2}{s_2^2} = \frac{6.42}{5.25} = 1.22 < 2\]

so there is no reason to doubt the equal variance assumption.

Confidence Interval for a Difference on Population Means

The general form of a confidence interval for a parameter \theta is

    \[100(1-\alpha)\% {\rm \ CL\ for\ } \theta = \hat \theta \pm t_{df}^{\alpha/2} \times SE(\hat \theta),\]

where

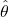  1. \hat \theta is a point estimate of \theta;
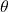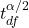  2. t_{df}^{\alpha/2} is the 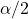\alpha/2 level critical value. (Note that the distribution from which this critical
    value can be different, depending on what is being estimated. We will always need just the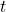 t or normal distributions.)
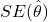  3. SE(\hat \theta) is the standard error of the point estimate \hat \theta.

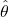The confidence interval is a simple matter of unravelling the test statistic,

    \[T = \frac{(\overline X_1-\overline X_2) - (\mu_1-\mu_2)}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\]

If we write the expression for (\mu_1-\mu_2) from this we get

    \[100(1-\alpha)\% {\rm \ CL\ for\ } (\mu_1-\mu_2) = (\overline X_1-\overline X_2) \pm t_{df}^{\alpha/2} \times S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}},\]

where the df = n_1+n_2-2, the denominator for the estimate of the variance.

Note

  1. We used the 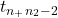t_{n_+n_2-2} distribution in this case, because the denominator for the estimate of variance here was
    n_1+n_2-2
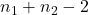
  2. This same t-distribution will be used whenever a t-distribution is needed in this context.

Example 13.5 (ctd)

The df for the t-distribution is n_1+n_2-2=12+16-2=26. The corresponding 2.5% critical value for the t_{26} distribution is 2.056. Then a 95% CI for \mu_1-\mu_2 is given by

    \begin{align*} (\overline x_1 - \overline x_2) \pm t_{26}^{0.025} \times S\sqrt{\frac{1}{12}+\frac{1}{16}} &= (4.10-0.03) \pm 2.056 \times \sqrt{33.34}\sqrt{\frac{1}{12}+\frac{1}{16}}\\ &= 4.07 \pm 4.534\\ &= (-0.4635,8.604) {\rm mm\ Hg}. \end{align*}

Note

  1. This interval includes 0. Thus at the 5% level of significance we will not reject

        \[H_0: \mu_1-\mu_2=0\]

    in favour of 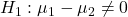H_1: \mu_1-\mu_2 \neq 0 and at the 2.5% level of significance we will not reject

        \[H_0: \mu_1-\mu_2=0\]

    in favour of

        \[H_1: \mu_1-\mu_2 > 0\]

    (or the left-sided test).

  2. If the interval not does include 0, then at the 5% level of significance we will reject

        \[H_0: \mu_1-\mu_2=0\]

    against

        \[H_1: \mu_1-\mu_2 \neq 0.\]

  3. This establishes the relationship between hypothesis tests and confidence intervals.

Confidence Interval for a Single Mean

A confidence interval for a single mean is given by:

    \[100(1-\alpha)\% {\rm \ CL\ for\ } \mu_1 = \overline X_1 \pm t_{df}^{\alpha/2} \times S\sqrt{\frac{1}{n_1}}.\]

Note: Be careful!

  1. Note that this has a similar form to the CI for a single sample mean.
  2. However, the pooled standard deviation is used, as it is a better estimate of population standard deviation.
  3. Consequently, the corresponding df for the t-distribution is 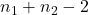n_1+n_2-2. So the same critical value is used.
  4. But, the denominator is 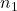n_1, the sample size corresponding to \overline X_1.

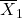Example 13.5 (ctd)

The df for the t-distribution is n_1+n_2-2=12+16-2=26. The corresponding 2.5% critical value for the t_{26} distribution is 2.056. Then a 95% CI for \mu_1 is given by

    \begin{align*} \overline x_1 \pm t_{26}^{0.025} \times S\sqrt{\frac{1}{12}} &= 4.10 \pm 2.056 \times \sqrt{33.34}\sqrt{\frac{1}{12}}\\ &= 4.10 \pm 4.534\\ &= (0.673,7.527) {\rm mm\ Hg}. \end{align*}

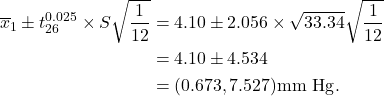
Exercise

Compute a 95% confidence interval for \mu_2 for this example. You will find that there is significant overlap between the confidence intervals for \mu_1 and \mu_2. This provides evidence that the two means are not different at the 5% level of significance.

Example 13.6

Severe idiopathic respiratory distress syndrome (SIRDS) is a serious condition that can affect newborn infants, often resulting in death. The table below gives the birth weights (in kilograms) for two samples of SIRDS infants. The first sample contains the weights of 12 SIRDS infants that survived, while the second sample contains the weights of 14 infants that died of the condition.

Survived 1.130 1.680 1.930 2.090 2.700 3.160 3.640 1.410 1.720 2.200 2.550 3.005
Died 1.050 1.230 1.500 1.720 1.770 2.500 1.100 1.225 1.295 1.550 1.890 2.200 2.440 2.730

It is of interest to medical researchers to know whether birth weight influences a child’s chance of surviving with SIRDS. Define population 1 to be the population of SIRDS infants that survive, with mean \mu_1 and variance \sigma_1^2. Let population 2 be the population of non-surviving SIRDS infants, with mean \mu_2 and variance \sigma_2^2.

We will address the following questions.

(a) Is there significant evidence that the population mean birth weights differ for survivors and non-survivors?

(b) Compute a 95% confidence interval for the difference between the population means.

Solution

(a) We shall test

    \[H_0: \mu_1 - \mu_2 = 0 {\rm \ against\ }H_1: \mu_1 - \mu_2 \ne 0\]

We now need to decide whether or not to assume equal population variances. The sample standard deviations are 0.758 for group 1 (survived) and 0.554 for group 2 (died). The ratio of larger to smaller is 0.758/0.554 = 1.37 < 1.5, suggesting the an assumption of common variance is not too unreasonable.

We shall conduct the test in R. The commands and output are below.

survived <- c(1.130,1.680,1.930,2.090,2.700,3.160,3.640,1.410,1.720,2.200,2.550,3.005)
died <- c(1.050,1.230,1.500,1.720,1.770,2.500,1.100,1.225,1.295,1.550,1.890,2.200,2.440,2.730)

(ttest <- t.test(survived, died, var.equal = TRUE))

	Two Sample t-test

data:  survived and died
t = 2.0929, df = 24, p-value = 0.04711
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.007461898 1.071228578
sample estimates:
mean of x mean of y 
 2.267917  1.728571

The observed value of the t-statistic is t=2.09, which gives a p-value of 0.04711. We have sufficient evidence to reject H_0 at a 0.05 significance level. Note that the evidence is marginal.

(b) A 95% confidence interval for \mu_1 - \mu_2 is

    \[(0.00746, 1.07129).\]

Note that this confidence lies above 0. This indicates that \mu_1 \ne \mu_2, that is the mean weight of surviving children is different from those who did not survive. From the data, the mean weight of surviving children is higher.

Summary

  1. Paired t-test: Difference the data and perform a one-sample t-test on the differences.
  2. Independent samples t-test

    \begin{align*} S^2_p &= \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2}\\ T &= \frac{(\overline X_1-\overline X_2) - (\mu_1-\mu_2)}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\\ 100(1-\alpha)\% {\rm \ CL\ for\ } (\mu_1-\mu_2) &= (\overline X_1-\overline X_2) \pm t_{df}^{\alpha/2} \times S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\\ 100(1-\alpha)\% {\rm \ CL\ for\ } \mu_1 &= \overline X_1 \pm t_{df}^{\alpha/2} \times S\sqrt{\frac{1}{n_1}} \end{align*}

Licence

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Statistics: Meaning from data Copyright © 2024 by Dr Nazim Khan is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book