16 Multiple Linear Regression
Learning Outcomes
At the end of this chapter you should be able to:
- understand the concept of multiple linear regression;
- analyse given data in R using linear regression;
- interpret the results of regression analysis;
- explain the use of categorical variables in regression;
- perform model diagnostics;
- determine any appropriate transformation of data;
- evaluate models.
Contents
16.2 Model Fitting and Selection
16.3 Model Diagnostics — Residual Analysis
16.5 Building the Regression Model
16.6 Including Categorical variables in the model
16.1 Introduction
In the last chapter we analysed the Beetle data in detail. This was an example of simple linear regression. We now consider multiple linear regression, which includes more than one explanatory variable.
Example 16.1 Price of lamb
The following data is on the price of whole live lamb. The data is available in the file lamb.txt in the Appendix.
| Variable | Explanation |
|---|---|
| Year | Year |
| Price | Price of whole live lamb |
| Consumption | Per capita consumption of lamb |
| FoodIndex | Retail food price index (%) |
| Income | Disposal income per capita |
| FoodConsumption | Food consumption index per capita |
| IncomeIndex | Index of real disposable income per capita |
| CPIAdj | Retail food price index CPI adjustment |
The summary of the data is given below.
> lamb<-read.table("lamb.txt", header=T) > summary(lamb)
Year Price Consumption
Min. :2005 Min. :56.00 Min. :46.00
1st Qu.:2009 1st Qu.:63.40 1st Qu.:49.00
Median :2013 Median :70.20 Median :53.70
Mean :2013 Mean :69.06 Mean :53.09
3rd Qu.:2017 3rd Qu.:73.00 3rd Qu.:55.20
Max. :2021 Max. :82.20 Max. :60.00
FoodIndex Income FoodConsumption
Min. :4.160 Min. :29.40 Min. :8.730
1st Qu.:4.780 1st Qu.:40.80 1st Qu.:9.000
Median :5.140 Median :44.50 Median :9.070
Mean :5.422 Mean :44.62 Mean :9.101
3rd Qu.:6.480 3rd Qu.:52.10 3rd Qu.:9.110
Max. :6.800 Max. :56.30 Max. :9.750
IncomeIndex CPIAdj
Min. :5.320 Min. :7.330
1st Qu.:6.400 1st Qu.:7.980
Median :6.960 Median :8.450
Mean :6.865 Mean :8.332
3rd Qu.:7.250 3rd Qu.:8.770
Max. :8.950 Max. :8.990
The model equation for the full model (that is, including all the variables) is
![]()
Fitting the model in R gives the following output.
lamb.lm<-lm(Price ~ Consumption + FoodIndex + Income + FoodConsumption + IncomeIndex + CPIAdj, data=lamb) > summary(lamb.lm) Call: lm(formula = Price ~ Consumption + FoodIndex + Income + FoodConsumption + IncomeIndex + CPIAdj, data = lamb) Residuals: Min 1Q Median 3Q Max -2.2913 -0.7621 0.1914 1.1036 2.0770 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 213.363 57.335 3.721 0.00397 ** Consumption -1.096 0.148 -7.409 2.29e-05 *** FoodIndex 23.620 15.870 1.488 0.16751 Income -3.975 2.006 -1.981 0.07573 . FoodConsumption -15.996 6.027 -2.654 0.02415 * IncomeIndex 26.203 12.723 2.059 0.06646 . CPIAdj -8.535 10.355 -0.824 0.42903 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.672 on 10 degrees of freedom Multiple R-squared: 0.9635, Adjusted R-squared: 0.9416 F-statistic: 43.99 on 6 and 10 DF, p-value: 1.28e-06
In the output, the table of coefficients gives p-values for individual coefficients, so we can test for significance of each variable separately.
- Intercept
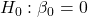 against
against 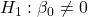 p-value
p-value 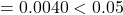 Reject
Reject 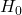
- Consumption:
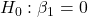 against
against 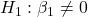 p-value
p-value 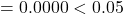 Reject
Reject 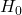
- FoodIndex:
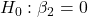 against
against 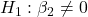 p-value
p-value 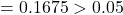 Fail to reject
Fail to reject 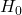
- Income:
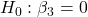 against
against 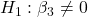 p-value
p-value 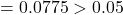 Fail to reject
Fail to reject 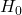
- FoodConsumption:
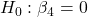 against
against 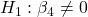 p-value
p-value 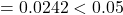 Reject
Reject 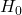
- IncomeIndex:
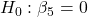 against
against 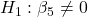 p-value
p-value 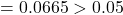 Fail to reject
Fail to reject 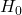
- CPIAdj:
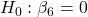 against
against 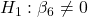 p-value
p-value 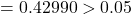 Fail to reject
Fail to reject 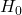
Only two variables are significant so far. Model Equation based on the significant variables is
![]()
16.2 Model Fitting and Selection
How do we know if we have the best model? That is, how do we know which variables to include in the model? The model should include only significant variables. Thus to find the best model we remove non-significant variables from the model one at a time, re-fitting the model at each stage, until the variables that remain are all significant.
Not so simple!
Multiple regression can be very tricky! Sometimes removing/including one variable can make another variable significant, which was not previously significant! Sometimes removing/including one variable can make another variable, which was previously significant, non-significant!
General Advice: Some experimentation is required with multiple regression! Often adding and removing variables to see their effect can give some insight into the data and the best model.
Significant terms in the Lamb model
The p-values indicate which variables are significant in the model. Thus FoodIndex, Income, IncomeIndex and CPIAdj are not significant at the 5% level. The model should be refitted to include only significant variables. The procedure is to omit the non-significant variable with the largest p-value and refit the model. The coefficients will change and significances of variables may also change. Some variables that were non-significant may now become significant.
So we refit the model by omitting the variable CPIAdj. The output is given below.
> lamb.lm1<-update(lamb.lm,.~.-CPIAdj)
##The update command is used to update an existing model.
> summary(lamb.lm1)
Call:
lm(formula = Price ~ Consumption + FoodIndex + Income + FoodConsumption +
IncomeIndex, data = lamb)
Residuals:
Min 1Q Median 3Q Max
-2.2961 -0.9603 -0.0510 1.0334 2.1738
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 194.1883 51.6330 3.761 0.003150 **
Consumption -1.0995 0.1458 -7.543 1.14e-05 ***
FoodIndex 10.9979 4.1046 2.679 0.021431 *
Income -2.4255 0.6916 -3.507 0.004908 **
FoodConsumption -14.1197 5.4990 -2.568 0.026157 *
IncomeIndex 16.0729 3.2453 4.953 0.000434 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.647 on 11 degrees of freedom
Multiple R-squared: 0.961, Adjusted R-squared: 0.9433
F-statistic: 54.23 on 5 and 11 DF, p-value: 2.228e-07
Now all the remaining variables are significant! The multiple R is almost unchanged (from 0.9635 to 0.961) from the full model (with all the variables in it). However, the Adjusted R Squared has increased (from 0.9416 to 0.9433)!
Note that R Squared does not adjust for the number of variables in the model. However, if another variable is added to the model it will (almost always) not decrease the R Squared. A simpler model, that is, one with fewer variables, is to be preferred over one with more variables.
Adjusted R squared
Recall that the adjusted R Squared adjusts for the number of variables in the model. Now
![]()
and
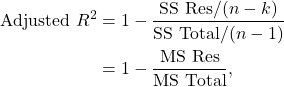
where ![]() number of observations and
number of observations and ![]() number of variables. The Anova table for the lamb data model is given below.
number of variables. The Anova table for the lamb data model is given below.
> anova(lamb.lm1)
Analysis of Variance Table
Response: Price
Df Sum Sq Mean Sq F value Pr(>F)
Consumption 1 433.49 433.49 159.736 6.815e-08 ***
FoodIndex 1 73.50 73.50 27.082 0.0002926 ***
Income 1 78.04 78.04 28.756 0.0002294 ***
FoodConsumption 1 84.23 84.23 31.036 0.0001674 ***
IncomeIndex 1 66.57 66.57 24.529 0.0004338 ***
Residuals 11 29.85 2.71
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The total sum of squares is (note the syntax used here)
(SST <- sum(anova(lamb.lm1)[2]))
[1] 765.661
with degrees of freedom
(Totdf <- sum(anova(lamb.lm1)[1]))
[1] 16
The residual sum of squares is
(SSRes <- anova(lamb.lm1)[2][[1]][6])
[1] 29.8515
with degrees of freedom
(Resdf <- (anova(lamb.lm1)[1][[1]][6]))
[1] 11
Then the R-squared is
(Rsq <- 1-SSRes/SST)
[1] 0.961012
The adjusted R-squared is
![]()
(AdjRsq <- 1- (SSRes/Resdf)/(SST/Totdf))
[1] 0.94329
Better model
A better model will have a (significantly) larger Multiple R or R squared and Adjusted R Squared, and a smaller residual standard error.
16.3 Model diagnostics–Residual analysis
All diagnostics and model checking are as for ANOVA in Chapter 15.
Normal probability plot
Plot shows only slight departure from straight line, so normality assumption does not seem to be violated. (Sample size is too small to judge anyway!)
Histogram of Residuals
The histogram does not seem too different from that expected from a normal distribution, given the sample size. On the basis of the normal probability plot and the histogram of residuals, we conclude that the normality assumption is not violated.
Standardised Residuals against Predicted Values
The plot shows no clear pattern and no outliers (none of the points are beyond 2 or ![]() ). We conclude that a linear model is appropriate. Also, no change in spread with predicted values is observed, so we conclude there is no evidence against the homogeneous variance assumption.
). We conclude that a linear model is appropriate. Also, no change in spread with predicted values is observed, so we conclude there is no evidence against the homogeneous variance assumption.
16.4 Variable transformation
Often the relationship between the response and explanatory variables is not linear. In this case the data needs to be transformed. Scatter plots will give some guidance on the sorts of models to try.
Graphs of some common functions
We will use these functions in model building examples.
16.5 Model building
Example 16.2 Case Study: La Quinta Profitability
Kimes and Fitzsimmons (1990) looked at the profitability of La Quinta Inns, using linear regression model based on location variables. La Quinta Motor Inns is a moderately priced hotel chain oriented towards serving the business traveller, and the aim was to determine which site locations are profitable. Location is one of the most important decisions for the hotel industry. Data was collected over 3 years on 57 established inns belonging to La Quinta. The regression model of Kimes and Fitzsimmons is
![]()
where
State population = state population (in thousands) per inn,
Tarrif = room rate for the inn,
ColStudents = number of college students (in thousands) within 6.5 km,
MedIncome = median income of the area.
The equation predicts that profitability will increase when Tarrif and number of college students increases, and when state population and median income decrease.
Reference: Kimes, S. E., & Fitzsimmons, J. A. (1990). Selecting Profitable Hotel Sites at La Quinta Motor Inns. Interfaces, 20(2), 12–20. http://www.jstor.org/stable/25061327. Accessed 24 Sept. 2023.
The first step to model building is data exploration. In particular, examine scatter plots of the response variable with each explanatory variable. This will give some indication of the form of the relationship — linear or non-linear. For non-linear relationships, transform the variable accordingly. The proceed with fitting a model with all the variables and remove the least significant term. Repeat this until the model contains only significant terms.
Residual analysis
Once a model has been fitted, the residuals contain information on the missing elements of the model. Plot of residuals against fitted values and other variables will reveal what other terms are needed in the model. We illustrate the procedure by the following example.
Example 16.3
Consider the following scatter plot of data containing two variables only.
The relationship is clearly non-linear. But what model do we fit?
Model building
First fit a simple linear model. Then examine a plot of residuals against fitted values and against ![]() . This will reveal what other terms should be included in the model.
. This will reveal what other terms should be included in the model.
The model equation is
![]()
The plot of residuals against fitted values is given below.
The plot shows a quadratic trend, so we include a quadratic term in the model. The model equation is
![]()
The plot of residuals against fitted values for this model is given below.
> #############Model 2 > m2.lm <- lm(y ~ I(x^2) + x) > summary(m2.lm) Call: lm(formula = y ~ I(x^2) + x)#Note the notation I(x^2) to fit the square term. Residuals: Min 1Q Median 3Q Max -0.45914 -0.07501 -0.00184 0.09164 0.16288 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.141e+01 6.114e-02 186.7 <2e-16 *** I(x^2) 2.475e-01 1.627e-04 1521.6 <2e-16 *** x 2.748e+00 6.878e-03 399.6 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.1225 on 37 degrees of freedom Multiple R-squared: 1, Adjusted R-squared: 1 F-statistic: 3.07e+07 on 2 and 37 DF, p-value: < 2.2e-16 > oldpar <- par(mfrow = c(1,2)) > plot(m2.lm$residuals ~ m2.lm$fitted.values, xlab = "Fitted Values", ylab = "Residuals", main = "Model 2: Quadratic") > plot(m2.lm$residuals[1:20] ~ m2.lm$fitted.values[1:20], xlab = "Fitted Values", ylab = "Residuals", main = "Model 2: Quadratic") > par(oldpar)
Note that the residuals are much smaller than for Model 1. The pattern is less clear, but the second plot over a smaller portion indicates similarity with a square root function. So next we include a square root term as well. The model equation is
![]()
> #############Model 3 > m3.lm <- lm(y ~ I(x^2) + x + I(sqrt(x))) > summary(m3.lm) Call: lm(formula = y ~ I(x^2) + x + I(sqrt(x))) Residuals: Min 1Q Median 3Q Max -1.283e-13 -1.345e-14 -1.592e-15 1.547e-14 1.295e-13 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.000e+01 7.447e-14 1.343e+14 <2e-16 *** I(x^2) 2.500e-01 1.347e-16 1.855e+15 <2e-16 *** x 2.500e+00 1.284e-14 1.947e+14 <2e-16 *** I(sqrt(x)) 1.200e+00 6.116e-14 1.962e+13 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.798e-14 on 36 degrees of freedom Multiple R-squared: 1, Adjusted R-squared: 1 F-statistic: 2.129e+32 on 3 and 36 DF, p-value: < 2.2e-16 > oldpar <- par(mfrow = c(1,2)) > plot(m3.lm$residuals ~ m3.lm$fitted.values, xlab = "Fitted Values", ylab = "Residuals", main = "Model 3") > plot(m3.lm$fitted.values ~ y, xlab = "Observed values", ylab = "Fitted values", main = "Model 3") > par(oldpar)
First note that the residuals are almost zero, and indicate no pattern. There is nothing more to add to the model. Indeed the model equation that has been arrived is exact, and is the one used to obtain the data. The plot of fitted values against the observed values shows a perfect fit.
This example illustrated the power of residual analysis to obtain a model from data. This is very useful especially in situations where no other guidance is available.
Model diagnostics
The normal probability plots show that the residuals are not different from normal. The plot of residuals against fitted values (seen earlier) shows no pattern, so model assumptions are satisfied.
16.6 Including categorical variables
Often the explanatory variables are not continuous but categorical.
Example 16.4
We want to investigate the effect of Age and Sex on the monthly income. We define
![Rendered by QuickLaTeX.com \[{\rm Male} = \begin{cases} 1, & \text{if person is Male}\\ 0, & \text{otherwise.} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-3cefb501cd655e78e6d357450d90844a_l3.png)
The model equation is
![]()
When Male is 1, the equation is
![]()
When Male is 0, the equation is
![]()
Note that ![]() is the difference between the Male and Female incomes on average. If
is the difference between the Male and Female incomes on average. If ![]() is significantly different from
is significantly different from ![]() then the incomes for Males and Females are different. In particular, if
then the incomes for Males and Females are different. In particular, if ![]() then Male employees are paid more then Female employees. The output of the model for some hypothetical data is given below. Wage is in $10,000 and Age is in tens.
then Male employees are paid more then Female employees. The output of the model for some hypothetical data is given below. Wage is in $10,000 and Age is in tens.
Income.lm<-lm(MonthlyIncome~Age.10years+Male,data=Income) > summary(Income.lm) Call: lm(formula = MonthlyIncome ~ Age.10years + Male, data = Income) Residuals: Min 1Q Median 3Q Max -0.136697 -0.067380 0.001351 0.054888 0.154863 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.73206 0.23558 3.107 0.00906 ** Age.10years 0.11122 0.07208 1.543 0.14880 Male 0.45868 0.05346 8.580 1.82e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.09679 on 12 degrees of freedom Multiple R-squared: 0.89, Adjusted R-squared: 0.8717 F-statistic: 48.54 on 2 and 12 DF, p-value: 1.773e-06
In this case we defined Male as 1 for male workers and 0 for female workers. However, R is able to admit categorical variables directly into a model. In the following output, Sex takes the values Female and Male, that is, Sex is a factor.
Income.lm1<-lm(MonthlyIncome~Age.10years+Sex,data=Income) > summary(Income.lm1) Call: lm(formula = MonthlyIncome ~ Age.10years + Sex, data = Income) Residuals: Min 1Q Median 3Q Max -0.136697 -0.067380 0.001351 0.054888 0.154863 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.73206 0.23558 3.107 0.00906 ** Age.10years 0.11122 0.07208 1.543 0.14880 Sexmale 0.45868 0.05346 8.580 1.82e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.09679 on 12 degrees of freedom Multiple R-squared: 0.89, Adjusted R-squared: 0.8717 F-statistic: 48.54 on 2 and 12 DF, p-value: 1.773e-06
Note that in the output we see the variable Sexmale. R by default uses the first level in alphabetical order as a reference, and then estimates the coefficients for the other levels in the categorical variable. For both outputs the model equation is the same. Both outputs show that for the same Age, male workers are paid $4586.80 more on average.
16.7 Problems with linear regression
Multi-collinearity: a situation where two or more of the explanatory variables are highly correlated (linearly related). This causes several problems, particularly in parameter estimation, significance testing and interpretation of results.
Solution: Of the variables that are correlated, include only the most important variable in the model.
However:
- If the model is mainly for predicting/forecasting, then multicollinearity is not a problem.
- If the model is for understanding and explaining the behaviour of the response variable using the explanatory variable, then of the variables that are correlated, include only the most important variable in the model.
Outliers and points of high leverage
As in simple linear regression, outliers and points of high leverage are still a problem. The same approach as for simple linear regression is taken here. That is, fit the model with and without these points and compare results.
16.8 Data transformation
The linear regression model requires the residuals to be normal. Examination of a histogram of the residuals will indicate if this assumption holds. If the residuals are skewed, then sometimes this can often be corrected by transforming the response variable.
Which transformation?
We covered this is Chapter 2.9. With right skewed data, try square root or cube root. If neither works then try log–this is the most severe transformation for right skewed data. The idea is that these transformation pull together larger value more than the smaller ones, that is, they pull the right tail in. For example, for data 1, 4, 9, 6, 25, the square root gives 1, 2, 3, 4, 5, which are much closer to each other,
With left skewed data, try square or cube. If neither works then try exponential–this is the most severe transformation for left skewed data. The idea is that these transformation pull the right tail out.
Example 16.5
Data on the number of units of power produced (Units) and the cost of production (Cost) is plotted below. Determine how the Cost depends on the number of Units produced. The data is available in the file Power.txt.
Power <- read.table("Power.txt", header = T, sep = "\t)
with(Power, plot(Cost ~ Units))
Solution
The plot shows some curvature, so a linear model does not seem appropriate. However, we will start with the linear model.
power.lm<-lm(Cost~Units, data=Power) summary(power.lm) Call: lm(formula = Cost ~ Units, data = Power) Residuals: Min 1Q Median 3Q Max -4180.2 -1657.8 583.4 1701.7 2847.1 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 23226.921 651.804 35.63 <2e-16 *** Units 34.977 1.048 33.36 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1969 on 98 degrees of freedom Multiple R-squared: 0.9191, Adjusted R-squared: 0.9182 F-statistic: 1113 on 1 and 98 DF, p-value: < 2.2e-16
plot(Power$Cost~Power$Units,xlab="Units",ylab="Cost",main="Linear Model") abline(power.lm) power.res<-rstandard(power.lm) plot(power.res~power.lm$fitted.values,ylab="Standardised residuals", xlab="Fitted values",main="Linear Model")
The model equation is
![]()
The linear model shows systematic misfit, with all the points alternating from below the line of fit, then above and then below. The plot of residuals against fitted values indicates a clear quadratic trend. We next include a quadratic term in the model.
power.lm1<-update(power.lm,.~.+I(Units^2)) summary(power.lm1) Call: lm(formula = Cost ~ Units + I(Units^2), data = Power) Residuals: Min 1Q Median 3Q Max -1658.18 -324.82 14.82 416.52 1381.32 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.174e+03 6.418e+02 8.062 1.98e-12 *** Units 1.030e+02 2.316e+00 44.501 < 2e-16 *** I(Units^2) -5.767e-02 1.942e-03 -29.703 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 622.9 on 97 degrees of freedom Multiple R-squared: 0.992, Adjusted R-squared: 0.9918 F-statistic: 6001 on 2 and 97 DF, p-value: < 2.2e-16
The model equation is
![]()
The quadratic model fits much better, and especially captures the curvature at the high end. It has a lower standard error and a higher adjusted R square. The residual plots also shows no pattern and no evidence against the homogeneous variance assumption.
We next investigate a log model for the data.
power.lm2<-lm(Cost~I(log(Units)),data=Power) summary(power.lm2) Call: lm(formula = Cost ~ I(log(Units)), data = Power) Residuals: Min 1Q Median 3Q Max -2589.59 -742.87 97.55 866.66 1843.81 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -80238.3 1917.8 -41.84 <2e-16 *** I(log(Units)) 19624.2 302.6 64.85 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1044 on 98 degrees of freedom Multiple R-squared: 0.9772, Adjusted R-squared: 0.977 F-statistic: 4206 on 1 and 98 DF, p-value: < 2.2e-16
> x <- seq(min(Power$Units), max(Power$Units), 10) > fitpower2 <- power.lm2$coefficients[1] + power.lm2$coefficients[2]*log(x) > plot(Power$Cost~Power$Units,xlab="Units",ylab="Cost",main="Log model") > lines(x, fitpower2) > text(600, 40000, expression(Cost = -80238.3 + 19624.2*log(Units))) > plot(power.lm2$residuals ~ power.lm2$fitted.values, xlab = "Fitted values", ylab = "Residuals", main = "Log model") > qqnorm(power.lm2$residuals, main = "Normal Q-Q Plot: Log model") > qqline(power.lm2$residuals) > hist(power.lm2$residuals, xlab = "Residuals", main = "Log Model") > box() > par(oldpar)
The model equation is
![]()
The model fits well. The residual plot is better than linear, and comparable to quadratic model. The histogram of residuals shows slight left skewness.
Is the log model better than the quadratic model?
Comparing quadratic and log model
| Model | Standard Error | Adjusted R Square |
|---|---|---|
| Linear | 1969 | 0.9182 |
| Quadratic Model | 622.9 | 0.9918 |
| Log Model | 1044 | 0.977 |
Based on the measures in the table above, the quadratic model is the best. However, the problem with the quadratic model is interpretation. According to this model, as units increase, the negative coefficient of ![]() means that the parabola bends downward. This means that cost decreases as units increase. This is not reasonable.
means that the parabola bends downward. This means that cost decreases as units increase. This is not reasonable.
The log model is more appropriate, and indicates that as the number of units produced increases the cost flattens off. This is consistent with intuition and reality. So although the quadratic model is a better regression model, the logarithmic model is more realistic in this context.
16.9 Summary
- Multiple regression is a very powerful tool, that allows a range of models to be fitted.
- Some exploration and experimentation is required to identify the best model.
- Transformation of data may be required to satisfy model assumptions and to find a better model.
- A better regression model does not mean a better business model. Some intuition and reasoning is required to find the better business model.

