One Sample Hypothesis Tests

Dr R. Nazim Khan

12 One Sample Hypothesis Tests

Learning Outcomes

At the end of this chapter you should be able to:

understand the concept of hypothesis testing;
conduct a test of hypothesis for a population mean;
explain the concept of a p-value;
explain the difference between a one-sided and two-sided test;
explain the types of errors in hypothesis tests;
conduct a hypothesis test for a population proportion;
understand the relationship between a hypothesis test and a confidence interval.

12.1 Introduction

Statistical inference is the process of obtaining information about populations based on sampling. By this process we are concluding that what we see in the sample can be generalised to the population from which the sample was obtained. We use probability models to describe the random processes involved in producing the data, and inference then involves obtaining information about model parameters. This takes two forms:

Estimation simply aims to evaluate the values of any parameters given the data.
Hypothesis testing. The aim here is to evaluate evidence for benchmark (pre-held, prior) values of parameters, based on the data.

In this section we discuss hypothesis testing for population mean $\mu$ and population proportion $p$ . The methods for these are similar. We will develop the method with an example.

12.2 Hypothesis Tests for Population Mean

Problem A manufacturer claims that the mean weight of a brand of detergent is at least 3.25kg. A random sample of 64 boxes gave a sample mean weight of 3.238kg and a sample standard deviation of 0.117kg. What do we conclude about the manufacturer’s claim?

This is a typical hypothesis testing problem. The parameter of interest here is the population mean weight $\mu$ .

The model equation here is

$y_i = \mu + \epsilon_i$

for $i=1,2,\ldots,n$ . In this case the mean is a constant.

Method

STEP 1: State the null and alternative hypotheses.

The NULL HYPOTHESIS, $H_0$ , states the current, accepted belief about the parameter.

NULL = NO CHANGE.

The ALTERNATIVE HYPOTHESIS, $H_1$ , states the expected change.

The hypotheses come from the question. In this question:

$H_0: \mu \ge 3.25 \quad H_1: \mu < 3.25.$

So the null hypothesis believes the claim to start off with, and the alternative hypothesis states the counter claim.

STEP 2: Select a test statistic and find its distribution.

The test is for the population mean, so we use the standardised sample mean, and the sample standard deviation.

Test statistic:

$T = \frac{\overline X - \mu}{S/\sqrt{n}} \sim t_{n-1},$

where $n = 64$ .

STEP 3: Compute observed value of test statistic from data, ASSUMING $H_0$ IS TRUE.

$\overline x = 2.238, s = 0.117, n = 64$ , so

$t_{obs} = \frac{3.238 - 3.25}{0.117/\sqrt{64}} = -0.82,$

where we have use the value $\mu = 3.25$ from the equality value in the null hypothesis.

STEP 4: Find the p-value of the test statistic.
This is the probability the test statistic takes values at least as extreme as that observed, assuming $H_0$ is true.

$p-value = P(T \le -0.82) = 0.2007,$

where $T \sim t_{63}$ . Note that the direction of the inequality in the probability statement is the same as that in the alternative hypothesis. The R code for obtaining this probability is given below, where the second argument is the degrees of freedom.

pt(-0.82, 63)
[1] 0.2076539

STEP 5: Decision Rule.

Rationale

If $H_0$ is true then $\bar{x}$ should be close to the hypothesised value of $\mu$ . Then $T$ should be close to 0, and the p-value will be large. If $H_0$ is false then $T$ will be far from 0, and the p-value will be small.

Thus the p-value assesses the evidence in favour of $H_0$ provided by the data.

p-value small $\qquad \Rightarrow$ data inconsistent with $H_0$ .

$\qquad\qquad\qquad\qquad$ Evidence to reject $H_0$ .

p-value large $\quad \Rightarrow$ no reason to doubt $H_0$ .
$\quad\quad\quad\quad$ Data consistent with $H_0$ .
$\quad\quad\quad\quad$ Fail to reject $H_0$ .

What do we mean by “small”? We specify a significance level, $\alpha$ .

If the p-value $< \alpha$ reject $H_0$ at the significance level.
If the p-value $> \alpha$ fail to reject $H_0$ at the significance level.

We usually take $\alpha=0.025$ for a one-sided test (that is, the alternative hypothesis is a stated as $\theta > \theta_0$ or $\theta < \theta_0$ .

In our example, $p-value = 0.2077 > 0.025$ , so there is insufficient evidence to reject the null hypothesis at the 2.5% level of significance.

STEP 6: Conclusion. MUST BE STATED IN TERMS OF THE QUESTION.

We conclude based on the data that there is no evidence to doubt the manufacture’s claim.

Notes

In Step 2, the distribution of the test statistic comes from the discussion in Chapter 10.
We could take the hypotheses as

$H_0: \mu = 3.25 \quad H_1: \mu < 3.25$

[BUT NOT $H_0: \mu > 3.25 \quad H_1: \mu \le 3.25$ .]

The equality value ALWAYS appears in the null hypothesis. In computing the observed value of the test statistic the boundary value (that is, the equality value) in the null hypothesis is used.

3. The p-value is the probability of extreme values with respect to the null hypothesis. The direction of the tail (lower or upper) follows the direction of the inequality in $H_1$ .

Example 12.1

A manufacturer of light bulbs claims that bulbs it produces last more than 1000 hours on average. A random sample of 100 bulbs are tested by a consumer affairs officer, and the sample mean and standard deviation of the lifetimes are 991.0 hours and 87.2 hours respectively. What should the manufacturer conclude regarding the mean lifetimes of the bulbs?

Solution

Let $\mu$ denote the mean lifetime of the lightbulbs. The hypotheses of interest are:

$H_0: \mu = 1000 \quad H_1: \mu < 1000.$

Note that this is a lower tail test. The test statistic is

$T = \frac{\overline X - \mu}{S/\sqrt{100}} \overset{\cdot}{\underset{\cdot}{\sim}} t_{99},$

by the CLT, since $n = 100 \ge 30$ . The observed value of the test statistic is

$t_{obs} = \frac{991.0 - 1000}{87.2/\sqrt{100}} = -1.03.$

Take the significance level $\alpha = 0.025$ . The p-value is

$p-value = P(T < -1.03) = 0.1535 > 0.025,$

so there is insufficient evidence to reject the null hypothesis at the 2.5% level of significance.

Conclusion Based on this analysis, there is no evidence against the manufacture’s claim. We conclude the mean lifetime of the bulbs is more than 1000 hours.

12.3 Type I and Type II Errors

The hypothesis test is based on a single sample, where the evidence is assessed on the basis of probabilities. If we fail to reject the null hypothesis, IT DOES NOT GUARANTEE THAT THE NULL HYPOTHESIS IS TRUE. Similarly, if we reject the null hypothesis it does not mean that the null hypothesis is false. It is possible to get unusual data. For example, it is possible to toss ten heads in a row, although this is very unlikely.

Hypothesis testing involves two types of errors.

Type I Error: Rejecting a true null hypothesis.

$P({\rm Type\ I\ Error) = \alpha.$

Type II Error: Failing to reject a false null hypothesis.

Four scenarios can arise in a hypothesis test and are illustrated in the table below. Hypothesis tests aim to reduce Type I error, the maximum value of which is the significance level $\alpha$ .

Type I and Type II errors
	H $_0$ True	H $_0$ False
Fail to reject H $_0$	✔Correct	✘Type II Error
Reject H $_0$	✘Type I Error	✔Correct

12.4 Two-sided Tests

Here the hypotheses are

$H_0: \mu = \mu_0\quad H_1: \mu \ne \mu_0$

Example 12.2

A producer of steel cables wants to determine whether the steel cables it produces has a mean breaking strength of 5000 tonnes. An average breaking strength of less than this would not be adequate, and to produce steel cables stronger than this would incur a greater cost. A random sample of 64 cable pieces gives a sample mean breaking strength of 5158.3 tonnes with a standard deviation of 498.2 tonnes. What should the manufacturer conclude about the mean breaking strength of the cables produced, at the

5% level of significance?
1% level of significance?

Explain any difference in the two conclusions.

Solution

Let $\mu$ denote the mean breaking strength of the cables. The hypotheses are

$H_0: \mu = 5000 \quad H_1: \mu \ne 5000.$

The test statistic is

$T = \frac{\overline X - \mu}{S/\sqrt{100}} \overset{\cdot}{\underset{\cdot}{\sim}} t_{63},$

by CLT ( $n = 64 \ge 30$ ).

$\overline x = 5158.3, s = 498.2$ , so

$t_{obs} = \frac{5158.3 - 5000}{498.2/\sqrt{64}} = 2.54.$

$p-value = P(|T| > 2.54) = 0.0136.$

The p-value < 0.05, so there is sufficient evidence to reject the null hypothesis. We conclude, based on this analysis, that the mean breaking strength is not 5000 tonnes. Since the observed mean is more than 5000, we conclude that the mean breaking strength of the cables is more than 5000 tonnes.
The p-value > 0.01, so there is insufficient evidence to reject the null hypothesis. We conclude, based on this analysis, that the mean breaking strength of the cables is not different from 5000 tonnes.

The conclusions are different due to the two different significance levels.

Note:

It is always better to perform a one-sided test if the expected change is known.
In the second part of the above example, the p-value 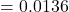$= 0.0136$ is only just greater than 1%, so evidence in favour of the null hypothesis is not very strong. If possible, the test should be repeated with a new sample.
The hypotheses again come from the problem statement. Typical wording and interpretation is given in the table below.

Typical wording

Hypothesis

Interpretation

not exceeding

safe level

is better than

${\rm H{_0}: \mu = \mu_0$

${\rm H}_1: \mu > \mu_0$

ONE-SIDED TEST

(UPPER TAIL)

is at least

not less than

minimum

${\rm H{_0}: \mu = \mu_0$

${\rm H}_1: \mu < \mu_0$

ONE-SIDED TEST

(LOWER TAIL)

no change

any difference

is equal to

${\rm H{_0}: \mu = \mu_0$

${\rm H}_1: \mu \ne \mu_0$

TWO-SIDED TEST

(UPPER TAIL)

Formulating hypotheses based on word description.

4. For two-sided tests we usually use a significance level of $\alpha = 0.05$ if no value is specified. For one-sided (or one-tail) tests we use half of this, i.e., use $\alpha = 0.025$ if no value is specified. Obviously the p-value for a one-sided test is half that for a two-sided test, and the default significance levels are also related in the same way.

5. Hypothesis tests and confidence intervals are related.

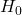$H_0: \mu = \mu_0 \quad H_1: \mu \ne \mu_0$ . If $H_0$ is rejected at significance level 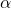$\alpha$ , then a 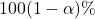$100(1-\alpha)\%$ CI will not contain 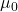$\mu_0$ . Similarly, if we fail to reject 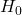$H_0$ at significance level 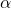$\alpha$ then a 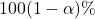$100(1-\alpha)\%$ CI will contain $\mu_0$ .
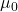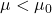$H_0: \mu = \mu_0 \quad H_1: \mu > \mu_0$ or $\mu < \mu_0$ (at sig. level 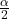$\frac{\alpha}{2}$ ). If we (fail to) reject 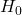$H_0$ , then a 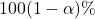$100(1-\alpha)\%$ CI (will) will not contain $\mu_0$ .

6. Implications of the conclusion of the hypothesis test should be discussed in context of the problem. This is usually in terms of opportunities, action plan, or simply rationalising/ explaining/ understanding the result.

7. Consequences of the appropriate (Type I or Type II) error should also be considered as part of the inference process.

8. Statistical significance does not imply scientific/medical/business significance. For example, suppose a drug reduces cholesterol by 0.1 and the result is statistically significant. This decrease is too small to be of any medical benefit. So while the result is statistically significant it has no medical significance.

Example 12.3

It is believed that the mean plasma aluminium level for population of healthy infants is 4.13 micro gram/l and this level increases for infants receiving antacid containing aluminium. To test this claim, a random sample of 11 infants receiving antacid containing aluminium was examined and gave a sample mean of $\overline x= 5.20$ and sample standard deviation of $s = 1.13$ (both are in micro gram/l). Test this claim at the 2.5% level of significance. State any assumptions of your analysis. What are the medical implications of the conclusion?

Solution

Let $\mu$ denote the mean plasma aluminium in healthy infants. The hypotheses are

$\mu = 4.13 \quad H_1: \mu > 4.13.$

The test statistic is

$T = \frac{\overline X - \mu}{S/\sqrt{11}} \overset{\cdot}{\underset{\cdot}{\sim}} t_{10},$

where we have assumed that the plasma aluminium levels are normally distributed.

$\overline x = 5.20, s = 1.13$ , so

$t_{obs} = \frac{5.20 - 4.13}{1.13/\sqrt{11}} = 3.1405.$

$p-value = P(T > 3.1405) = 0.0008 < 0.025$

so we have overwhelming evidence against the null hypothesis. We conclude, based on this analysis, that the mean plasma aluminium level in infants receiving antacid containing aluminium is more than 4.13.

The medical implication of this study is that if infants are given aluminium in some form then the mean aluminium level increases. That is, if infants are exposed to an environment containing aluminium then this is detrimental to their health.

12.5 Hypothesis Tests for Population Proportion

The method here is similar to that of Chapter 4.10. Let the random variable $X$ denote the number of successes in $n$ independent Bernoulli trials. Let $p$ denote the probability of success. We want to conduct hypothesis tests for $p$ . The test statistic is $X \sim$ Bin $(n,p)$ , with observed value $x_{\textrm{obs}}$ , the observed number of successes in the $n$ trials. The null hypothesis is always simply

$H_0: p = p_0.$

The alternative hypothesis and corresponding p-value is one of the following.

$\begin{align*} H_1: p < p_0 \quad & p-value = P(X \le x_{obs})\\ H_1: p > p_0 \quad & p-value = P(X \ge x_{obs})\\ H_1: p \ne p_0 \quad & p-value = 2P(X \ge x_{obs}) \quad {\textrm\ OR\ } \quad 2P(X \le x_{obs}), \end{align*}$

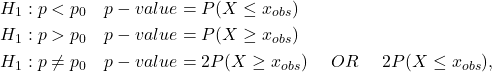
depending on which tail $x_{\textrm{obs}}$ is in.

Example 12.4

A pizza delivery shop advertises that it will deliver pizzas in the local area within half an hour of ordering or the pizza is free. The manager feels that this marketing idea will be profitable as long as at least 90% of the deliveries are within the time. To test if this is the case, the manager takes a random sample of 20 deliveries and finds that 16 were delivered on time.
(a) What should the manager conclude about the proportion of pizzas that are delivered within the required time?

(b) What are the consequences of a Type I error?

(c) Which is worse, a Type I error or a Type II error?

Solution

Let $p$ denote the proportion of pizzas delivered in time and let the random variable $X$ denote the number of pizzas delivered in time. Then $X \sim Bin(20,p)$ .

(a)The hypotheses of interest are:

$H_0: p = 0.9 \quad H_1: p < 0.9.$

The p-value is

$p-value = P(X \le 16|p = 0.9) = 0.1330 > 0.025,$

so there is insufficient evidence to reject the null hypothesis at the 2.5% level of significance. We conclude that at least 90% of the pizzas are delivered in time.

(b) Type I Error occurs when a true null hypothesis is rejected. In this case either the delivery time will be increased or more resources will be spent on trying to reduce delivery time. The former is damaging to market perception, and the latter, while improving business, is needless.

(c) Type II Error occurs when a false null hypothesis is not rejected. In this $p < 0.9$ but the business believes that $p$ is at least 0.9. So more free pizzas will be delivered, which is bad for business. In this case Type II Error is worse as it will cost the business.

Example 12.5

Arthritis is a painful, chronic inflammation of the joints. An experiment on the side effects of pain relievers examined arthritis patients to find the proportion of patients who suffer side effects when using ibuprofen to relieve the pain. If more than 3% of users suffer side effects, the Food and Drug Administration (FDA) will put a stronger warning label on packages of ibuprofen. 440 subjects with chronic arthritis were given ibuprofen for pain relief; 23 subjects suffered from adverse side effects.
(a) What action should the FDA take?
(b) What assumptions are required in your analysis?
(c) Which is worse in this case, Type I or Type II error?

Solution

Let the the random variable $X$ denote the number of patients out of 440 who suffer side effects when using ibuprofen for pain relief. Then $X \sim {\rm Bin}(440, p)$ , where $p$ denotes the proportion of arthritis patients who suffer side effects when using ibuprofen for pain relief.

(a) The hypotheses of interest are

$H_0: p = 0.03 \quad H_1: p > 0.03.$

The test statistic is $X \sim {\rm Bin}(440, p)$ , with observed value $x_{obs} = 23$ , so the p-value is

$p-value = P(X \ge 23|p = 0.03) = 0.0080 < 0.025$

so there is very strong evidence against the null hypothesis. We conclude that the proportion of patients who suffer side effects is more than 3% and the FDA should put a stronger warning label on the package.

(b) We assume that the probability of side effects is the same for each patient and the occurrence of side effects in patients is independent.

(c) Type I Error: rejecting a true null hypothesis; Type II Error: failing to reject a false null hypothesis. In this case type II Error is more serious, as in this case the proportion of patients with side effects is more than 3% but we conclude the opposite. Thus no stronger warning label will be put on and patients will continue to experience side effects.

Hypothesis tests for Population Proportion: Using Normal Approximation

We note that in Chapter 10 the distribution of the sample proportion was obtained as approximately normal for larger sample size ( $n \ge 30$ ) by the Central Limit Theorem. Then the standardised sample proportion is approximately distributed as the standard normal distribution. So we could base the hypothesis tests for population proportion on the normal distribution.

Then the test statistic is

$Z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}} \overset{\cdot}{\underset{\cdot}{\sim}} {\rm N}(0,1)$

by CLT.

The observed value of test statistic is

$z_{\textrm{obs}}=\frac{\hat{p}_{\rm obs}-p}{\sqrt{\frac{\hat{p}_{\rm obs}(1-\hat{p}_{\rm obs})}{n}}} \overset{\cdot}{\underset{\cdot}{\sim}} {\rm N}(0,1)$

The null hypothesis is always simply

$H_0: p = p_0.$

The alternative hypotheses and the corresponding p-value is one of the following.

$\begin{align*} H_1: p < p_0 & \quad p-value = P(Z \le z_{\textrm{obs}})\\ H_1: p > p_0 & \quad p-value = P(Z \ge z_{\textrm{obs}})\\ H_1: p \ne p_0 & \quad p-value = P(|Z| \ge |z_{\textrm{obs}}|) \end{align*}$

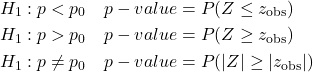
Example 12.6

Repeat the hypothesis test in Example 12.5 using the normal approximation.

Solution

Let the the random variable $X$ denote the number of patients out of 440 who suffer side effects when using ibuprofen for pain relief. Then $X \sim Bin(440, p)$ , where $p$ denotes the proportion of arthritis patients who suffer side effects when using ibuprofen for pain relief.

The hypotheses of interest are

$H_0: p = 0.03 \quad H_1: p > 0.03.$

The observed sample proportion is

$\hat p = \frac{23}{440} = 0.05227.$

The corresponding observed standard error is

$Se(\hat p) = \sqrt{\frac{0.05227(1-0.05227)}{440}} = 0.01061.$

The observed value of the standardised sample proportion is

$z_{obs} = \frac{0.05227 - 0.03}{0.01061} = 2.099.$

The p-value of the test is

$p-value = P(Z > 2.099) = 0.0179 < 0.025$

so we have sufficient evidence to reject the null hypothesis.

Note

The p-value here is much larger (almost twice) than that obtained in Example 12.5, but the conclusion is the same. It is conceivable that in some cases the conclusions using the two different methods could be different and can lead to different conclusions.
In practice, given the power of computation packages, there is no need to use the normal approximation for these types of problems.

12.6 Confidence Intervals for Binomial proportion

In Chapter 10 we obtained confidence intervals for the binomial proportion based on the normal approximation. In R we can compute exact confidence intervals using various packages. An example is given below, where we compute a 95% confidence interval for the data in Example 12.5.

We use the package GenBinomapps.

library(GenBinomApps)
> clopper.pearson.ci(k = 23, n = 440, alpha = 0.05, 
      CI = "two.sided")
 Confidence.Interval Lower.limit Upper.limit alpha
           two.sided  0.03342135  0.07740489  0.05

The calculated confidence interval is (0.0334, 0.0774). Using the normal approximation:

$(0.05227 - 1.96\times 0.0106, 0.05227 +1.96\times 0.0106) = (0.0315, 0.0731).$

Again note the difference in the confidence intervals. While for most applications the difference is tolerable, in some cases the differences could lead to incorrect conclusions.

12.7 Summary

Understand the steps in hypothesis testing.
Note that statistical significance does not imply a significant result in the context.
Understand the consequences of Type I and Type II error.
For small sample sizes test for population mean needs to assume that the data is from a normally distributed population.
For binomial proportion one can use the binomial distribution for both hypothesis tests and calculation of confidence intervals. While the normal approximation can also be used, there is no need for this given the availability of computation packages. In addition, the normal approximation may in some cases give an incorrect conclusion.

Licence

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

12 One Sample Hypothesis Tests

Learning Outcomes

Contents

12.1 Introduction

12.2 Hypothesis Tests for Population Mean

Method

Rationale

Notes

12.3 Type I and Type II Errors

12.4 Two-sided Tests

Note:

12.5 Hypothesis Tests for Population Proportion

Hypothesis tests for Population Proportion: Using Normal Approximation

Note

12.6 Confidence Intervals for Binomial proportion

12.7 Summary

Licence

Share This Book