5 Continuous Random Variables
Learning Outcomes
At the end of this chapter you should be able to:
- explain the concept of a continuous random variable;
- work with probability density functions and cumulative distribution functions;
- understand the concept of a uniform distribution;
- compute expectations and variances in simple cases;
- be able to compute the mean and variance of a uniform distribution using appropriate formulae.
5.1 Introduction
Discrete random variables take values that form a finite set, or a set that can be listed. Continuous random variables take values in a given interval. For example, let the rv
![]() denote the time it takes to the next failure of a machines. Then
denote the time it takes to the next failure of a machines. Then ![]() takes all values
takes all values
![]() . Now
. Now ![]() , since this is just one of infinitely many values.
, since this is just one of infinitely many values.
As another example, what is the probability that I hit exactly the centre of a dart board. This is just one point of infinitely many, so this probability is zero.
Continuous random variables do not have probability mass functions. Instead we evaluate probabilities for intervals.
Notation
The interval ![]() is called a closed interval, as it contains both its end points. We use the notation
is called a closed interval, as it contains both its end points. We use the notation ![]() to denote this. We represent this on a number line by closed circles at both ends.
to denote this. We represent this on a number line by closed circles at both ends.
The intervals
![]() is a semi-closed or semi-open interval, as it contains only one end point. The number line representation has a closed circle at the closed end and an open circle at the open end.
is a semi-closed or semi-open interval, as it contains only one end point. The number line representation has a closed circle at the closed end and an open circle at the open end.
The interval ![]() is an open interval, as it contains neither end point. The number line representation has open circles at both ends.
is an open interval, as it contains neither end point. The number line representation has open circles at both ends.
5.2 Probability density function
The probability density function (pdf) ![]() for a continuous random variable
for a continuous random variable ![]() is a function that satisfies
is a function that satisfies
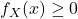 or all values of
or all values of 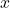 ,
,- the total area under the graph of
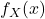 is
is  ,
, -
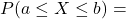 area under the graph of
area under the graph of 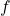 between
between  and
and 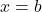 .
.
In the examples we consider the areas will be calculated using geometry. Students who know calculus can obtain the probabilities (areas) by integration. Thus
![]()
Example 5.1
A random variable ![]() has pdf
has pdf
![Rendered by QuickLaTeX.com \[f_X(x) = \begin{cases} x, & 0 \le x \le B\\ 0, & {\rm otherwise} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-2c0891bdfb01fb2ef8635bcda20775a1_l3.png)
(a) Find the value of ![]() .
.
(b) Evaluate
(i) ![]() ,
, ![]()
(ii) ![]() ,
, ![]()
(iii) ![]() .
.
Solution
First we plot a graph of the probability density function. This is given below, with some areas highlighted (for later parts).
(a) The total area under the graph is 1. This is simply the area of a triangle, so
![]()
(b) (i) ![]() .
.
(ii) We can calculate the required probability as the area of a trapezium, given by the average of the parallel sides times the vertical distance between them.
![]()
Alternativley,
![]()
(iii) ![]() , as this is the area under a single point.
, as this is the area under a single point.
Note for continuous random variables, since the area under a point is zero, ![]() .
.
Example 5.3: THE UNIFORM DISTRIBUTION
The random variable ![]() has a uniform distribution on the interval
has a uniform distribution on the interval ![]() ,
, ![]() , if its pdf is
, if its pdf is
![Rendered by QuickLaTeX.com \[f_X(x) = \begin{cases} \frac{1}{b-a}, & a \le x \le b\\ 0, & \text\ otherwise. \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-af3ead5fe37d2e021bfeae6e2d1f728c_l3.png)
The total area under the graph is 1, and this determines the height of the graph.
Then
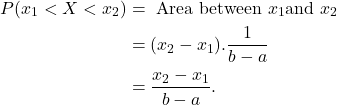
5.3 Cumulative distribution function
For continuous random variables, these probabilities are computed as an area, so
![]()
Example 5.4: U[0,1]
We determine the CDF piecewise.
For ![]() ,
, ![]() .
.
For ![]() ,
, ![]()
For ![]() ,
, ![]() .
.
![Rendered by QuickLaTeX.com \[F_X(x) = \begin{cases} 0, & x<0\\ x, & 0 \le x < 1\\ 1, & x \ge 1. \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-ef027d6bd7dc2f8361180c331b49f206_l3.png)
Exercise
For ![]() random variable, show that the cdf is given by
random variable, show that the cdf is given by
![Rendered by QuickLaTeX.com \[F_X(x) = \begin{cases} 0, & x < a\\ \frac{x-a}{b-a}, & a \le x < b\\ 1, & x \ge b. \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-111bb929a2b6d713eaac414d6d45aa17_l3.png)
and sketch it.
5.4 Expectation ◊
If ![]() is a function of
is a function of ![]() then for a random variable
then for a random variable ![]()
![]()
[Compare with a discrete random variable ![]() :
: ![]() ]
]
Example 5.5: ![]()
For ![]() ,
,
![]()
and
![]()
so the standard deviation is
![]()
Proof
Exercise.
Example 6.6
For ![]() , the mean is
, the mean is
![]()
and the variance is
![]()
so the standard deviation is
![]()

