8 The Normal Distribution
Learning Outcomes
At the end of this chapter you should:
- understand the concept of a normal random variable;
- be able to calculate probabilities for a standard normal distribution;
- be able to solve problems based on general normal distributions;
- be able to model and solve problems involving sums and differences of normal distributions;
- be able to compute probabilities for a binomial distribution using an appropriate normal approximation;
- be able to model and solve problems using a combination of continuous and discrete random variables as appropriate.
8.1 Introduction
The normal distribution is a very important and often used continuous distribution.
|
Standardisation
|
Probability density function—effect of changing the mean
Below are sketched the pdfs of the normal distributions for different values of the mean. Note the effect of changing the mean. The shape of the curve is unchanged, but the central location changes. Note that in each case the curve is symmetric about its mean.
Probability density function—effect of changing the standard deviation
Sketched below are the pdfs of the normal distributions for different values of the variance. Note the effect of changing the variance. The central location (line of symmetry) of the curve is unchanged, but the curve is wider if the variance is larger. Here the mean is 0, and the all the curves have ![]() as the line of symmetry.
as the line of symmetry.
Normal distribution tables
Tables list cumulative probabilities for the standard normal distribution. We will illustrate the use of tables by examples. Note that normal probabilities can be easily obtained using software such as R. Several types of tables are available for the standard normal distribution. We will use the one given below. (This table is also available for download.)
The table gives ![]() for
for ![]() . Note that
. Note that ![]() , so we can obtain
, so we can obtain
![]()
8.2 Normal distribution problems
For ![]() , there are usually two types of problems.
, there are usually two types of problems.
- Obtain the probability that
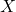 lies in a given interval.
lies in a given interval. - Given a probability, find the corresponding interval for
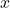 (the inverse problem).
(the inverse problem).
Symmetry of the standard normal distribution about 0 will be used often. The examples below illustrate the ideas.
Example 8.1
Let ![]() . Determine the following.
. Determine the following.
(i) ![]()
Solution
![]()
Using R,
> pnorm(1)
[1] 0.8413447
(ii) ![]()
Solution
By symmetry, as illustrated in the graph above,
![]()
Using R,
> pnorm(-1)
[1] 0.1586553
(iii) ![]() .
.
Solution
![]()
Using R,
> pnorm(1, lower.tail = F)
[1] 0.1586553
(iv) ![]()
Solution
![]()
Using R,
> pnorm(2.51, lower.tail = F)
[1] 0.006036558
(v) ![]()
Solution
![]()
Using R,
> pnorm(1.96) - pnorm(-1.96)
[1] 0.9500042
(vi) The value of ![]() such that
such that ![]()
Solution
We need to look up the value of the probability in the tables, and then read the value of ![]() it corresponds to. This gives
it corresponds to. This gives ![]() , obtained by interpolation between the neighbouring values. Alternatively, at the bottom of the tables are listed critical points of the normal distribution. This table lists the values of
, obtained by interpolation between the neighbouring values. Alternatively, at the bottom of the tables are listed critical points of the normal distribution. This table lists the values of ![]() corresponding to often-used right tail probabilities. Here since
corresponding to often-used right tail probabilities. Here since ![]() , the right tail probability is
, the right tail probability is ![]() . From the critical points table the value of
. From the critical points table the value of ![]() this corresponds to is 1.645.
this corresponds to is 1.645.
Using R,
> qnorm(0.95)
[1] 1.644854
(vii) The value of ![]() such that
such that ![]()
Solution
Now, as shown in the graph, the probability between ![]() and
and ![]() is 0.95. Then the two tail probabilities are a total of 0.05. By symmetry, the each tail contains a probability of 0.025. From the table of critical values we get
is 0.95. Then the two tail probabilities are a total of 0.05. By symmetry, the each tail contains a probability of 0.025. From the table of critical values we get ![]() .
.
Using R, we need to consider the probability in the lower tail. Note that the in the figure above, the missing tail probability (the unshaded area) is 0.025 in the lower tail (and the same in the upper tail). Then the we need the value of ![]() such that
such that ![]() . This is the probability we look up in R.
. This is the probability we look up in R.
> qnorm(0.975)
[1] 1.959964
(viii) ![]()
Solution
Note
![]()
and
![]()
so the required probability is ![]() .
.
Using R,
> pnorm(2.7) - pnorm(-1.5)
[1] 0.9297258
Non-standard normal distribution
Probabilities for non-standard normal distributions can be easily obtained using software. Here we illustrate the method using tables. The method is also useful in other contexts, so it is still worth understanding.
Let ![]() . Then using the standardisation results,
. Then using the standardisation results,
![]()
The following examples illustrate the ideas.
Example 8.2
Let ![]() . Determine the following.
. Determine the following.
(i) ![]() .
.
Solution
We standardise ![]() by subtracting its mean and dividing by the standard deviation. Put
by subtracting its mean and dividing by the standard deviation. Put
![]()
Then
![]()
Using R, we do not need to work with the standardised normal distribution, as we can simply specify the mean and standard deviation in the R function.
> pnorm(0, mean = 5, sd = 4)
[1] 0.1056498
(ii) ![]() .
.
Solution
![]()
Using R,
> pnorm(10, mean = 5, sd = 4, lower.tail = F)
[1] 0.1056498
(iii) ![]() .
.
Solution
We standardise both ends.
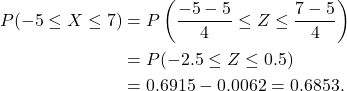
Using R,
> pnorm(7, mean = 5, sd = 4) - pnorm(-5, mean = 5, sd = 4)
[1] 0.6852528
(iv) The value of ![]() such that
such that ![]() .
.
Solution
We know that ![]() , so
, so
![]()
Example 8.3
Let ![]() , and suppose
, and suppose ![]() . Find the value of
. Find the value of ![]() .
.
Solution
![]()
Now ![]() , so
, so
![]()
Example 8.4
A machine fills bottles of soft drink to a mean volume of 210 ml with a standard deviation of 10 mL. The label on the bottle specifies a volume of 200 ml. A bottle is under-filled if it contains less than the labelled volume. Assume that the volumes of the bottles are normally distributed.
(a) What percentage of bottles are under-filled?
(b) In order to reduce the percentage of under-filled bottles to 1% the company decides
to adjust the standard deviation of the volumes filled by the machine. What should
the standard deviation be reduced to?
Solution
(a) Let the random variable ![]() denote the volume of a botte of soft drink. Then
denote the volume of a botte of soft drink. Then ![]() .
.
![]()
that is, 15.9%.
Using R,
> pnorm(200, mean = 210, sd = 10)
[1] 0.1586553
(b) Now ![]() . Then
. Then
![]()
Now ![]() , so
, so
![]()
that is the standard deviation should be reduced to 4.30 ml.
8.3 SUM of Normal Random Variables
Result
Let ![]() ,
, ![]() and put
and put ![]() . Then
. Then ![]() , where
, where
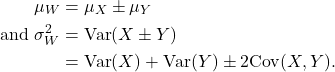
If ![]() and
and ![]() are independent, then
are independent, then ![]() , so
, so
![]()
This result can be extended to a sum of several independent normal random variables.
Example 8.5
Vasilopoulos et al. (2020) investigated the length of the femur in human males and females. They results are tabulated below, for the right male and female femur.
| Male | Female | |
|---|---|---|
| Mean (cm) | 43.04 | 39.90 |
| Standard Deviation (cm) | 2.32 | 2.40 |
What is the probability that a randomly selected male right femur is longer than a randomly selected female right femur?
Reference: Vasilopoulos A, Tsoucalas G, Panagouli E, Trypsianis G, Thomaidis V, Fiska A. (2020). Odontoid Process and Femur: A Novel Bond in Anatomy. Cureus, 12(3):e7372. https://doi.org/10.7759/cureus.7372
Solution
Let the random variables ![]() and
and ![]() denote the length of the right femur bone of a male and female respectively. Then
denote the length of the right femur bone of a male and female respectively. Then ![]() and
and ![]() . Put
. Put ![]() . Then
. Then
![]()
Then ![]() . Note that we have assumed that the lengths of the femurs of the males and females are independent. We need
. Note that we have assumed that the lengths of the femurs of the males and females are independent. We need
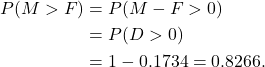
Note that we obtained the probability directly from R, using
> pnorm(0,3.14, sqrt(11.1424), lower.tail = F)
[1] 0.38265647
Example 8.6
A machine makes washers with hole diameters that are normally distributed, with mean 15.2 mm and variance 0.03 mm![]() . Another machine makes bolts with diameters that are normally distributed, with mean 15.0 mm and variance 0.01 mm
. Another machine makes bolts with diameters that are normally distributed, with mean 15.0 mm and variance 0.01 mm![]() .
.
(a) What is the probability that a randomly selected bolt will fit through a randomly selected washer?
(b) What should the mean diameter of the washer holes be if 99% of the bolts are to fit the washers?
Solution
Let the random variables ![]() and
and ![]() denote the diameters of a randomly selected washer and bolt respectively. Then
denote the diameters of a randomly selected washer and bolt respectively. Then ![]() . Further, let
. Further, let ![]() , so
, so ![]() .
.
(a)
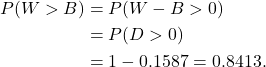
Again we obtained the probability ![]() directly from R using
directly from R using
> pnorm(0,0.2, sqrt(0.04))
[1] 0.1586553
(b) Now ![]() , so
, so ![]() , and
, and
![]()
Since ![]() , we have
, we have
![]()

