7 Contingency Tables
Learning Outcomes
At the end of this chapter you should be able to:
- understand what a contingency table is;
- perform a chi squared test of independence for a contingency table;
- determine if two categorical variables are independent in a contingency table context;
- determine the form of dependence if any in a contingency table;
- explain your findings clearly.
Contents
7.1 Introduction
Inference for categorical or counts data was briefly covered in inference for population proportions and Poisson mean. We now consider categorical data in more detail and greater generality.
We consider the situation where two categorical variables are involved, and a joint table of observed frequencies is available. This is called a contingency table. We analyse the data for association between the variables, that is, we want to investigate if the variables are independent.
Such data often arises from a survey.
Example 7.1
A manufacturing facility has three different production lines, each of which produces the same product. The production manager wants to know if the proportion of defectives is the same for each production line. Data from each production line was collected, and is summarised in the table below.
| Production line | A | B | C | Row Total |
|---|---|---|---|---|
| Defective | 12 | 22 | 14 | 48 |
| Good | 188 | 148 | 196 | 532 |
| Column total | 200 | 170 | 210 | 580 |
At the 5% level of significance, determine if the proportion of defectives is the same for each production line.
Method
- Given a table of observed counts
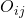 in row
in row 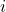 and column
and column 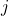 , we compute the expected counts
, we compute the expected counts 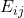 under the null hypothesis.
under the null hypothesis. - We then compute a test statistic based on the difference between the observed frequencies and the expected frequencies.
- We require that the expected frequency in each cell is at least 5; otherwise adjacent cells are pooled (merged, combined) until this requirement is satisfied.
The hypotheses
Here we are testing the hypotheses
![]()
The observed frequency in each cell of the table is found assuming the null hypothesis to be true, that is, under the assumption of independence.
7.2 General Contingency Table
| col |
Row Total | |||
| row |
||||
| Column Total | T |
We use ideas from joint distributions (see Chapter 6).
If the total of row ![]() is
is ![]() , the total of column
, the total of column ![]() is
is ![]() and the grand total is
and the grand total is ![]() , then the probability of being in row
, then the probability of being in row ![]()
![]()
the probability of being in column ![]() is
is
![]()
so, assuming independence, the probability of being in cell ![]() is
is
![]()
Then the expected frequency of cell ![]() is
is
![]()
Test Statistic
![Rendered by QuickLaTeX.com \[X^2 = \sum_{i=1}^r\sum_{j=1}^c\frac{\left(o_{ij}-e_{ij}\right)^2}{e_{ij}},\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-b8ca7267368df570bd0f33052893ebd3_l3.png)
and this has a chi-squared distribution with degrees of freedom ![]() , denoted
, denoted ![]() , where the degrees of freedom is given by
, where the degrees of freedom is given by
![]()
where ![]() and
and ![]() are the number of rows and columns respectively.
are the number of rows and columns respectively.
Example 7.1
A manufacturing facility has three different production lines, each of which produces the same product. The production manager wants to know if the proportion of defectives is the same for each production line. Data from each production line was collected, and is summarised in the table below.
| Production line | A | B | C | Row Total |
|---|---|---|---|---|
| Defective | 12 | 22 | 14 | 48 |
| Good | 188 | 148 | 196 | 532 |
| Column total | 200 | 170 | 210 | 580 |
At the 5% level of significance, determine if the proportion of defectives is the same for each production line.
Solution
The hypotheses of interest are
![]() Proportion of defectives is independent of machine (that is, the proportion of defectives is the same for all the machines).
Proportion of defectives is independent of machine (that is, the proportion of defectives is the same for all the machines).
![]() is false.
is false.
The table below shows the expected frequencies (in brackets) for each cell under the null hypothesis, that is, under the assumption of independence. Note that these expected frequency sum to give the same row and column totals.
| Production line | A | B | C | Row Total |
|---|---|---|---|---|
| Defective | 12 (16.55) | 22 (14.07) | 14 (17.38) | 48 |
| Good | 188 (183.45) | 148 (155.93) | 196 (192.62) | 532 |
| Column total | 200 | 170 | 210 | 580 |
We provide the calculations for the expected frequencies for the first row to illustrate the process.
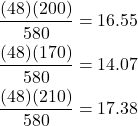
Exercise 7.1
Calculate the remaining expected frequencies.
The observed value of the test statistic is
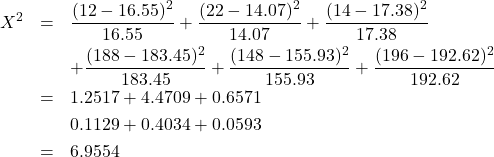
The degrees of freedom for the chi squared distribution is ![]() , and the p-value for the test is
, and the p-value for the test is
![]()
(from R), where ![]() , so we reject the null hypothesis at the 5 % level of significance. We conclude that the data provides evidence that the proportion of defectives is not the same for the production lines. A plot of the
, so we reject the null hypothesis at the 5 % level of significance. We conclude that the data provides evidence that the proportion of defectives is not the same for the production lines. A plot of the ![]() is shown below, with the 5% upper tail shaded.
is shown below, with the 5% upper tail shaded.
We would also like to identify which production line is producing the higher proportion of defectives. In fact, looking that the chi square calculations, the largest contribution is in the cell corresponding to production line B Defectives. Examining the expected frequencies shows that it has a much higher number of defectives than that expected under the null hypothesis. Thus we conclude that production line 2 produces a higher proportion of defectives than the other two machines.
Exercise 7.2
A mobile technology provider has three different locations set up to provide customers with technical support for their products. The management wants to identify the call centre with the highest proportion of unsuccessfully resolved calls. They randomly select logs from each location and collect the following data.
| Call centre | A | B | C | Row Total |
|---|---|---|---|---|
| Successful | 257 | 264 | 283 | 804 |
| Unsuccessful | 43 | 86 | 97 | 226 |
| Column total | 300 | 350 | 380 | 1030 |
Based on this data, what should management conclude?
7.3 Analysis of contingency tables in R
The R code below is for the analysis for the data of Exercise 7.2.
The output gives the observed value of the test statistic and the p-value. The hypothesis test is conducted using the p-value; in this case the p-value ![]() , so there is sufficient evidence to reject the null hypothesis.
, so there is sufficient evidence to reject the null hypothesis.
M <- as.table(rbind(c(257, 264, 283), c(43, 86, 97))) dimnames(M) <- list(Calls = c("Successful", "Unsuccessful"), Location = c("1","2", "3")) (Xsq <- chisq.test(M)) # Prints test summary #Enclosing a command in brackets runs the command and also prints out the output. Pearson's Chi-squared test data: M X-squared = 14.404, df = 2, p-value = 0.0007453 Xsq$observed # observed counts (same as M) Location Calls 1 2 3 Successful 257 264 283 Unsuccessful 43 86 97 Xsq$expected # expected counts under the null hypothesis of independence or no association Location Calls 1 2 3 Successful 234.17476 273.20388 296.62136 Unsuccessful 65.82524 76.79612 83.37864 Xsq$residuals # Pearson residuals Location Calls 1 2 3 Successful 1.4915759 -0.5568365 -0.7908957 Unsuccessful -2.8133202 1.0502713 1.4917397 Xsq$stdres # standardized residuals Location Calls 1 2 3 Successful 3.782396 -1.463040 -2.125424 Unsuccessful -3.782396 1.463040 2.125424
Note that the output contains (Pearson and standardised) residuals which makes it easier to determine any associations in the data. From this, we see that the centres with the largest (Pearson and standardised) residuals are 1 for successful calls and 3 for unsuccessful calls. So centre 1 is identified as having more successfully resolved calls than expected under independence, and centre 3 has more unsuccessfully resolved calls.

