6 Joint Distributions
Learning Outcomes
At the end of this chapter you should be able to:
- explain the concept of a joint distribution;
- work with joint probability mass functions;
- compute expectations, variances and covariances and know their properties;
- determine if two jointly distributed random variables are independent;
- determine the mean and variance of a sum of random variables;
- compute the correlation coefficient between two jointly distributed random variables, and know its properties.
6.1 Introduction
Frequently two or more variables are related and may change together.
Examples are:
- Blood pressure and Sugar level
- Prey and Predator numbers
- Percentage Forest cover and Rainfall
Notation
We use the notation ![]() to denote the joint probability mass function of random variables
to denote the joint probability mass function of random variables ![]() and
and ![]() , where
, where
![]()
The joint pmf can be tabulated, and is the usual way of presenting the joint pmf of a pair of discrete random variables. The example below illustrates the ideas.
Joint probability mass function
We consider two random variables that that change together. Their joint pmf can be presented as a table, given below.
| -1 | 0 | 1 | |||
|---|---|---|---|---|---|
| 0 | 0.1 | 0.05 | 0.2 | 0.35 | |
| 1 | 0.05 | 0.1 | 0.1 | 0.25 | |
| 2 | 0.15 | 0.05 | 0.2 | 0.4 | |
| 0.3 | 0.2 | 0.5 | 1 | ||
The table gives joint probabilities. Thus for example,
![]()
Note that ![]() is a probability mass function, so it satisfies:
is a probability mass function, so it satisfies:
![]()
for each value of ![]() and each value of
and each value of ![]() , and
, and
![]()
The marginal pmfs of ![]() and
and ![]() are obtained by appropriately summing the rows (giving the pmf of
are obtained by appropriately summing the rows (giving the pmf of ![]() ) and columns (giving the pmf of
) and columns (giving the pmf of ![]() ) of the joint table. This follows from the theorem of total probabilities. Thus for example,
) of the joint table. This follows from the theorem of total probabilities. Thus for example,
![]()
Example 6.1
Parent-offspring always share exactly one allele identical by descent (IBD), while siblings can share 0, 1 or 2. The table below gives the joint genotype distribution for IBD status for two siblings.
| Sibling 1 |
|||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | |||
| Sibling 2 |
0 | 0.125 | 0.25 | 0.0625 | 0.4375 |
| 1 | 0. | 0.25 | 0.125 | 0.375 | |
| 2 | 0 | 0.125 | 0.0625 | 0.1875 | |
| 0.125 | 0.625 | 0.25 | 1 | ||
(a) What is the probability that
(i) Sibling 1 has more alleles than sibling 2?
(ii) the total number of alleles for the two siblings is more than 2?
(b) What is expected total number of alleles for the siblings?
Solution
(a) (i) ![]() The cells this corresponds to are highlighted in mauve.
The cells this corresponds to are highlighted in mauve.
(ii) The total is ![]() . The three cells that correspond to
. The three cells that correspond to ![]() are underlined. Then
are underlined. Then
![]()
(b) We need ![]() . First we obtain
. First we obtain ![]() . This is obtained by multiplying the values of
. This is obtained by multiplying the values of ![]() (first row of table) with the corresponding marginal probabilities (bottom row of table) and summing the results.
(first row of table) with the corresponding marginal probabilities (bottom row of table) and summing the results.
![]()
Similarly,
![]()
Then
![]()
Note
In general, if ![]() is a function of
is a function of ![]() and
and ![]() , we can compute
, we can compute ![]() by
by
![]()
Thus in the above example,
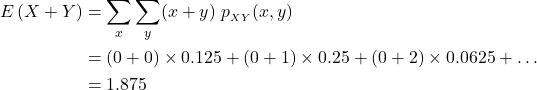
as previously.
Exercise
For Example 6.1, calculate ![]() .
.
[Ans: 1]
6.2 Independent random variables
Two random variables ![]() and
and ![]() are independent if
are independent if
![]()
for each value of ![]() and
and ![]() .
.
[Compare with ![]() for independent events.]
for independent events.]
Thus two random variables are independent if their joint pmf can be obtained by multiplying the marginal pmfs.
Example 6.2
(a)
| -1 | 0 | 1 | |||
|---|---|---|---|---|---|
| -2 | 0.06 | 0.04 | 0.10 | 0.20 | |
| 0 | 0.12 | 0.08 | 0.2 | 0.40 | |
| 1 | 0.12 | 0.08 | 0.2 | 0.40 | |
| 0.30 | 0.20 | 0.50 | 1 | ||
Each entry in the table is the product of the corresponding row and column totals. Thus random variables ![]() and
and ![]() are independent since
are independent since ![]() for each
for each ![]() and each
and each ![]() . In addition, any events in terms of
. In addition, any events in terms of ![]() and
and ![]() are also independent. Thus
are also independent. Thus
![]()
(b)
| -1 | 0 | 1 | |||
|---|---|---|---|---|---|
| -1 | 0.1 | 0.2 | 0.1 | 0.4 | |
| 0 | 0.1 | 0.05 | 0 | 0.15 | |
| 2 | 0.2 | 0.15 | 0.1 | 0.45 | |
| 0.4 | 0.4 | 0.2 | cx1 | ||
Random variables ![]() and
and ![]() are not independent, since for example,
are not independent, since for example,
![]()
(c) In (a) above, show that
![]()
Solution
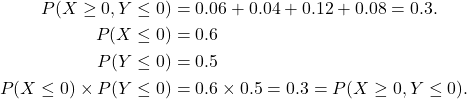
In general if ![]() and
and ![]() are independent then for any sets
are independent then for any sets ![]() and
and ![]() ,
,
![]()
[The symbol ![]() is read as “is in”.]
is read as “is in”.]
6.3 Covariance
The covariance between random variables ![]() and
and ![]() , denoted
, denoted ![]() , is defined as
, is defined as
![]()
Notes
- The covariance can be calculated from the joint distribution of
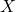 and
and 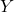 .
. 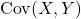 is a measure of the relationship between
is a measure of the relationship between 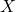 and
and 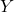 . If
. If 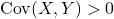 then as
then as 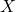 increases so does
increases so does 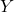 . Similarly, if
. Similarly, if 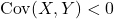 then as
then as 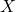 increases
increases 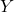 decreases.
decreases.
Theorem
![]()
Proof
![Rendered by QuickLaTeX.com \begin{align*} {\rm Cov}(X,Y) &= {\rm E}\left[(X-\mu_X)(Y-\mu_Y)\right]\\ &= {\rm E}\left[X(Y-\mu_Y) - \mu_X(Y-\mu_Y)\right]\\ &= {\rm E}(XY-\mu_Y\ X) - \mu_X\underbrace{{\rm E}(Y-\mu_Y)}_{=0}\\ &= {\rm E}(XY) - \mu_Y{\rm E}(X)\\ &= {\rm E}(XY) - \mu_X \mu_Y. \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-5852bc0c2abbd136c02514120b72781a_l3.png)
This form is simpler for calculating covariances.
Example 6.3
| -5 | 0 | 3 | |||
|---|---|---|---|---|---|
| -4 | 0.2 | 0.1 | 0.1 | 0.4 | |
| 0 | 0.05 | 0.1 | 0.05 | 0.2 | |
| 5 | 0.1 | 0.2 | 0 | ||
| 0.35 | 0.4 | 1 | |||
Find
(i) the values of ![]()
(ii) ![]()
(iii) ![]()
(iv) Cov![]()
Solution
(i) Since the probabilities in the table sum to 1, we get ![]() . The updated table is given below.
. The updated table is given below.
| -5 | 0 | 3 | |||
|---|---|---|---|---|---|
| -4 | 0.2 | 0.1 | 0.1 | 0.4 | |
| 0 | 0.05 | 0.1 | 0.05 | 0.2 | |
| 5 | 0.1 | 0.2 | 0.1 | 0.4 | |
| 0.35 | 0.4 | 0.25 | 1 | ||
(ii)
![]()
(iii)
![]()
(iv) In the calculation of ![]() , we can see that the column and row that correspond to
, we can see that the column and row that correspond to ![]() and
and ![]() respectively simplify the calculation. This leaves us with only four calculations for calculating
respectively simplify the calculation. This leaves us with only four calculations for calculating ![]() .
.
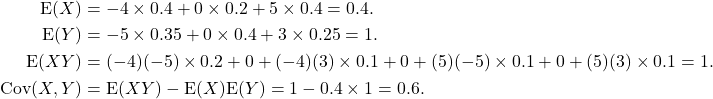
Theorem
If ![]() and
and ![]() are independent random variables then
are independent random variables then
![]()
Proof
We use the fact that if ![]() and
and ![]() are independent random variables then
are independent random variables then
![]()
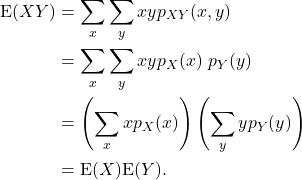
Note that in the third line we have factorised the sum into a sum involving only ![]() and another involving only
and another involving only ![]() .
.
Corollary
IF ![]() and
and ![]() are independent random variables then
are independent random variables then
![]()
Proof
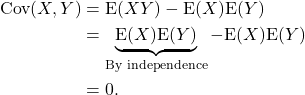
Example 6.4
As in Example 6.2(a).
| -1 | 0 | 1 | |||
|---|---|---|---|---|---|
| -2 | 0.06 | 0.04 | 0.10 | 0.20 | |
| 0 | 0.12 | 0.08 | 0.2 | 0.40 | |
| 1 | 0.12 | 0.08 | 0.2 | 0.40 | |
| 0.30 | 0.20 | 0.50 | 1 | ||
From Example 6.2 (a), ![]() and
and ![]() are independent. Verify that
are independent. Verify that
![]()
Solution
By independence,
![]() , so
, so ![]() .
.
Also, by independence ![]() .
.
Exercise
In the above example calculate ![]() directly and show that it is
directly and show that it is ![]() .
.
IMPORTANT NOTE
IF ![]() and
and ![]() are independent THEN Cov
are independent THEN Cov![]() . If Cov
. If Cov![]() then
then ![]() and
and ![]() are not necessarily independent.
are not necessarily independent.
Example 6.5
| -1 | 0 | 1 | |||
|---|---|---|---|---|---|
| 0 | 0.1 | 0 | 0.1 | 0.2 | |
| 1 | 0.1 | 0.1 | 0.1 | 0.3 | |
| 2 | 0.15 | 0.2 | 0.15 | 0.40 | |
| 0.35 | 0.3 | 0.35 | 1 | ||
It can easily be verified that
![]()
so ![]() . However,
. However, ![]() and
and ![]() ARE NOT independent, for example,
ARE NOT independent, for example,
![]()
Properties of Covariance
C1. Cov![]() = Cov
= Cov![]() (Symmetry)
(Symmetry)
C2. Cov![]() .
.
C3. Cov![]() .
.
C4. Cov![]() .
.
Proof
C1.
![]()
C2.
![]()
C3.
![]()
C4.
![Rendered by QuickLaTeX.com \begin{align*} {\rm Cov}(X+Y,Z) &= {\rm E}\left[(X+Y)Z\right] - {\rm E}(X+Y){\rm E}(Z)\\ &= {\rm E}(XZ+YZ) - \left[{\rm E}(X)+{\rm E}(Y)\right]{\rm E}(Z)\\ &= {\rm E}(XZ) - {\rm E}(X){\rm E}(Z) + {\rm E}(YZ) - {\rm E}(Y){\rm E}(Z)\\ &= {\rm Cov}(X,Z) + {\rm Cov}(Y,Z). \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-343006bec65c9eb983978b918705997a_l3.png)
The last result in C4 can be extended in the obvious way. For example,
![]()
One can also represent this calculation in tabular form, as below.
| Cov(X,2X) = 2 Var(X) | Cov(X,3Y) = 3Cov(X,Y) | |
| Cov(2Z,2X) = 4Cov(X,Z) | Cov(2Z,3Y) = 6Cov(Y,Z) |
Example 6.6
Simplify ![]() .
.
Solution
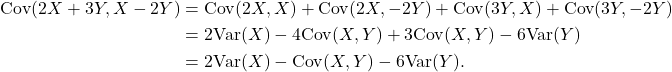
6.4 Sums of Random Variables ◊
|
MAIN RESULTS
|
Proof
-
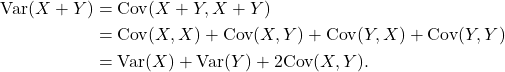
Similarly,
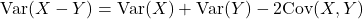 .
. - Exercise. Similar to 1.
- If
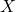 and
and 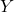 are independent then
are independent then 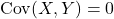 , so from
, so from  above it follows that
above it follows that
![Rendered by QuickLaTeX.com \[{\rm Var}(X \pm Y) = {\rm Var}(X) + {\rm Var}(Y).\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-3396c74314487214424b47e431b718e9_l3.png)
Extension of 3.
| If |
Example 6.7
The following table gives the joint pmf of the number (in hundreds) of single cones and double cones sold in an ice cream palour per day, the random variable ![]() denotes the number of single cones and
denotes the number of single cones and ![]() denotes the number of double cones sold per day.
denotes the number of double cones sold per day.
(a) Calculate the variance of
(i) total number, and (ii) the difference in the numbers of cones sold per day.
(b) The net profit on a single cone is $2 while that on a double cone is $3. What is the mean and variance of the total net profit in a day.
| 4 | 5 | 6 | |||
|---|---|---|---|---|---|
| 3 | 0.15 | 0.05 | 0 | 0.2 | |
| 4 | 0.05 | 0.25 | 0.1 | 0.4 | |
| 5 | 0 | 0.05 | 0.35 | 0.4 | |
| 0.2 | 0.35 | 0.45 | 1 | ||
Solution
The marginal distributions of ![]() and
and ![]() are given in the table. Calculations give
are given in the table. Calculations give
![]()
![]()
(a)(i) Let ![]() denote the total number of cones sold per day, so
denote the total number of cones sold per day, so ![]() . Then
. Then
![]()
that is, ![]() . Note that since the number of cones are in hundreds, the variance needs to be multiplied by
. Note that since the number of cones are in hundreds, the variance needs to be multiplied by ![]() .
.
(ii) Let ![]() denote the difference in the number of cones sold per day, so
denote the difference in the number of cones sold per day, so ![]() . Then
. Then
![]()
that is, ![]() .
.
(b) The net profit per day is ![]() . Then
. Then
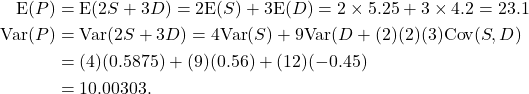
Thus the mean profit is $23,100 per day with a variance of ![]() , or a standard deviation of $316.28.
, or a standard deviation of $316.28.
6.5 Correlation coefficient
We saw in 6.3 that covariance is a measure of relationship between two random variables. The problem with covariance is that it is scale dependent, since
![]()
Thus, if we ![]() is height in metres and
is height in metres and ![]() is weight in kg, and
is weight in kg, and ![]() is height in cm and
is height in cm and ![]() is weight in g, then
is weight in g, then
![]()
But we are still measuring a relationship between the same quantities!
For this reason, the correlation coefficient if preferred as a measure of relationship between variable. We define the correlation coefficient as
![]()
It can be shown that ![]() .
.
Exercise
- Prove that correlation is scale independent, that is,
![Rendered by QuickLaTeX.com \[{\mid\rm Corr}(aX+b,cY+d)\mid = \mid{\rm Corr}(X,Y)\mid.\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-6de4677854754c4850c60a91c7ca917f_l3.png)
- For Example 6.7, calculate the correlation coefficient between the number of double and single cones sold per day.

