4 Random Variables
Learning Outcomes
At the end of this chapter you should be able to:
- explain the concept of a random variable;
- identify random variables as discrete or continuous;
- work with probability mass functions and cumulative distribution functions;
- compute expectations and variances and know their properties;
- understand the concepts of binomial distribution;
- understand the concepts of Poisson distribution;
- model and solve problems using random variables;
- conduct hypothesis tests for binomial proportion and Poisson mean.
Contents
4.4 Cumulative distribution function
4.5 Expectation or mean of a random variable
4.1 Introduction
A random experiment or event is one for which the outcome is not known in advance. Examples are:
- Will the stock market crash in October?
- Will interest rates go up next month?
- Will there be another pandemic in the next decade?
- Will there be another extreme weather event in Australia this year?
For such experiments/events the outcomes can only be described in terms of probabilities.
Two problems
- The outcomes of random experiments are often not numerical.
- Toss a single coin once. Sample space is
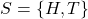 .
. - Interest rates:
- Toss a single coin once. Sample space is
This makes it difficult to apply the full power of mathematics to these situations.
- Several phenomena have common features.
- Toss a coin ten times. What is the probability of two heads?
- What is the probability that on two of the next ten days the Dow Jones index closes higher?
It is more efficient to study a generic model and then apply the results to all of them. This is called abstraction.
Solution
Translate outcomes from the sample space into numbers.
For the coin tossing example, the sample space is ![]() . Put
. Put
![Rendered by QuickLaTeX.com \[X = \begin{cases} 1, & \text{\ if H comes up}\\ 0, & \text{\ Otherwise} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-7084f45a1299c7fdd8756dc36eb179d8_l3.png)
Thus here ![]() counts the number of H obtained in one toss of a coin. The value
counts the number of H obtained in one toss of a coin. The value ![]() takes is random — it depends on the chance. We call
takes is random — it depends on the chance. We call ![]() a random variable.
a random variable.
Random Variable
A random variable (rv) is a function (mapping) from a sample space to the real numbers.
Example 4.1
Toss a coin twice. The sample space is ![]() . Let the random variable
. Let the random variable ![]() denote the number of H tossed. Then
denote the number of H tossed. Then
![Rendered by QuickLaTeX.com \[X = \begin{cases} 0, & \text{\ if TT comes up}\\ 1, & \text{\ if HT or TH comes up}\\ 2, & \text{\ if HH comes up} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-1c97273965851d64249336f1691098e5_l3.png)
Exercise
Let the rv ![]() correspond to the event at least one H is tossed when a coin is tossed twice. What values can
correspond to the event at least one H is tossed when a coin is tossed twice. What values can ![]() take, and which events in the sample space do they correspond to?
take, and which events in the sample space do they correspond to?
4.2 Discrete random variables
A random variable is discrete if its set of possible values can be listed. More formally, a random variable is discrete if its sample space is (finitely or infinitely) countable. Otherwise it is continuous.
In Example 5.1 above, ![]() is a discrete random variable.
is a discrete random variable.
Discrete random variables usually arise from counting processes (the number of: employees with degrees; breakdowns; insurance claims; faulty laptops). In contrast, continuous random variables usually arise from measurements (returns from a diversified assets portfolio, equipment lifetime, weight of a bag of flour labelled 1 kg).
Continuous random variables will be covered in Chapter 6.
Random variables and Data
Discrete data (usually) arises from observation on discrete random variables. Continuous data (usually) arises from observation on continuous random variables.
4.3 Probability mass function
The probability mass function (pmf) gives probabilities for discrete random variables. The pmf comes from the sample space.
For the single toss of a fair coin, let
![Rendered by QuickLaTeX.com \[X = \begin{cases} 1, & \text{\ if H comes up}\\ 0, & \text{\ otherwise.} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-f189aa497cf3d92e5932fe7282f06247_l3.png)
Then
![]()
This can be tabulated.
| 0 | 1 | |
|---|---|---|
| 0.5 | 0.5 |
![]()
![]() is called the pmf of
is called the pmf of ![]() . Sometimes
. Sometimes ![]() can be given by a formula. In other cases we can only give
can be given by a formula. In other cases we can only give ![]() as a table.
as a table.
Note on Notation
We use upper case letters from the end of the alphabet (such as ![]() ) to represent random variables, and the corresponding lower case letter (
) to represent random variables, and the corresponding lower case letter (![]() ) to represent a possible value of the rv.
) to represent a possible value of the rv.
Properties of pmfs
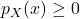 for all possible values of
for all possible values of 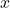 . Compare this with axiom P2 for probabilities.
. Compare this with axiom P2 for probabilities.-
![Rendered by QuickLaTeX.com \[\sum_x p_X(x) = 1,\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-c56a638c3a5d4988dbd8280033791205_l3.png)
where the sum is over all the possible values of
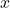 . Compare with with axiom P1 for probabilities.
. Compare with with axiom P1 for probabilities.
These properties follow from the properties of probabilities.
Example 4.2
The number of passengers for a scenic helicopter flight varies at random from none to a maximum of four. Passengers can either make a booking or simply turn up. The probability mass function for the rv ![]() which denotes the number of passengers is given below.
which denotes the number of passengers is given below.
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0.1 | 0.4 | 0.1 | 0.1 |
(a) Determine the value of ![]() .
.
(b) What is the probability that fewer than three passengers are on a flight?
(c) What is the probability that a flight has fewer than three passengers if there is a booking for only one passenger? Assume that booked passengers always turn up.
Solution
(a) Since the probabilities sum to 1, ![]() .
.
(b) ![]() .
.
(c) Here we know there is at least one passenger. So we want
![]()
Note
- AND is equivalent to intersection
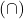 .
. - OR is equivalent to union
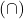 .
. - IF is equivalent to conditional.
Defining events
Put ![]() . These are events. Part (c) asks for
. These are events. Part (c) asks for
![]()
ALL the rules of probability still hold:
![]()
Further, the theorem of Total Probabilities holds:
![]()
as does complements:
![]()
4.4 Cumulative distribution function
The cumulative distribution function of a random variable ![]() at
at ![]() , denoted
, denoted ![]() , is defined as
, is defined as
![]()
For a discrete random variable,
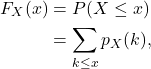
that is, the sum of probabilities for all values less than and including ![]() .
.
Example 4.3
| -1 | 0 | 1 | 2 | |
|---|---|---|---|---|
| 0.2 | 0.1 | 0.4 | 0.3 | |
| 0.2 | 0.3 | 0.7 | 1.0 |
Using the cumulative distribution function,
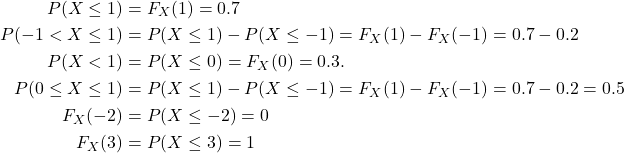
Some properties of CDFs
- By properties of probabilities, it follows that
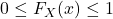 .
. - In general,
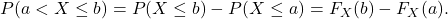 Note that this includes the probability of
Note that this includes the probability of 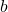 but not of
but not of  .
. - The cdf and pmf contain the same information but in different forms, and one can be obtained from the other.
Graph of the CDF
The graph of the cdf from Example 4.3 is given below. The cdf and pdf can both be obtained from the graph of the cdf.
Note that the graph is closed at the end-points indicated by full circles, and open at the other end-points. Thus ![]() , but just below -1 the cdf is 0.
, but just below -1 the cdf is 0.
4.5 Expectation
Consider the following data:
![]()
We want to calculate the mean of this data. We can obtain the frequency distribution of the data, as given in the table below.
| 1 | 1 | 3 | 3 |
|---|---|---|---|
| 2 | 2 | 2 | 4 |
| 3 | 3 | 2 | 6 |
| 4 | 4 | 2 | 8 |
| 5 | 5 | 1 | 5 |
The mean is calculated as
![]()
It can also be calculated by the grouped frequency data, as
![]()
In general for a data set with ![]() distinct values
distinct values ![]() each with corresponding frequency
each with corresponding frequency ![]() ,
, ![]() , the mean is
, the mean is
![]()
Let ![]() . Now since the sum of the frequencies in the denominator is a constant, we can divide this into the sum in the numerator, giving
. Now since the sum of the frequencies in the denominator is a constant, we can divide this into the sum in the numerator, giving
![]()
The term ![]() is the relative frequency for data point
is the relative frequency for data point ![]() . Note that
. Note that
![]()
That is, to compute the mean of the data we multiply the data values with the corresponding relative frequency and sum these values. Note that the relative frequencies have similar properties to probabilities. They are non-negative and sum to 1. In fact relative frequencies are the observed probability for each data point.
We use this idea to define the mean of a random variable.
Definition: Expected value
![]()
Expected value of a function of a random variable
![]()
![]()
Example 4.4
Toss a fair coin once and let the rv ![]() denote the number of heads tossed. The pmf of
denote the number of heads tossed. The pmf of ![]() is given below.
is given below.
| X | 0 | 1 |
|---|---|---|
| p_X(x) | 0.5 | 0.5 |
Then
![]()
This is a long run average, so that in a large number of trials of tossing the coin we would expect half of them to be heads.
Example 4.5
| X | -1 | 0 | 1 | 2 |
|---|---|---|---|---|
| p_X(x) | 0.1 | 0.2 | 0.3 | 0.4 |
Calculate ![]() ,
, ![]() and
and ![]() .
.
Solution
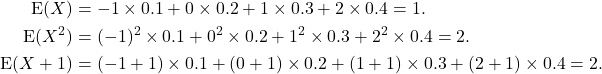
Note that ![]() .
.
Notes
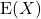 is also called the expectation or the mean of
is also called the expectation or the mean of 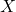 .
.- We also use the symbol
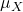 for
for 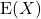 . (
. (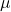 is the Greek letter mu.)
is the Greek letter mu.) - In general,
![Rendered by QuickLaTeX.com {\rm E}\left(X^2\right) \ne \left[{\rm E}\left(X\right)\right]^2](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-b60508440f35775c539f941235c0e421_l3.png) .
.
Properties of expectation
E1. For any constant ![]() ,
, ![]() .
.
E2. For constants ![]() and
and ![]() ,
, ![]() .
.
E3. For random variables ![]() and
and ![]() ,
, ![]() .
.
E4. ![]() .
.
The last result is similar to ![]() .
.
Proof
E1. A random variable that is constant with value ![]() takes only the value
takes only the value ![]() with probability
with probability ![]() .
.
| 1 |
Then
![]()
E2. We use properties of summations for this proof.
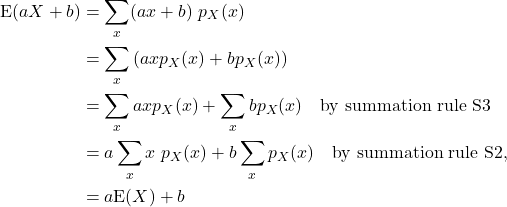
where in the last line we have used the fact that ![]() .
.
E3. This proof requires the properties of joint distributions, so we will omit it.
E4. First we note that ![]() is a constant (that is, its expectation is itself:
is a constant (that is, its expectation is itself: ![]() ).
).
![]()
4.6 Variance
For a random variable ![]() , we define the variance of
, we define the variance of ![]() , denoted
, denoted ![]() , by
, by
![]()
Compare with the definition of the variance for data:
![]()
which is an “average” of ![]() .
.
We also write ![]() for Var
for Var![]() .
.
The standard deviation of ![]() , denoted
, denoted ![]() , is the positive square root of variance, that is,
, is the positive square root of variance, that is,
![]()
Example 4.6
| X | -1 | 0 | 1 | 2 |
|---|---|---|---|---|
| p_X(x) | 0.1 | 0.2 | 0.3 | 0.4 |
From Example 4.5,
![]() , so
, so
![Rendered by QuickLaTeX.com \begin{align*} {\rm Var}(X) &= {\rm E}\left[\left(X-\mu_X\right)^2\right]\\ &= (-1-1)^2(0.1) + (0-1)^2(0.2) +(1-1)^2(0.3) +(2-1)^2(0.4)\\ &= 1. \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-86ec1254c3a682fc437060228500559a_l3.png)
Properties of variance
V1. Var![]() .
.
V2. Var![]() . This form is simpler for calculating variance.
. This form is simpler for calculating variance.
(Compare with ![]() .)
.)
V3. Var![]() .
.
(Compare with ![]() .)
.)
Proof
V1.
![Rendered by QuickLaTeX.com \[{\rm Var}(X) = {\rm E}\left[\left(X-\mu_X\right)^2\right] = \sum_x \underbrace{\left(x-\mu_X\right)^2}_{\ge 0}\ \underbrace{p_X(x)}_{\ge 0} \ge 0,\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-bfc72a0ce98878fa6aebdfe647cbe8f3_l3.png)
as each term in the sum is non-negative ![]() .
.
V2.
![Rendered by QuickLaTeX.com \begin{align*} {\rm Var}(X) &= {\rm E}\left[\left(X-\mu_X\right)^2\right]\\ &= {\rm E}\left[\left(X-\mu_X\right)\left(X-\mu_X\right)\right]\\ &= {\rm E}\left[X(X-\mu_X) - \mu_X(X-\mu_X)\right]\\ &= {\rm E}\left[X^2-\mu_X\ X\right] - \mu_X\underbrace{{\rm E}(X-\mu_X)}_{=0}\\ &= {\rm E}\left(X^2\right) - \mu_X {\rm E}(X)\\ &= {\rm E}\left(X^2\right) - \mu_X^2 = {\rm E}\left(X^2\right) -\left( {\rm E}(X)\right)^2. \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-27c6728e27b3cc3b6564e5cd56c36c4a_l3.png)
V3.
![Rendered by QuickLaTeX.com \begin{align*} {\rm Var}(aX+b) &= {\rm E}\left[\left(aX+b-{\rm E}\left(aX+b\right)\right)^2\right]\\ &= {\rm E}\left[\left(aX+b-a{\rm E}(X)-b\right)^2\right]\\ &= {\rm E}\left(\left[a(X-\mu_X)\right]^2\right)\\ &= {\rm E}\left[a^2(X-\mu_X)^2\right]\\ &= a^2\ {\rm E}\left[\left(X-\mu_X\right)^2\right]\\ &= a^2\ {\rm Var}(X). \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-2c32252f31e48270b24ae1d942c7f16f_l3.png)
Note that the standard deviation of ![]() , denoted
, denoted ![]() , is given by
, is given by ![]() .
.
Example 4.7
A builder is under contract to complete a project in no more than three months or there will be heavy cost overruns. Given the timings of scheduled work, the manager of the construction believes that the job can be finished in either 2, 2.5, 3 or 3.5 months, with
corresponding probabilities 0.1, 0.2, 0.4 and 0.3. Find the expected completion time and the variance, and interpret these quantities.
Solution
Step 1 Define an appropriate random variable.
Let the random variable ![]() denote the time to complete the project.
denote the time to complete the project.
Step 2 Determine its distribution.
| 2 | 2.5 | 3 | 3.5 | |
|---|---|---|---|---|
| 0.1 | 0.2 | 0.4 | 0.3 |
![Rendered by QuickLaTeX.com \begin{align*} {\rm E}(X) &= 2\times 0.1 + 2.5\times 0.2 + 3\times 0.4 + 3.5\times 0.3 = 2.95 {\rm \ months}\\ {\rm E}(X^2) &= 2^2\times 0.1 + 2.5^2\times 0.2 + 3^2\times 0.4 + 3.5^2\times 0.3 = 8.925\\ {\rm Var}(X) &= {\rm E}(X^2) - \left[{\rm E}(X)\right]^2 = 8.925 - 2.95^2 = 0.2225.\\ \sigma_X &= \sqrt{0.2225} = 0.4717 {\rm\ months} \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-0c58cb1bfee2167ab4d7b3616614f066_l3.png)
The mean time to completion is 2.95 months, with a standard deviation of 0.47 months. In addition, the probability of the construction time exceeding 3 months is 0.3, which is quite large. From this we conclude that it is very likely that the construction time will exceed 3 months.
Example 4.8
A square window frame produced by a machine has sides with mean length 2.5 m and variance 0.1 m![]() . (Assume that the sides of each window are exactly equal.)
. (Assume that the sides of each window are exactly equal.)
(a) Find the mean and variance of the perimeter of the frames.
(b) What is the mean area of the frames?
Solution
Let the random variable ![]() denote the length of a side of the window. Then
denote the length of a side of the window. Then ![]() and
and ![]() .
.
(a) Let the random variable ![]() denote the perimeter of the window. Then
denote the perimeter of the window. Then ![]() , so
, so
![]()
(b) Let the random variable ![]() denote the area of the window. Then
denote the area of the window. Then ![]() . Now
. Now
![Rendered by QuickLaTeX.com \begin{align*} {\rm Var}(X) &= {\rm E}(X^2) - \left[{\rm E}(X)\right]^2\\ \Rightarrow {\rm E}(A) &= {\rm E}(X^2) = {\rm Var}(X) + \left[{\rm E}(X)\right]^2 = 0.1 + 2.5^2 = 6.35 {\rm m}^2. \end{align*}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-8474c75b6a80927f5f486d079bd699bc_l3.png)
Standardised random variable
Let the random variable ![]() have mean
have mean ![]() and standard deviation
and standard deviation ![]() . Put
. Put
![Rendered by QuickLaTeX.com \[Z= \frac{X-\mu_X}{\sigma_X} = \underbrace{\frac{1}{\sigma_X}}_{a}\ X - \underbrace{\frac{\mu_X}{\sigma_X}}_{b}.\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-89a0c66e76bd267cd614a2650724667f_l3.png)
Then
![]()
![]()
We call ![]() a standardised random variable. This result is similar to that for standardising data (see Section 3.8 in Chapter 3):
a standardised random variable. This result is similar to that for standardising data (see Section 3.8 in Chapter 3):
![]()
Note
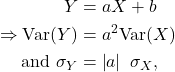
since standard deviation is always non-negative. This is similar to the result for
linear transformation of data. Note that
![Rendered by QuickLaTeX.com \[\left |a\right| = \begin{cases} a {\rm \ if\ } a \ge 0,\\ -a {\rm \ if\ } a < 0. \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-b2dd4f833dfd96d1fd8474a7a2e8e618_l3.png)
Risk in investment
In investments, one measure of risk is the standard deviation of the return. So if two investments have similar mean returns, the one with the larger standard deviation has larger risk. Usually the investment with larger mean return has larger risk (standard deviation).
4.7 Bernoulli distribution
The random variable ![]() has a Bernoulli disttibution if it takes only two values,
has a Bernoulli disttibution if it takes only two values, ![]() and
and ![]() , with
, with ![]() and
and ![]() ,
, ![]() . We write
. We write ![]() . (The symbol
. (The symbol ![]() is read “is distributed as”, or “ has the distribution”.)
is read “is distributed as”, or “ has the distribution”.)
The pmf of the ![]() is given below, and from this the mean and variance of
is given below, and from this the mean and variance of ![]() can be found.
can be found.
| 0 | 1 | |
|---|---|---|
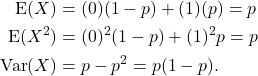
|
|
Example 4.9
(a) Toss a fair coin once, and let the rv ![]() denote the number of H. Then
denote the number of H. Then ![]() .
.
(b) Toss a fair die once and let the rv ![]() denote the number of fives or sixes tossed. Then
denote the number of fives or sixes tossed. Then ![]() .
.
(c) In the current economic environment the probability that the RBA will raise interest rates next month is estimated as ![]() . Let the rv
. Let the rv ![]() take the value
take the value ![]() if the interest rate goes up and
if the interest rate goes up and ![]() otherwise. Then
otherwise. Then ![]() . The mean and variance of
. The mean and variance of ![]() are
are
![]()
4.8 Binomial distribution
Toss a fair coin ten times. What is the probability of obtaining five heads? This example encapsulates the following key features, that are common in many situations.
- A fixed number
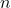 of independent and identical trials.
of independent and identical trials. - Each trial has exactly two possible outcomes, denoted success (S) and failure (F).
- The probability of success is
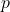 which is fixed throughout the trials.
which is fixed throughout the trials. - Let the rv
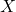 denote the number of successes in these trials.
denote the number of successes in these trials.
Then ![]() has a binomial distribution with parameters
has a binomial distribution with parameters ![]() and
and ![]() . We write
. We write ![]() .
.
Note that in this notation, ![]() .
.
Probabilities for Bin(n,p)
The probability that stock market falls on any given day is 0.3. Assume that the market falls or rises independently of the previous day’s performance. What is the probability that in a week of six trading days, the market will fall in two of them?
We can list the sample space here. Let F denote that the market falls and N that it does not. Then the sample space is
NNNNNN, FNNNNN, NFNNNN, NNFNNN, NNNFNN, NNNNFN, NNNNNF, FFNNNN, FNFNNN, FNNFNN, …
Now by independence,
![]()
Observations
- The two Falls can occur on any two of the six days.
- The probability of any of the sequences containing two Falls is the same, that is,
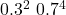 .
. - If we can COUNT the number of ways of getting two falls out of six, then we can find the probability of two Falls in six days by multiplying this number with the probability
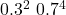 .
.
COUNTING TECHNIQUES — Combinatorics
In effect in the above example we need to select the two places that falls can occur out of six. In general, the number of ways of selecting ![]() things out of
things out of ![]() is given by
is given by
![]()
where
![]()
For this notation to make sense, we define ![]() . For example,
. For example,
![Rendered by QuickLaTeX.com \[\dbinom{n}{n}=\frac{n!}{n!\underbrace{(n-n)!}_{=0!=1}} = 1, \dbinom{n}{1} = \frac{n!}{1!(n-1)!}=\frac{n(n-1)!}{1!(n-1)!} = n,\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-71f67008541544376cecfdd6243bd73b_l3.png)
![Rendered by QuickLaTeX.com \[\dbinom{6}{2} = \frac{6!}{\underbrace{2!4!}_{Add\ to\ 6}} = \frac{6.5.4!}{2!4!} = 15, \dbinom{10}{2}=\frac{10!}{2!8!} = \frac{10.9.8!}{\underbrace{2!8!}_{Add\ to\ 10}} = 45.\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-1f61ce8a31eb1b94c3d87c8f6613b456_l3.png)
Example 4.10
(a) In how many ways can two stocks be selected for purchase out of 10?
(b) A part-time worker works only two day a week. In how many possible ways can he select his weekly roster? Assume a five day week.
(c) On a two day trip to Singapore, I want to stay in a different hotel each day. There are six hotels in the locality I want to stay in. How many ways different choices of hotel combinations do I have?
Solution
(a)
![]()
(b)
![]()
(c)
![]()
Note
On most calculators you can quickly compute combinations using the button
![]()
We can also perform this calculation in R, as below.
choose(10,2)
[1] 45
choose(5,2)
[1] 10
choose(6,2)
[1] 15
Probabilities for 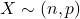
First note that ![]() for
for ![]() and
and ![]() . Next,
. Next, ![]() for
for ![]() indicates that there are
indicates that there are ![]() successes and the remaining
successes and the remaining ![]() trials are failures. Thus the probability mass function for
trials are failures. Thus the probability mass function for ![]() is
is
![]()
where
-
![Rendered by QuickLaTeX.com \[\begin{pmatrix}n\\ r \end{pmatrix} = \frac{n!}{r!\left(n-r\right)!}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-d09e4ce3f713d0ad6391d7e23bbb8ffe_l3.png)
is the number of ways of obtaining
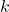 successes from
successes from 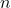 trials;
trials; 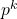 is the probability of the
is the probability of the 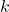 successes;
successes;-
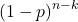 is the probability of the
is the probability of the 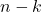 failures.
failures.
The cumulative distribution function
The cdf for ![]() is
is
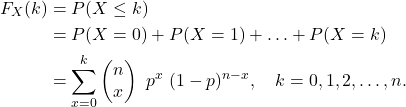
Note
Probabilities for the binomial distribution can be obtained:
- using the formula — this will be used for a few examples only;
- using tables — tables are available only for certain values of
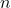 and
and 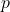 ;
; - using software such as R — this will be our preferred method.
Example 4.11
The probability that stock the market falls on any given day is 0.3. Assume that the market falls or rises independently of the previous day’s performance. What is the probability that in a week of six trading days,
(a) the market fall in two of them?
(b) the market falls on at least one day?
Solution
Let the rv ![]() denote the number of days that the market falls out of six. Then
denote the number of days that the market falls out of six. Then ![]()
(a)
![]()
Using R,
dbinom(2,6,0.3)
[1] 0.324135
(b) Now we need
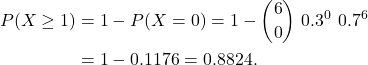
Again, using R,
pbinom(0,6,0.3, lower.tail = F)
[1] 0.882351
Note that by default pbinom() gives the lower tail probability, that is, ![]() . The option lower.tail = F gives the corresponding upper tail probability, that is,
. The option lower.tail = F gives the corresponding upper tail probability, that is, ![]() . These are illustrated with the code below.
. These are illustrated with the code below.
> pbinom(0,6,0.3) [1] 0.117649 > 1 - pbinom(0,6,0.3) [1] 0.882351 > pbinom(0,6,0.3, lower.tail = F) [1] 0.882351
A note on R
In R, the base function for the binomial distribution is binom. This can be used in three ways determined by the letter used before it. So dbinom(k, n, p) give ![]() for
for ![]() distribution. Similarly, pbinom(k,n,p) gives
distribution. Similarly, pbinom(k,n,p) gives ![]() , and rbinom(k, n, p) gives a simulation of
, and rbinom(k, n, p) gives a simulation of ![]() random values from a
random values from a ![]() distribution.
distribution.
We will see a similar syntax for other probability distributions.
Example 4.12
Fiddler crabs are tiny semi-terrestrial marine crabs found in mangrove swamps in the tropical belt.

Image by Richard Alexander from Pixabay
An ecologist is studying the roaming behaviour of fiddler crabs. He identifies 20 burrows that are occupied by fiddler crabs. Every afternoon he checks the burrows for presence of the crabs. The probability that a crab is in its burrow is ![]() . Assume that the crabs are present independently of each other. What is the probability that the number of burrows with a crab is
. Assume that the crabs are present independently of each other. What is the probability that the number of burrows with a crab is
(a) zero,
(b) exactly ![]() ,
,
(c) at least ![]() ,
,
(d) at most 5.
Solution
Let the rv ![]() denote the number of burrows out of
denote the number of burrows out of ![]() that have a crab. Then
that have a crab. Then ![]() .
.
(a) ![]() .
.
(b) ![]() .
.
(c) ![]() using R,
using R,
pbinom(9,20,0.2, lower.tail = F)
[1] 0.002594827
(d) ![]() , using R,
, using R,
pbinom(5,20,0.2)
[1] 0.8042078
MEAN AND VARIANCE OF 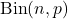
|
|
Proof
For the proof we express the binomial distribution as a sum of ![]() individual
individual ![]() trials. Let the rv
trials. Let the rv ![]() denote the number of successes in
denote the number of successes in ![]() independent and identical Bernoulli trials, and let
independent and identical Bernoulli trials, and let ![]() represent the number of successes in the individual trials. Then for
represent the number of successes in the individual trials. Then for ![]() ,
,
![Rendered by QuickLaTeX.com \[Y_i=\begin{cases} 1, \text{\ if trial $i$ is a success}\\ 0, \text{\ otherwise.} \end{cases}\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-fede4b4886e8f5f0eea2d8043d3a3d8d_l3.png)
Now ![]() , are independent, and
, are independent, and ![]() . Further,
. Further,
![]()
so
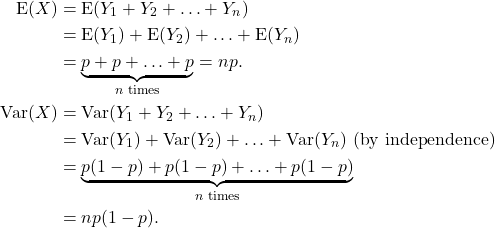
Note that we have used the result that the variance of a sum of independent random variables is the sum of the variances, proved in Chapter 6.
Example 4.13
A farmer plants mango trees in clusters of 20 per 100 square metres. Each tree in a cluster will produce fruit this year with probability 0.6. The farmer has 5 such clusters.
(a) What is the probability that in a cluster more than 15 trees will produce fruit this year?
(b) What is probability that in at least one cluster more than 15 trees will produce fruit this year?
(c) What is the expected total number of trees that will produce fruit this year?
(d) What assumption(s) have you made in your solution?
Solution
(a) Let the rv ![]() denote the number of trees in a cluster this year that produce fruit. Then
denote the number of trees in a cluster this year that produce fruit. Then ![]() , so
, so
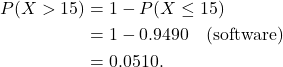
(b) Let the rv ![]() denote the number of clusters in which more than
denote the number of clusters in which more than ![]() trees produce fruit. The
trees produce fruit. The ![]() , and
, and
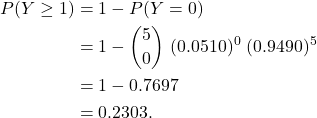
(c) We can approach this problem in two ways.
Let ![]() be the number of trees that fruit in cluster
be the number of trees that fruit in cluster ![]() ,
, ![]() . Then
. Then ![]() , so
, so ![]() . Now put
. Now put ![]() , denote the total number of trees that fruit. Then
, denote the total number of trees that fruit. Then
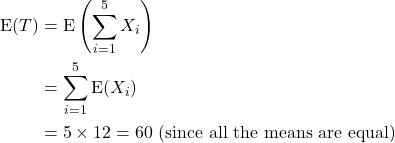
Alternatively, we can consider the number of trees that fruit as a set of 20 Bernoulli trials for each cluster, giving a total of 100 trials. The the number of trees that fruit is ![]() , so
, so ![]() as before.
as before.
(d) we have assumed that each tree in a cluster fruits independently of other trees, and also the fruiting between trees in different cluster is also independent. We have also assumed that the probability of a tree fruiting is fixed at 0.6. The independence assumption may not hold, as the fruiting of trees in a cluster are most likely dependent.
4.9 Poisson distribution
The Poisson distribution models the number of occurrences of a phenomenon in a fixed interval or fixed time period or fixed area or fixed volume. Here volume is a generic term and can be interpreted as any fixed unit. This is a counting process, similar to the binomial distribution.
Examples are:
- The number of stars in a region (volume) of the galaxy.
- The number of aphids on a leaf of a rose bush.
- The number of arrivals per minute at a toll bridge.
- The number of times a printer breaks down in a month.
- The number of paint spots on a new car.
- The number of sewing flaws per pair of jeans during production.
- The number of eggs laid by an ostrich in a season.
Assumptions of the Poisson distribution
- The occurrences are independent of each other.
- Two occurrences cannot happen at the same location.
- The mean number of occurrences in a specified volume is fixed.
Comparison with Bin(n,p)
- Binomial distribution has a fixed number of trials. Poisson does not.
- Binomial distribution has two parameters,
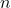 and
and 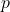 . Poisson has only one: the mean number of occurrences.
. Poisson has only one: the mean number of occurrences. - Binomial has two possible outcomes, Success and Failure, at each trial. Poisson does not.
- Binomial random variable takes the values
 . Poisson takes values 0,1,2, ….
. Poisson takes values 0,1,2, ….
Probability mass function
Let the random variable ![]() have a Poisson distribution with parameter
have a Poisson distribution with parameter ![]() , the mean number of occurrences in a fixed volume. We write
, the mean number of occurrences in a fixed volume. We write ![]() . Then
. Then
![]()
The cumulative distribution function of ![]() is given by
is given by
![Rendered by QuickLaTeX.com \[P(X \le k) = F_X(k) = \sum_{x=0}^k \frac{e^{-\lambda}\ \lambda^x}{x!}, \quad k=0,1,2,\ldots\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-0c3fb8508f074977784eb0c22af70ed3_l3.png)
that is, simply add up the probabilities up to and including ![]() .
.
Exercise
Do the probabilities add up to 1?
Example 4.14
Poole studied 41 African male elephants in Amboseli National Park in Kenya for a period of 8 years and recorded the age of each elephant and the number of successful matings. (Poole, J. (1989). ‘Mate Guarding, Reproductive Success and Female Choice in African Elephants’. Animal Behavior (37): 842–849.) The mean number of successful mating in 8 years was 2.7.
(a) What is the probability of exactly 2 successful mating in eight years by an adult male elephant?
(b) What is the probability of no successful mating in eight years by an adult male elephant?
(c) What is the probability of at least 5 successful matings in eight years by an adult male elephant?
(d) What is the probability of more than 5 successful matings in eight years by an adult male elephant?
(e) What is the probability of exactly 2 successful matings in 16 years by an adult male elephant?
Solution
Let the rv ![]() denote the number of successful mating in 8 years by an adult male elephant. Then
denote the number of successful mating in 8 years by an adult male elephant. Then ![]() .
.
(a)
![]()
Using R, the base function is pois(). For the individual probability for this part,
dpois(2, 2.7)
[1] 0.2449641
(b)
![]()
Using R,
dpois(0, 2.7)
[1] 0.06720551
(c)
![]()
using R,
ppois(4,2.7, lower.tail = F)
[1] 0.1370921
(d)
![]()
using R,
ppois(5,2.7, lower.tail = F)
[1] 0.05673167
(e) Let the random variable ![]() denote the number of successful mating in 16 years by an adult male elephant. Now the time interval has doubled, so the mean number of successful matings in 16 years is
denote the number of successful mating in 16 years by an adult male elephant. Now the time interval has doubled, so the mean number of successful matings in 16 years is ![]() . Then
. Then ![]() .
.
![]()
Using R,
dpois(5, 5.4)
[1] 0.1728213
MEAN AND VARIANCE OF Poi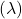 .
.
|
4.10 Hypothesis test for Binomial Proportion
Consider the following scenarios.
- The probability a fiddler crab is in its burrow at sunset is 0.6 in summer. An ecologist believes this proportion is higher in winter. She examines 20 burrows at sunset in July in Queensland and finds 14 crabs. Is the probability that a fiddler crab is in its burrow at sunset higher in winter?
- A marketing campaign was launched with the aim of increasing market share for Coles Supermarket, which currently stands at 60%. A survey of 1000 randomly selected shoppers found that 650 of them shopped at Coles. Has the market share of Coles increased?
Note that the survey gives the market share of Coles as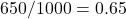 , or 65%.
, or 65%. - The probability of a still birth in the general population is 0.01. A medical researcher believes that this rate is higher in the migrant population. Data over a month shows that out of a total of 1,000 pregnancies in migrant women, 15 resulted in still births. Is the proportion of still births higher in the migrant population?
Observations
- All the above questions deal with assessing a binomial probability based on data. This falls under the topic of inference.
- The method commonly used for this particular type of problem depends on the sample size, that is, the number of observations or the number of units or the value of
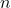 .
.
We will illustrate the ideas below using the simple coin tossing problem: A coin is tossed 20 times and results in 13 heads. Is the coin biased in favour of head?
Let the random variable ![]() denote the number of heads obtained in
denote the number of heads obtained in ![]() tosses of the coin. Then
tosses of the coin. Then ![]() . This is the test statistic, that is, we will use the value of this random variable to test the hypotheses of interest. Here the value of
. This is the test statistic, that is, we will use the value of this random variable to test the hypotheses of interest. Here the value of ![]() is not known, and we want to make a decision regarding its value.
is not known, and we want to make a decision regarding its value.
Note that the binomial distribution has two parameters: ![]() and
and ![]() . Here the value of
. Here the value of ![]() is known, and the inference deals with the value of the parameter
is known, and the inference deals with the value of the parameter ![]() .
.
| Inference ALWAYS deals with a population parameter. |
Steps
- State the hypotheses to be tested. That is, state what the current belief/value is for the binomial probability, and the belief or change expected. Null Hypothesis: the current belief, or belief of no change. In the coin tossing example, we begin by believing that the coin is fair. (If we believe the coin is biased in favour of heads, we need to know the bias, that is, what is the probability of tossing a H?)
![Rendered by QuickLaTeX.com \[H_0: \text{Coin is fair, that is} \qquad H_0: p = 0.5\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-0efde8a2171a10dc9961e82fd4091966_l3.png)
- Alternative hypothesis: this is really the value of the parameter under the stated test: Is the coin biased in favour of heads? If the coin is biased in favour of heads, then what is value of
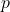 ?
?
![Rendered by QuickLaTeX.com \[\text{Coin is biased, that is} \qquad H_1: p > 0.5\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-4d2c7934a3c5f736c44bb7b47c99a919_l3.png)
- p-value: We need some way of assessing if the coin is fair based on our data. Here, the observed number of heads,
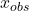 , is 13. We base our assessment on probabilities. What is the probability of obtaining
, is 13. We base our assessment on probabilities. What is the probability of obtaining 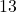 heads in
heads in 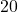 tosses if the coin is in fact fair? Under the null hypothesis, the distribution of the test statistic is Bin
tosses if the coin is in fact fair? Under the null hypothesis, the distribution of the test statistic is Bin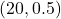 . This is called the null distribution. Then
. This is called the null distribution. Then
![Rendered by QuickLaTeX.com \[P(X=13\mid p=0.5) = 0.0739\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-263c605a0a1008fb7bbc8c7e7ec96f75_l3.png)
Note that
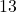 is the observed number of heads and
is the observed number of heads and 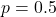 is the value of
is the value of 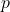 assumed under
assumed under 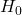 .
. - Is this probability large or small? Are we likely to get
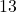 heads if the coin is really fair?
heads if the coin is really fair? - If we think that
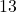 heads are too many for a fair coin, then any more than 13 will also be considered too many for a fair coin. So we should really be evaluating
heads are too many for a fair coin, then any more than 13 will also be considered too many for a fair coin. So we should really be evaluating 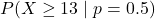 . We call this the p-value:
. We call this the p-value:
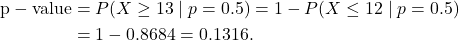
- Decision: if the p-value is small then the data is inconsistent with the null hypothesis. Then:
either the coin is not fair, that is, it is biased in favour of heads; or
we have unusual data, or a rare event. In hypothesis testing we ignore the occurrence of rare events. Thus we would conclude that the coin is biased in favour of heads if the p-value is considered to be small. - Significance level. If the p-value is less than the significance level, then it is deemed to be too small. The significance level is set in advance, before the hypothesis test is conducted. Usually the significance level is set at 2.5% (0.025) or 5% (0.05). Any event that occurs with probability less than
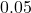 is taken to be infrequent or rare. In our example,
is taken to be infrequent or rare. In our example,
![Rendered by QuickLaTeX.com \[\text{p-value} = 0.1316 > 0.025.\]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-a15f3b62326e12e0ff39171f24a2725f_l3.png)
- Conclusion. Since p-value
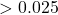 , there is insufficient evidence to reject the null hypothesis at the
, there is insufficient evidence to reject the null hypothesis at the 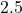 % level of significance. We conclude that there is insufficient evidence that the coin is biased.
% level of significance. We conclude that there is insufficient evidence that the coin is biased.
Writing Conclusions to Hypothesis tests
The conclusion must be written in terms of the question of interest in clear, simple terms. It must
- answer the question of interest,
- be unambiguous,
- impossible to misinterpret,
- in the language of the context/discipline/subject.
Note
The steps in Example 4.14 are for explaining the method. In practice we do not need to list them. The next example shows a more direct and simplified solution.
Example 4.15
A garden centre claims that only 10% of their mango seeds fail to germinate. A mango farm trials 20 mango seeds from the garden centre and finds that 4 of them do not germinate. Is the garden centre’s claim incorrect? Use a significance level of 0.025 (2.5%).
Solution
Let the random variable ![]() denote the number of seeds that do not germinate out of
denote the number of seeds that do not germinate out of ![]() .
.
Then ![]() , where
, where ![]() is the proportion of seeds that do not germinate.
is the proportion of seeds that do not germinate.
![]()
Note that the null hypothesis states the null belief, that the claim of the garden centre is true. The alternative hypothesis states the statement to be tested, that more than 10% of seeds do not germinate. The observed value of the test statistic is ![]() . The p-value of the test is
. The p-value of the test is
![]()
so the data provides insufficient evidence against the null hypothesis. We conclude on the basis of this analysis that there is no reason to doubt the garden centre’s claim.
Notes
- In the statements of the hypotheses, the null hypothesis always contains the equality value. Since the equality value is used to calculate the p-value, it is sufficient to state the null hypothesis as
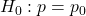 .
. - The alternative hypothesis never includes equality. So it will be stated as
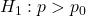 (upper-sided test) or
(upper-sided test) or 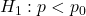 (lower-sided test) or
(lower-sided test) or 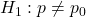 (two-sided test).
(two-sided test). - If a significance level is not specified then we use a 2.5% (0.025) for a one-sided test and 5% (0.05) for a two-sided test. The justification for this will be provided later.
- For a one-sided test, the probability expression for the p-value follows the same direction as the alternative hypothesis. Thus if
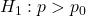 then p-value
then p-value 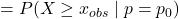 . Similarly, if
. Similarly, if 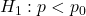 then p-value
then p-value 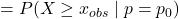 . We will see the examples of two-sided tests later.
. We will see the examples of two-sided tests later. - Usually one has an indication of the direction of change expected, so it is preferable to state a one-sided alternative hypothesis.
Example 4.16 A genetics example
Mouse genomes have 19 non-sex chromosome pairs, and X and Y sex chromosomes (females have two copies of X, males one each of X and Y). The total proportion of mouse genes on the X chromosome is 6.1%. 25 mouse genes are involved in sperm formation. An evolutionary theory states that these genes are more likely to occur on the X chromosome than elsewhere in the genome because recessive alleles that benefit males are acted on by natural selection more readily on the X than on autosomal (non-sex) chromosomes. On the other hand, the independence chance model would expect only 6.1% of the 25 genes to be on the X chromosome. In the mouse genome, 10 of 25 genes (40%) are on the X chromosome. Is the independence chance model appropriate for the mouse genome?
Solution
Let the random variable ![]() denote the number of genes, out of 25, on the X chromosome. Then
denote the number of genes, out of 25, on the X chromosome. Then ![]() , where
, where ![]() denotes the proportion of genes on the X chromosome. The hypotheses of interest are:
denotes the proportion of genes on the X chromosome. The hypotheses of interest are:
![]()
That is, we assume ![]() that the independence model holds, and the alternative hypothesis is in favour of the evolutionary hypothesis. The observed number of genes on the X chromosome is 10, so the p-value of the test is
that the independence model holds, and the alternative hypothesis is in favour of the evolutionary hypothesis. The observed number of genes on the X chromosome is 10, so the p-value of the test is
![]()
so there is overwhelming evidence against the null hypothesis. We conclude the independence chance model is not appropriate for the mouse genome, and the evolutionary model is more appropriate.
4.11 Hypothesis test for Poisson mean
The hypothesis test for the Poisson mean proceeds in the same manner as for binomial proportion. The only difference is that the p-value is calculated using the Poisson distribution. The example below illustrates the method.
Example 4.17 Hypothesis test for Poisson mean
Quality control requires the number of stitching flaws on a garment to be at most one on average. An inspection of a random sample of 3 garments gave a total of 6 flaws. Are the average numbers of flaws per garment as required? Use a significance level of 2.5%.
Solution
Let the random variable ![]() denote the number of stitching flaws in 3 garments. (This is our test statistic.) Let the average number of flaws in three garments be
denote the number of stitching flaws in 3 garments. (This is our test statistic.) Let the average number of flaws in three garments be ![]() . Then
. Then ![]() . Now the quality control specification is an average of 1 flaw per garment, so in three garments this translates to an average of 3 flaws. The hypotheses of interest are
. Now the quality control specification is an average of 1 flaw per garment, so in three garments this translates to an average of 3 flaws. The hypotheses of interest are
![]()
Note that here we could state the null hypothesis as ![]() . However, as mentioned previously, the equality value is used for the calculation of the p-value, so it is sufficient to simply state the equality value in the null hypothesis. The observed number of flaws is 6, so the p-value is
. However, as mentioned previously, the equality value is used for the calculation of the p-value, so it is sufficient to simply state the equality value in the null hypothesis. The observed number of flaws is 6, so the p-value is
![]()
so the data provides insufficient evidence against the null hypothesis. We conclude based on this analysis that the quality control specifications are met.

