Example 6.2

George Kouretzis

Example 6.2

Estimation of the design bearing capacity of a single pile according to AS2159 using the α- and β-Methods - Multilayered soil profile case

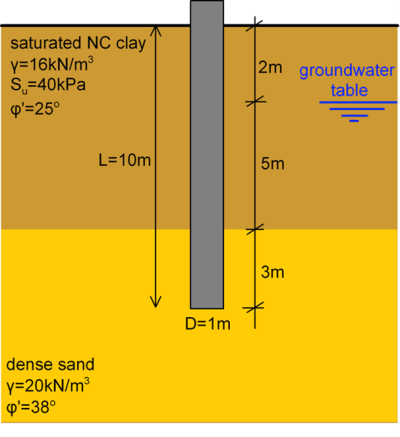
Determine the design bearing capacity of the concrete pile shown below, according to AS2159 provisions, using the simplified α– and β-Methods. For the specific problem, assume a basic geotechnical strength reduction factor φ_gb equal to φ_gb= 0.52. Ignore the weight of the pile.

Schematic of a pile in layered soil. The pile's length is 10m and its diameter is 1m. The water table is found at 2m from the ground surface. The properties of the top soil layer are: Thickness 7m, saturated NC clay, Su = 40 kPa, γ = 16 kN/m^3, φ'=25 deg. The properties of the bottom soil layer are: Dense sand of large thickness, γ = 20 kN/m^3, φ'=38 deg. — Example 6.2. Problem description and input parameters.

Answer:

Since the problem is asking us to find the design bearing capacity, we will consider that the pile is loaded with axial compressive load. The design bearing capacity of the pile must be determined both under short-term and long-term loading conditions, in order to establish the critical design bearing capacity. The top clay layer will behave as undrained under short-term loading, and as drained under long-term loading. On the other hand, the bottom dense sand layer will behave as drained under both long-term and short-term loading.

Estimation of the ultimate geotechnical strength under short-term conditions

1.1 Estimation of the skin friction resistance, Q_sf:

Clay layer (α-Method): According to Coduto (1994) (Figure 6.18a) for a uniform clay with S_u= 40 kPa it is a_u= 1.00. Moreover, following AS 2159, the first 1.5D meters of the pile shaft will not contribute to the friction resistance of the part of the pile embedded in the clay layer (Eq. 6.6):

${Q_{sf,clay}} = {a_u}{S_u}\pi D\left( {L - 1.5D} \right) = 1.0 \times 40 \times \pi \times 1 \times \left( {5.5} \right) = 691{\rm{\: kN}}$

Dense sand layer (β-Method): First, we have to calculate the vertical effective stress at the middle (z = 8.5 m) of the sand layer σ′_z0:

${\sigma '_{z0}} = {\sigma _{z0}} - u = \left( {7 \times 16 + 1.5 \times 20} \right) - 6.5 \times 10 = 77{\rm{ \:kPa}}$

In order to find the β factor, we estimate the earth pressure coefficient at-rest Κ₀ as (Eq. 6.16):

${K_0} = 1 - \sin \varphi ' = 0.384$

and the interface friction angle φ_i, which for a concrete pile with rough surface will be equal to 2/3 of the friction angle of the sand layer φ′ (Eq. 6.15):

${\varphi _i} = \dfrac{{2\varphi '}}{3} = {25.33^{\rm{o}}}$

Given the above, the β factor is calculated as (Eqs. 6.12-6.13):

$\beta = {K_0}\tan {\varphi _i} = 0.181$

and the skin friction resistance in terms of force of the part of the pile embedded in the dense sand layer will be equal to (Eq. 6.11):

${Q_{sf,sand}} = \beta {\sigma '_{z,0}}\pi DL = 0.181 \times 77 \times \pi \times 3 = 132{\rm{ \:kN}}$

It is interesting to note that the skin friction resistance in terms of stress f_sf at the middle of the sand layer is f_sf = 13.93 kPa. Considering the recommended values in Table 6.4, this is quite low, especially if we consider that the skin friction resistance in the overlying clay layer is f_sf = 40 kPa. However, observe that we have used the in situ lateral earth pressure in the calculations from Eq. 6.16. Had we followed API RP2A recommendations and considered K = 0.8 to 1 to account for installation effects, we would have calculated f_sf = Κtanφ_iσ′_z₀ = 1.0×0.473×77 = 36 kPa, which is considerably higher. This is an example where simplified methods, not accounting for installation effects, can provide over-conservative predictions.

1.2 Estimation of the end bearing resistance, Q_b

The pile toe is embedded in the dense sand layer, thus we will use Eq. 6.19 for drained loading conditions. First, we have to estimate the vertical effective stress at the pile toe level (z = 10m) σ′_z0,b:

${\sigma '_{z0,b}} = {\sigma _{z0,b}} - u = \left( {7 \times 16 + 3 \times 20} \right) - 8 \times 10 = 92{\rm{ \:kPa}}$

For the estimation of the bearing capacity factor N_qp we will use Eq. 6.19:

${N_{qp}} = {N_q} = {\tan ^2}\left( {{{45}^o} + \dfrac{{\varphi '}}{2}} \right){e^{\pi \tan \varphi '}} = 48.9$

The calculated N_qp value is quite high, still within the recommended zone of Figure 6.21. The end bearing resistance is calculated as:

${Q_b} = {N_{qp}}{\sigma '_{z0,b}}{A_b} = 48.93 \times 92 \times \pi \times {\left( {\dfrac{1}{2}} \right)^2} = 3535{\rm{ \:kN}}$

Note that if we use the expression recommended by Janbu (Eq. 6.20) to estimate the bearing capacity factor while considering a rational range of ψ_p values ψ_p= 75º to 85º we calculate bearing capacity factors ranging between N_qp≈ 32 to 42 and the corresponding end-bearing resistance will be Q_b≈ 2312 to 3034 kN. These values are compatible with the recommended N_qp values in Table 6.4.

1.3 Ultimate geotechnical strength (collapse load) under short-term conditions

The collapse load is the sum of the pile’s skin friction resistance along the clay and the sand layer, and its end bearing resistance:

${Q_f} = {Q_{sf,clay}} + {Q_{sf,sand}} + {Q_b} = 691 + 132 + 3535 = 4358{\rm{\: kN}}$

Notice that the over-conservative prediction of Q_sf,sand had little effect on the collapse load (about 5%), which is governed by the end bearing resistance of the pile’s toe in sand.

2. Estimation of the ultimate geotechnical strength under long-term conditions

2.1 Estimation of the skin friction resistance, Q_sf:

Clay layer (β-Method): We can divide the clay layer into two sublayers; one with thickness 2 m above the ground water table, and one with thickness 5 m below the groundwater table.

For the first sublayer (above the groundwater table):

vertical effective stress at the middle (z = 1.0 m) of sublayer 1 σ′_z0,1:

${\sigma '_{z0,1}} = {\sigma _{z0,1}} - {u_1} = 1 \times 16 - 0 = 16{\rm{ \:kPa}}$

lateral earth pressure coefficient (Eq. 6.15):

${K_0} = \left( {1 - \sin \varphi '} \right){\rm{OC}}{{\rm{R}}^{0.5}} = \left( {1 - \sin {{25}^{\rm{o}}}} \right) \times {1^{0.5}} = 0.577$

Interface friction angle φ_i for a rough concrete pile (Eq. 6.15):

${\varphi _i} = \dfrac{{2\varphi '}}{3} = {16.66^{\rm{o}}}$

β factor (Eqs. 6.12-6.13):

${\beta _1} = {K_0}{\rm{tan}}{\varphi _i} = 0.577 \times 0.299 = 0.172$

For the second sublayer (below the groundwater table):

vertical effective stress at the middle (z = 4.5 m) of sublayer 2 σ′_z0,2:

${\sigma '_{z0,2}} = {\sigma _{z0,2}} - {u_2} = 4.5 \times 16 - 2.5 \times 10 = 47{\rm{ \:kPa}}$

and ${\beta _2} = {K_0}{\rm{tan}}{\varphi _i} = 0.577 \times 0.299 = 0.172$

Using Eq. 6.14, the total skin friction resistance of the clay layer will be:

$\begin{array}{l}{Q_{sf,clay}} = {\beta _1} {{\sigma '}_{z0,1}} \pi D \left( {{L_1} - 1.5} \right) + {\beta _2} {{\sigma '}_{z0,2}} \pi D {L_2} = \\ = 0.172 \times 16 \times \pi \times 1 \times \left( {2 - 1.5} \right) + 0.172 \times 47 \times \pi \times 1 \times 5 = 131{\rm{ kN}}\end{array}$

Note that if we considered the clay layer as a single layer, and calculated the vertical effective stress at its middle (z = 3.5 m), we would calculate a total skin friction resistance Q_sf,clay= 122 kN.

If we assume the same ICP parameters for clay as in Example 6.1 (S_t = 1, φ_i = 25 deg) we would calculate according to the ICP method at the middle of the clay layer:

${\sigma '_{z0}} = {\sigma _{z0}} - u = \left( {2 \times 16 + 1.5 \times 6} \right) - 1.5 \times 10 = 26{\rm{ \:kPa}}$

${\sigma '_{he}} = {K_c}{\sigma '_{z0}} = 26\left[ {2.216} \right]{1.0^{0.42}}{\left[ {13} \right]^{ - 0.20}} = 34.5{\rm{ \:kPa}}$

${f_{sf}} = \left( {\dfrac{{{K_f}}}{{{K_c}}}} \right){\sigma '_{he}}\tan {\varphi _{i,f}} = 0.8 \times 34.5 \times 0.466 = 12.86{\rm{\: kPa}}$

${Q_{sf,clay}} = {f_{sf}}\pi D\left( {L - 1.5D} \right) = 12.86 \times \pi \times 1 \times \left( {7 - 1.5} \right) = 222{\rm{\: kN}}$

Therefore, unlike Example 6.1., here the ICP method provides considerably higher skin friction resistance for the clay layer, noting though that the ICP method is based on ESA concepts, and does not differentiate between long-term and short-term skin friction resistance.

As far as the skin friction resistance of the part of the pile embedded into the sand layer, it will be essentially the same as under short-term conditions:

${Q_{sf,sand}} = 132{\rm{ \:kN}}$

2.2 Estimation of the end-bearing resistance, Q_b:

The same applies for the end-bearing resistance of the pile toe embedded in sand: it will be the same as under short-term conditions:

${Q_b} = 3535{\rm{ \:kN}}$

2.3 Ultimate geotechnical strength (collapse load) under long-term conditions, Q_f:

The collapse load is the sum of the long-term pile’s skin friction resistance along the clay and the sand layer, and its end-bearing resistance:

${Q_f} = {Q_{sf,clay}} + {Q_{sf,sand}} + {Q_b} = 131 + 132 + 3535 = 3789{\rm{ \:kN}}$

3. Estimation of the design bearing capacity, φ_gbQ_f:

It appears that in this case, the long-term loading is critical, as it results in the lowest pile ultimate bearing capacity. The design bearing capacity according to AS2159 is calculated as:

${\varphi _{gb}}{Q_f} = 0.52 \times 3789 = 1970{\rm{ \:kN}}$

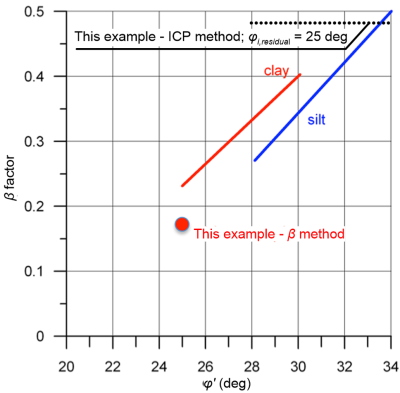
This is due to the long-term skin friction resistance in the clay layer being lower that the short-term skin friction resistance, and appears to be counterintuitive: As discussed in Part 5, we would expect the short term loading to be critical. However, comparisons with the ICP method have demonstrated that the α-method appears to be overestimating the skin friction resistance for soft-to-firm clays, and at the same time the β-method appears to be underestimating the skin friction resistance. Indeed, pile test results (Fellenius 1991) indicate that for clays and silts, the factor β usually ranges between 0.25 and 0.40 depending on their friction angle, as shown in Figure 6.44. In this example we have calculated β = 0.172 for the clay layer with φ′ = 25 deg, while the ICP method provides β = f_sf/σ′_z₀ = 12.86/26 = 0.49.

Graph showing the variation of the β factor with the friction angle of fine grained soils. Two curves for clay and silt are presented. The value of the β factor calculated in this example is depicted, and is significantly lower that the values suggested by the curves. The value calculated in the example with the ICP method, while considering φi,residual = 25 deg, is also shown. — Figure 6.44. Comparison of results with β factor for clays and silts estimated according to Fellenius (1991).

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Answer:

License

Share This Book