Example 6.16

George Kouretzis

Example 6.16

Estimation of the p-y curve reduction factor for a laterally loaded pile group

Determine the reduction factor β_g⁵ for pile #5 shown in the figure below, when the lateral load acts along the weak axis of the group (X-X), and along the strong axis of the group (Y-Y). The diameter of all piles is equal to D.

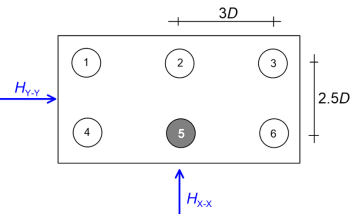
Diagram of a rectangular layout with six circular points labeled 1-6, highlighting point 5 in the center, with dimensions and directional arrows. — Example 6.16. Problem description and input parameters.

1. Load along the weak axis, H_X-X :

Interaction of pile #5 with all the remaining piles in the group must be considered, according to Eq. 6.166 and Figure 6.130, as:

$\beta _g^5 = \begin{array}{*{20}{l}}{\beta _{g,s}^{5 \leftrightarrow 4}{\rm{ }}\left( {{\rm{side \: by \:side}}} \right)}\\{ \times \beta _{g,s}^{5 \leftrightarrow 6}{\rm{ (side \:by \:side)}}}\\{ \times \beta _{g,l}^{5 \leftrightarrow 2}{\rm{ (leading \:in \:line)}}}\\{ \times \beta _{g,sk}^{5 \leftrightarrow 1}{\rm{ (leading \:skewed)}}}\\{ \times \beta _{g,sk}^{5 \leftrightarrow 3}{\rm{(leading \:skewed)}}}\end{array}$

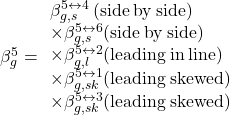
The individual interaction factors are determined from Figures 6.127–6.129 as:

$\beta _{g,s}^{5 \leftrightarrow 4} = \beta _{g,s}^{5 \leftrightarrow 6} = 0.64 \times {3^{0.34}} = 0.929$

$\beta _{g,l}^{5 \leftrightarrow 2} = 0.70 \times {2.5^{0.26}} = 0.888$

$\left( \begin{array}{l}\beta _{g,a}^{5 \leftrightarrow 1} = 1.0\\\beta _{g,b}^{5 \leftrightarrow 1} = 0.7{\left( {\sqrt {{3^2} + {{2.5}^2}} } \right)^{0.26}} = 0.997\\\omega = {\tan ^{ - 1}}\left( {\dfrac{3}{{2.5}}} \right) = 50.2{\rm{ \:deg}}\end{array} \right) \to \beta _{g,sk}^{5 \leftrightarrow 1} = \beta _{g,sk}^{5 \leftrightarrow 3} = \sqrt {{{0.997}^2}{{\cos }^2}\left( {50.2} \right) + {1^2}{{\sin }^2}\left( {50.2} \right)} = 0.998$

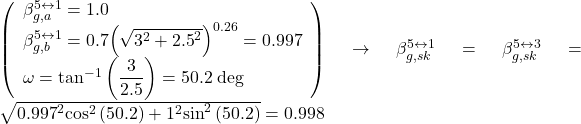
The reduction factor for pile #5 is calculated from Eq. 6.166 as:

$\beta _g^5 = \beta _{g,s}^{5 \leftrightarrow 4} \times \beta _{g,s}^{5 \leftrightarrow 6} \times \beta _{g,l}^{5 \leftrightarrow 2} \times \beta _{g,sk}^{5 \leftrightarrow 1} \times \beta _{g,sk}^{5 \leftrightarrow 3} = 0.929 \times 0.929 \times 0.888 \times 0.998 \times 0.998 = 0.763$

2. Load along the strong axis, H_Y-Y :

The procedure is similar, but notice that the relative position of the pile compared to its neighboring piles must be re-assessed according to Figure 6.130, as:

$\beta _g^5 = \begin{array}{*{20}{l}}{\beta _{g,s}^{5 \leftrightarrow 4}{\rm{ }}\left( {{\rm{trailining\: in \:line}}} \right)}\\{ \times \beta _{g,s}^{5 \leftrightarrow 6}{\rm{ (leading \:in \:line)}}}\\{ \times \beta _{g,l}^{5 \leftrightarrow 2}{\rm{ (side \:by \:side)}}}\\{ \times \beta _{g,sk}^{5 \leftrightarrow 1}{\rm{ (trailing \:skewed)}}}\\{ \times \beta _{g,sk}^{5 \leftrightarrow 3}{\rm{(leading \:skewed)}}}\end{array}$

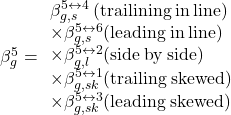
The individual interaction factors are determined from Figures 6.127–6.129 as:

$\beta _{g,s}^{5 \leftrightarrow 4} = 0.48 \times {3^{0.38}} = 0.728$

$\beta _{g,s}^{5 \leftrightarrow 6} = 0.70 \times {3^{0.26}} = 0.931$

$\beta _{g,l}^{5 \leftrightarrow 2} = 0.64 \times {2.5^{0.34}} = 0.874$

$\left( \begin{array}{l}\beta _{g,a}^{5 \leftrightarrow 1} = 1.0\\\beta _{g,b}^{5 \leftrightarrow 1} = 0.48{\left( {\sqrt {{3^2} + {{2.5}^2}} } \right)^{0.39}} = 0.805\\\omega = {\tan ^{ - 1}}\left( {\dfrac{{2.5}}{3}} \right) = 39.8{\rm{ \:deg}}\end{array} \right) \to \beta _{g,sk}^{5 \leftrightarrow 1} = \sqrt {{{0.805}^2}{{\cos }^2}\left( {39.8} \right) + {1^2}{{\sin }^2}\left( {39.8} \right)} = 0.890$

$\left( \begin{array}{l}\beta _{g,a}^{5 \leftrightarrow 3} = 1.0\\\beta _{g,b}^{5 \leftrightarrow 3} = 0.70{\left( {\sqrt {{3^2} + {{2.5}^2}} } \right)^{0.26}} = 0.997\\\omega = {\tan ^{ - 1}}\left( {\dfrac{{2.5}}{3}} \right) = 39.8{\rm{ \:deg}}\end{array} \right) \to \beta _{g,sk}^{5 \leftrightarrow 1} = \sqrt {{{0.997}^2}{{\cos }^2}\left( {39.8} \right) + {1^2}{{\sin }^2}\left( {39.8} \right)} = 0.998$

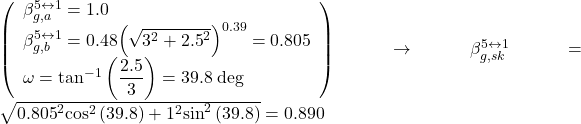
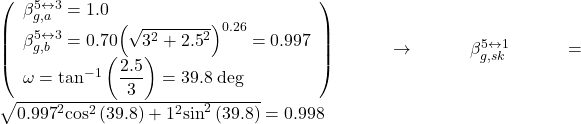
The reduction factor for pile #5 is calculated from Eq. 6.166 as:

$\beta _g^5 = \beta _{g,s}^{5 \leftrightarrow 4} \times \beta _{g,s}^{5 \leftrightarrow 6} \times \beta _{g,l}^{5 \leftrightarrow 2} \times \beta _{g,sk}^{5 \leftrightarrow 1} \times \beta _{g,sk}^{5 \leftrightarrow 3} = 0.728 \times 0.931 \times 0.874 \times 0.890 \times 0.998 = 0.526$

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

License

Share This Book