Example 6.10
Calculation of settlement of a group of piles connected with rigid and flexible pile cap
Consider the floating pile group depicted in the figure below, consisting of six concrete piles of diameter D = 300 mm driven into a deep clay layer. The group is subjected to a vertical compressive load Qw,group = 3000 kN. A load test was performed on a single pile, and resulted in settlement of 15 mm under load 500 kN. The ratio of the Young’s modulus of the pile over the Young’s modulus of the clay is Ep/Es = 2000. Determine the immediate settlement of the pile group if i) the pile cap is rigid, and ii) the pile cap is flexible.
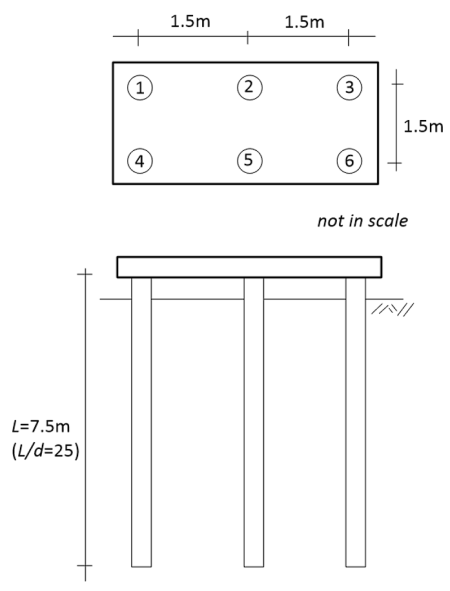
We need first to determine the pile stiffness factor Kp from Eq. 6.93. Since the piles are solid it is Kp = Ep/Es = 2000.
Corner piles 1, 3, 4 and 6 will behave identically, and we will call them Pile Type A. Mid piles 2 and 5 will also behave identically, and we will call them Pile Type B. We will also denote the serviceability load on piles A is B as QA and QB, respectively.
We can find the interaction factors αi,ij from the chart in Figure 6.77 for L/D = 25, interpolating between Kp = 1000 and Kp =∞. We need interaction factors for two piles types: Pile Type A (e.g. for Pile 1) and Pile Type B (e.g. for Pile 2).
| PIle j | Pile 1 (Pile type A) | Pile 2 (Pile type B) | ||
|---|---|---|---|---|
| s/D | αi,ij | s/D | αi,ij | |
| 1 | 0 | – | 5 | 0.42 |
| 2 | 5 (i.e., 1500 mm/300 mm) | 0.42 | 0 | – |
| 3 | 10 | 0.27 | 5 | 0.42 |
| 4 | 5 | 0.42 | 7.07 | 0.35 |
| 5 | 7.07 | 0.35 | 5 | 0.42 |
| 6 | 11.2 | 0.25 | 7.07 | 0.35 |
We can now cast Eq. 6.100 for all piles. It is:
Settlement of pile 1 (and all Type A piles), ρΑ:
![Rendered by QuickLaTeX.com {\rho _A} = {\rho _1}\left[ {{Q_A}\left( {0.27 + 0.42 + 0.25} \right) + {Q_B}\left( {0.42 + 0.35} \right) + {Q_A}} \right] \to \dfrac{{{\rho _A}\,}}{{{\rho _1}}} = 1.94{P_A} + 0.77{P_B}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-be5274c30cd503aee41be9d282394144_l3.png)
Settlement of pile 2 (and all Type B piles), ρB:
![Rendered by QuickLaTeX.com {\rho _B} = {\rho _1}\left[ {{Q_A}\left( {0.42 + 0.42 + 0.35 + 0.35} \right) + {Q_B}\left( {0.42} \right) + {Q_B}} \right] \to \dfrac{{{\rho _B}\,}}{{{\rho _1}}} = 1.54{P_A} + 1.42{P_B}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-c9a4b0476ef6f90d716fa2db2eaee585_l3.png)
In addition, the force equilibrium Eq. 6.101 is:
![]()
We have three equations, with four unknowns, the two settlements and the two loads acting on each pile type. So we need one more equation.
Case 1: Piles connected with a rigid pile cap
In this case the extra equation results from considering that the settlement of all piles will be the same, therefore ρΑ/ρ1 = ρΒ/ρ1. In addition, settlement of a pile under unit load ρ1 is ρ1 = 15/500 = 0.03 mm/kΝ. As such:
![]()
and
![]()
![]()
![]()
As expected, when the pile cap is rigid the corner piles are carrying larger axial loads, relatively to the mid piles.
![]()
![]()
Note that for a six-pile group (n = 6) and Φ = 0.5 Eq. 6.96 yields Rs = 2.44. In other words, the simplified method of Flemming et al. predicts that settlement of each pile, carrying load 3000/6 = 500 kN, will be 500 x 0.03 x 2.44 = 36.6 mm. The advantage of this, more rigorous, method, apart of course of considering the distribution of the vertical load on piles, is that it does not require assuming a value for the factor Φ.
Case 2: Piles connected with a flexible pile cap
If the piles are connected with a flexible pile cap, we can assume that they will all be carrying the same vertical load. Therefore our fourth equation is QA = QB = 500 kN. Accordingly:
![]()
![]()
![]()
![]()
Notice that there is some differential settlement between piles connected with a flexible cap, with the mid piles 2 and 5 (Piles B) settling, as expected, more. This differential settlement may be important, and should be considered in the design of the pile group.

