"

Example 6.1

Estimation of the design bearing capacity of a pile according to AS2159 using the α-Method and the ICP method

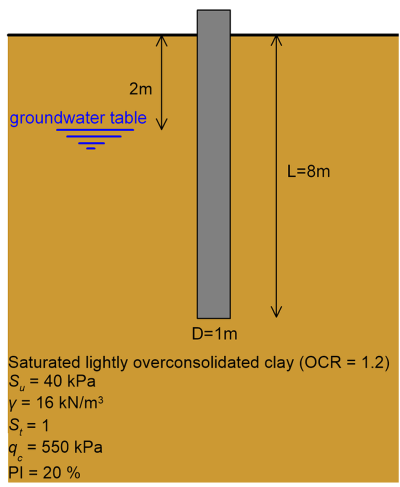
Determine the short-term design bearing capacity of the single cylindrical pile driven in a uniform clay layer, according to AS 2159 provisions. For the specific problem, assume a basic geotechnical strength reduction factor φgb equal to φgb = 0.60. Ignore the weight of the pile.

Schematic of a friction pile in uniform soil. The pile's length is 8m and its diameter is 1m. The water table is found at 2m from the ground surface. The properties of the foundation soil are: Saturated lightly overconsolidated clay (OCR = 1.2), Su = 40 kPa, γ = 16 kN/m^3, St =1, qc = 550 kPa, PI = 20%.
Example 6.1. Problem description and input parameters.

Answer:

Since the problem is asking us to find the design bearing capacity, we will consider that the pile is loaded with axial compressive load. A saturated clay layer will behave as undrained under short-term loading. The pile bearing capacity will be determined first using the α-Method, employing a total stress analysis (TSA). Remember that during a total stress analysis, the groundwater table level does not affect the calculations. In fact, the only soil parameter required by the α-method is the undrained shear strength Su.

1. Estimation of the skin friction resistance, Qsf with the α-method:

Following Tomlinson (1987) for L/D = 8 and uniform clay with Su = 40kPa (Figure 6.18b), the adhesion factor is estimated to be au = 0.95. Alternatively, according to Coduto (1994) (Figure 6.18a) for a uniform clay with Su=40 kPa it is au = 1.00. We will estimate the skin friction resistance while adopting the slightly more conservative value au = 0.95. Following AS2159, the first 1.5D meters of the pile shaft will not contribute to the skin friction resistance, thus Eq. 6.6 yields:

{Q_{sf}} = {a_u}{S_u}\pi D\left( {L - 1.5D} \right) = 0.95 \times 40 \times \pi \times 1 \times \left( {8 - 1.5} \right) = 776{\rm{ \:kN}}

2. Estimation of the end bearing resistance, Qb with the α-method:

Using Eq. 6.9 for Su > 25 kPa:

{Q_b} = {N_{cp}}{S_{u,b}}{A_b} = 9 \times 40 \times \pi {\left( {\dfrac{D}{2}} \right)^2} = 282.7{\rm{ \:kN}}

As the skin friction resistance is higher than 80% of the end-bearing resistance, the pile is classified as friction pile.

3. Estimation of the design bearing capacity φgbQf with the α-method:

Since we seek to estimate the design bearing capacity (i.e., pile subjected to axial compressive loads) the collapse load (ultimate geotechnical strength) of the pile is the sum of its skin friction and end-bearing resistance:

{Q_f} = {Q_{sf}} + {Q_b} = 1059{\rm{ \:kN}}

According to AS2159, the design bearing capacity of the pile is calculated as:

{\varphi _{gb}}{Q_f} = 0.60 \times 1059 = 635{\rm{ \:kN}}

Notice that the skin friction resistance of this pile contributes approximately 73% of total strength, which is expected for friction piles in clay. Nevertheless, the skin friction resistance predicted with TSA is fsf = 0.95 x 40 = 38 kPa is quite high. Let’s repeat the calculations using this time the ICP method (Section 6.12.7).

4. Estimation of the skin friction resistance, Qsf with the ICP method:

We will estimate first the skin friction resistance with Eq. 6.49. For that we need to know the interface friction angle at failure φi,f. Let’s assume conservatively that the residual friction angle will govern the skin friction resistance. From Figure 6.29 and for PI = 20 % we obtain from the best fit line φi,f = φi,residual = 25 deg. At the middle of the pile (h/R = 4/0.5 = 8, Figure 6.25) the geostatic vertical effective stress is:

{\sigma '_{z0}} = 16 \times 2 + \left( {16 - 10} \right) \times 2 = 44{\rm{ \:kPa}}

and the normal stress acting at the soil-pile interface prior to pile loading σ′he is calculated from Eq. 6.50 as:

{\sigma '_{he}} = {K_c}{\sigma '_{z0}} = 44\left[ {2.2352} \right]{1.2^{0.42}}{\left[ 8 \right]^{ - 0.20}} = 70{\rm{ \:kPa}}

Therefore the skin friction resistance from Eq. 6.49 is:

{f_{sf}} = \left( {\dfrac{{{K_f}}}{{{K_c}}}} \right){\sigma '_{he}}\tan {\varphi _{i,f}} = 0.8 \times 70 \times 0.466 = 26.1{\rm{ \:kPa}}

Compare fsf calculated with the ICP method (26.1 kPa) and the fsf calculated with the α-method: there is important difference, suggesting that the α-method, which is based on TSA, provides relatively high values of skin friction resistance, compared with the ICP method which is based on ESA principles (undrained strength is not an input parameter) and explicitly accounts for installation effects. The skin friction resistance predicted with the ICP method is accordingly calculated as:

{Q_{sf}} = {f_{sf}}\pi D\left( {L - 1.5D} \right) = 26.1 \times \pi \times 1 \times \left( {8 - 1.5} \right) = 533{\rm{ \:kN}}

5. Estimation of the end bearing resistance, Qb with the ICP method:

For closed-end piles and short-term loading conditions, the end-bearing resistance in terms of stress qbf is calculated from Eq. 6.51, as function of the average cone resistance. Here we are considering for simplicity constant cone resistance qc = 550 kPa (compatible with undrained strength of Su = 40 kPa according to the interpretation methods presented in Part 1). Therefore the end bearing resistance is:

{q_{bf}} = 0.8{q_{c\left( {av} \right)}} = 440{\rm{ \:kPa}}

and the end-bearing resistance in terms of force is calculated from Eq. 6.30 as:

{Q_b} = \left( {\dfrac{{\pi {D^2}}}{4}} \right){q_{bf}} = 345.6{\rm{ \:kN}}

Notice that Qb calculated with the ICP method (345.6 kN) is only slightly higher compared to that calculated with the α-method. Jardine et al. (2005) discuss that indeed the ICP method provides comparable end bearing resistance values to the α-method.

6. Estimation of the design bearing capacity φgbQf with the ICP method:

As before, the collapse load (ultimate geotechnical strength) of the pile is the sum of its skin friction and end bearing resistance:

{Q_f} = {Q_{sf}} + {Q_b} = 878.6{\rm{ \:kN}}

According to AS2159, the design bearing capacity of the pile is calculated as:

{\varphi _{gb}}{Q_f} = 0.60 \times 878.6 = 527.1{\rm{ \:kN}}

The conclusion from this exercise, where the design bearing capacity calculated with the ICP method is 17% lower compared to that calculated with the α-method is that simplified methods (which require only one input parameter i.e., the undrained shear strength) do not always provide conservative predictions.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book