Example 5.7

George Kouretzis

Example 5.7

Design capacity from in situ tests: CPT

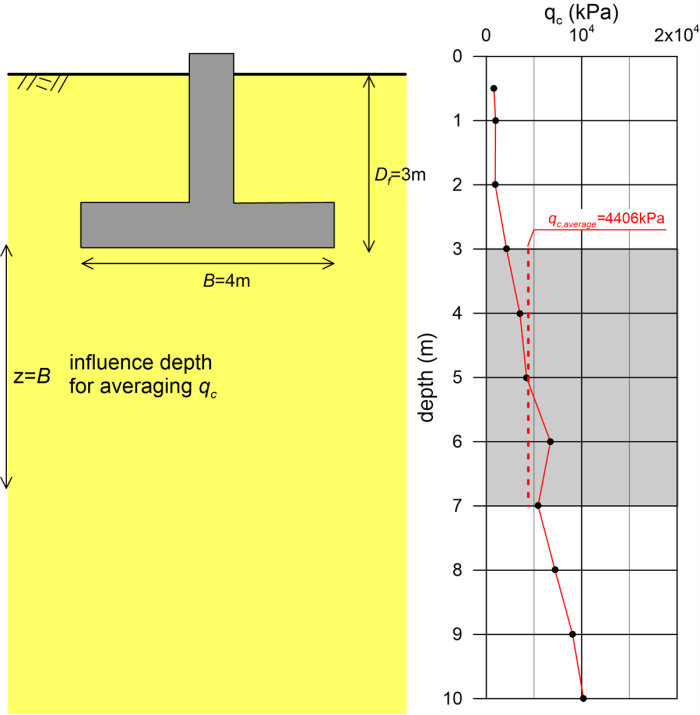
Estimate the design capacity of the strip footing shown below according to AS 5100.3-2, directly from CPT measurements. The foundation subsoil is classified as silty sand (SBT=5/6 from the soil behavior type chart of Figure 1.28).

The figure on the left presents a footing of width B = 4 m embedded in soil at depth Df = 3 m. The influence depth for averaging qc is identified as z = B, measured from the footing's base. The figure on the right presents the variation of cone resistance qc with depth, from the ground surface up to a depth of 10 m. The average qc along the influence depth is calculated to be qc,average = 4406 kPa. — Example 5.7. Problem description and input parameters.

Answer:

The average cone resistance along a depth z = B = 4 m below the footing foundation level (-3m) is q_c,average = 4.4 MPa (average of 5 values). Considering conservatively K_φ = 0.16 as per above, and substituting to Eq. 5.54 yields:

${q_f} = {K_\varphi }{q_{c,average}} = 700{\rm{ \:kPa}}$

Note that the measured cone resistance in this sand is relatively low, and according to Table 1.8 the average N₆₀ value along the influence depth is N₆₀ = (q_c,average/p_a)/3.0 = 14.6 therefore the sand is classified as medium dense (Table 1.3).

As the bearing capacity is determined from CPT test results, the appropriate range of the geotechnical strength reduction factor φ_gfrom Table 5.1 is φ_g= 0.40 to 0.50. Selecting conservatively the lower bound of the proposed range, the design capacity in terms of stress in terms of force per running meter of the strip footing is determined as:

${\varphi _g}{q_f} \ge {S^ * }$