"

Example 5.6

Design capacity from in situ tests: SPT

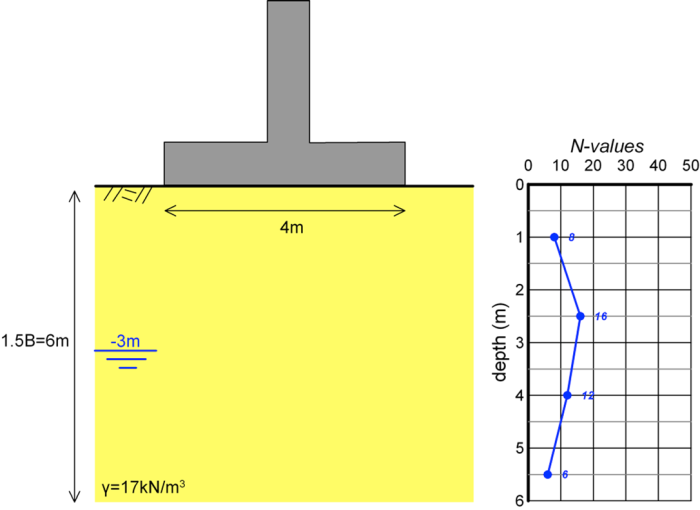
Estimate the design capacity of the footing shown below according to AS 5100.3, using directly the SPT measurements in the loose-to-medium sandy foundation soil.

The figure on the left presents a footing of width 4 m resting on the soil surface. The groundwater table is found at -3m from the surface. The unit weight of soil is γ = 17 kN/m^3. The total soil thickness considered is 1.B = 6 m. The figure on the right presents the variation of N-values with depth, up to a depth of 5.5 m. N-values range from N = 6 to N = 16.
Example 5.6. Problem description and input parameters.

Answer:

Before applying Eq. 5.53 to estimate the bearing capacity, we must first find the corrected N′ values for overburden stress, and the average corrected value N′ over a depth 1.5B = 6 m. Application of Eqs. 5.51 and 5.52 for calculating the overburden stress correction factor CN and accordingly the average N′ value for 6 m is presented in the table below.

Example 5.6. Calculation of average N′  value.
Depth (m) N Total stress (kPa) Pore pressure (kPa) Effective stress (kPa) CN N′ = NCN
1 8 17 0 17 2.373 2.0* 16
2.5 16 42.5 0 42.5 1.501 24
4 12 68 10 58 1.285 15.4
5.5 6 93.5 25 68.5 1.182 7.1
N’average 15.62

*Note: Use of CN values higher than 2.0 is not recommended

Substituting in Eq. 5.53 while taking the groundwater table factors Cw1, Cw2 from Table 5.7 yields:

{q_f} = 9.57{N'_{average}}B\left( {1.0 + 1.0 \times \dfrac{0}{4}} \right) = 598{\rm{ \:kPa}}

As the bearing capacity is determined from SPT test results, the appropriate range of the geotechnical strength reduction factor φg from Table 5.1 is φg = 0.35 to 0.40. Selecting conservatively the lower bound of the proposed range, the design capacity is determined in terms of stress as:

{\varphi _g}{q_f} \ge {S^ * } \Rightarrow 0.35 \times 598 \ge {S^ * } \Rightarrow {S^ * } \le {\rm{209 \:kPa}}

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book