"

Example 5.4

Design capacity of a footing resting on a two-layer formation according to AS5100.3

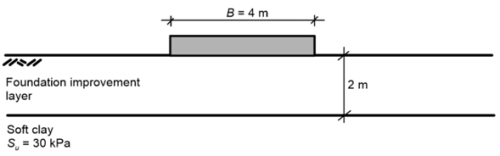
A strip footing, considered to be infinitely long for practical purposes, will be founded on the surface of a soft saturated clay layer. The undrained shear strength of the clay was measured in the laboratory to be Su = 30 kPa. To increase the bearing capacity, the Geotechnical Engineer proposed to lay on top of the soft clay a 2m-thick layer of well-compacted coarse-grained material. Assuming a punching-type failure mechanism and vertical-only loading, estimate the design capacity of the footing under short-term conditions, according to AS 5100.3. The geotechnical strength reduction factor is equal to φg = 0.45.

Schematic of a footing resting on the surface of a foundation improvement layer. The width of the footing is B = 4 m. The thickness of the foundation improvement layer is 2 m, measured from the surface. Underneath the improvement layer there is a soft clay layer with Su = 30 kPa.
Example 5.4. Problem description and input parameters.

Answer:

We will consider only the punching failure mechanism here, and we will not estimate the design capacity considering uniform soil with the properties of the foundation improvement layer mentioned in Section 5.5.3, as it will not be critical. A well-compacted improvement layer will exhibit much higher shear strength, compared to the soft clay layer.

Schematic of an equivalent footing embedded in a foundation improvement layer, at depth Df,eq equal to the thickness of the improvement layer. The width of the equivalent footing is B = 4 m. The thickness of the foundation improvement layer is 2 m, measured from the surface. Underneath the improvement layer there is a soft clay layer with Su = 30 kPa.
Figure 5.42. Geometry of the equivalent footing resting on the top of the soft clay layer.

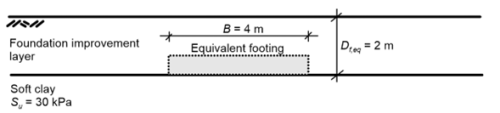
First, following the simplified method presented in Section 5.5.3, we estimate the bearing capacity of a vertically loaded equivalent strip footing under short-term undrained conditions, assuming it is founded on the improvement layer-soft clay interface (Figure 5.42). The embedment depth of this equivalent footing is Df = 2 m, its width is equal to the width of the real footing B = 4 m and its length is infinite L= ∞.

The short-term net bearing capacity of the equivalent strip footing qeq is calculated from Eq. 5.24 as:

{q_{eq}} = \left( {5.14{S_u}} \right){s_c}{d_c}

While the shape, sc and embedment, dc factors can be calculated from Table 5.5 as:

{s_c} = 1 + 0.2\left( {\dfrac{{B'}}{{L'}}} \right) = 1.0{\rm{ \:since \:}}L = \infty

{d_c} = 1 + 0.33\arctan \left( {\dfrac{{{D_f}}}{{B'}}} \right) = 1 + 0.33 \times 0.463{\rm{\:rad}} = 1.153

and the short-term net bearing capacity of this equivalent footing is:

{q_{eq}} = \left( {5.14{S_u}} \right){s_c}{d_c} = 177.8{\rm{ \:kPa}}

The pressure q that must be applied on the real footing to transfer vertical stress at the improvement layer-soft clay interface equal to the net bearing stress of the equivalent footing qeq is calculated from Eq. 5.41 as:

\Delta {\sigma _z} = {q_{eq}} = q\left[ {\dfrac{B}{{\left( {B + z} \right)}}} \right] \Rightarrow q = \dfrac{{\left( {B + z} \right)}}{B}{q_{eq}} = \left( {\dfrac{{4 + 2}}{4}} \right)177.8 = 266.7{\rm{ \:kPa}}

As application of the pressure q on the real footing results in shear failure developing into the soft clay layer, q will be equal to the net bearing capacity of the real footing. Moreover, as the real strip footing is constructed directly on the surface of the improvement layer, its design capacity in terms of load per running meter according to AS 5100.3 will be:

{\varphi _g}q + \gamma {D_f} \ge {S^ * }

0.45 \times 266.7 + 0 \ge {S^ * }

{S^ * } \le 120{\rm{\:kPa}}

{S^ * } \le 120{\rm{\:kPa}} \times \left( {4 \times 1} \right){{\rm{m}}^{\rm{2}}} = 480{\rm{ \:kN}}/{\rm{running \:meter \:of \:footing}}

Let’s now estimate the design capacity again, using this time the method of Salimi Eshkevari et al. (2019a). For that we need two more parameters: The unit weight γ and the friction angle φ′ of sand. We will assume here that γ = 20 kN/m3 and φ′ = 40 deg. The coefficients of Eq. 5.43 are calculated from Eqs. 5.44 and 5.45 as:

\alpha = 0.039\ln \left( {\tan {{40}^{\rm{o}}}} \right) - 0.164 = - 0.1708

\beta = 0.597\ln \left( {\tan {{40}^{\rm{o}}}} \right) - 0.051 = - 0.1557

and

\theta ({\rm{rad}}) = \left( { - 0.1708} \right)\ln \left( {\dfrac{{30}}{{20 \times 2}}} \right) - 0.1557 = - 0.1065

In other words, the width of the equivalent footing is B + 2Htanθ = 3.572 m < 4 m.

The coefficient δ required to calculate the punching shear coefficient Ksr is:

\delta = - 3.45\left( {\tan {{40}^{\rm{o}}}} \right) + 8.693 = 5.798

Thus:

{K_{sr}} = \delta \left( {\dfrac{{{S_u}}}{{\gamma H}}} \right) + 2 = 6.348

The bearing capacity of the strip footing on sand over clay is calculated from Eq. 5.42 as:

{q_{f,l}} = \dfrac{1}{B}\left( {\gamma {H^2}{K_{sr}}\tan \varphi ' + {N_c}{S_u}\left[ {B + 2H\tan \theta } \right] + \gamma {H^2}\tan \theta } \right) = \dfrac{1}{4}\left( {426.12 + 550.86 - 8.552} \right) = 242{\rm{ \:kPa}}

Therefore, its design capacity in terms of load per running meter according to AS 5100.3 will be:

{\varphi _g}{q_{f,l}} + \gamma {D_f} \ge {S^ * }

0.45 \times 242 + 0 \ge {S^ * }

{S^ * } \le 108.9{\rm{\:kPa}}

{S^ * } \le 108.9{\rm{\:kPa}} \times \left( {4 \times 1} \right){{\rm{m}}^{\rm{2}}} = 435{\rm{ kN}}/{\rm{running \:meter \:of \:footing}}

Observe that, while the results of the two method are generally compatible, the simplified method overestimates the bearing capacity in the problem at hand. That is because the width of the equivalent footing is not equal to the width of the actual footing, but rather it is shorter.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book