"

Example 4.4

Estimation of a 1-D primary consolidation settlement using the results of an oedometer test

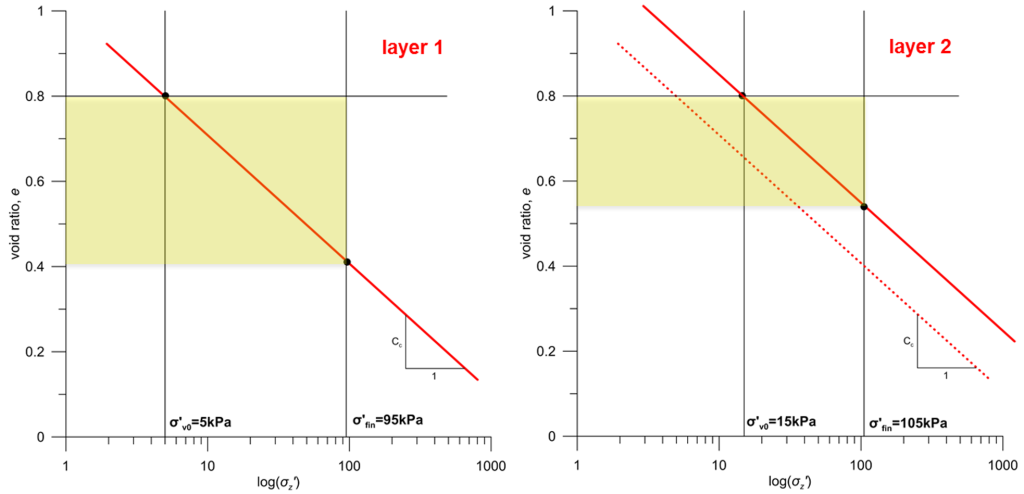
Calculate again the primary consolidation settlement due to the strip pressure, using this time the oedometer test results depicted in the figure.

Graph showing a pressure q_ext = 90 kPa of width B = 16 m applied on the surface of a normally consolidated clay layer of thickness H = 4 m. The properties of the clay layer are e0 = 0.8, Cc = 0.10, γ = 15 kN/m^3. The clay layer is underlaid by very dense gravelly sand, denoted as incompressible. The water table is at the ground surface.
Example 4.4. Problem description and input parameters.

Answer:

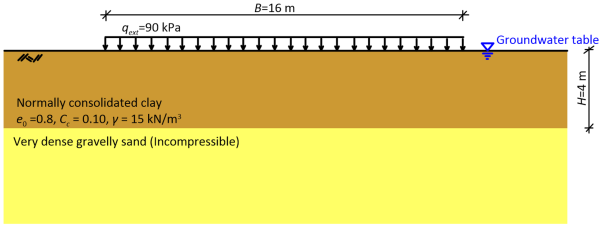
As discussed in Example 4.3, the width of the loaded area is large, compared to the thickness of the compressible layer so we can well assume 1-D consolidation conditions. The additional effective stress Δσ′z due to the application of the pressure will be equal to the applied pressure Δσ′z = qext = 90 kPa.

To improve accuracy when the problem involves rather thick compressible layers (H > 2 m) and we are using non-linear consolidation theory, we can divide the layer into sublayers, and find the settlement of each sublayer (Figure 4.33) separately.

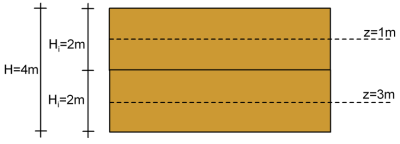
Graph showing division of a 4m-thick soil layer into two 2m-thick sublayers. The mid point of the top sublayer is at z = 1 m and the mid point of the bottom sublayer is at z = 4 m.
Figure 4.33. Dividing the compressible layer into two sublayers.

Accordingly, we sum individual settlements to find the settlement of the entire compressible layer. In the corresponding equations, H will be the thickness of each sublayer (Hi), and the effective stresses will be calculated at the middle of each sublayer.

As the clay is normally consolidated, we will apply Eq. 4.34 for the estimation of the settlement of each sublayer. The necessary calculations are presented in the table below:

Example 4.4. Settlement calculation. 
Geostatic total stress σz0 = γz Hydrostatic pore pressure u0 = γwz Geostatic effective stress σ′z0 = σz0 – u0 Final effective stress σ′fin = σ′z0 + qext log(σ′fin/σ′z0) Settlement of each sublayer, ρpc
Sublayer 1 (Hi = 2m) 15 kPa 10 kPa 5 kPa 95 kPa 1.278 0.14 m
Sublayer 2 (Hi = 2m) 45 kPa 30 kPa 15 kPa 105 kPa 0.845 0.09 m
Total settlement: 0.23 m

As expected, settlement of sublayers 1 and 2 is not equal, as the preconsolidation stress (equal in this case to the initial, geostatic effective stress as the clay is normally consolidated) increases with depth, while the applied pressure on both is 90 kPa. This is illustrated in the figure below, where the path followed by a soil element at the middle of each sublayer is presented, and is a consequence of introducing soil non-linear response in consolidation calculations.

The graph on the left shows the stress path followed by a soil element found at the mid of the top layer 1 in the void ratio e -log σ'_z space. The initial void ratio is 0.8 and the initial stress is 5 kPa. The final void ratio is 0.4 and the final stress is 95 kPa. The graph on the right shows the stress path followed by a soil element found at the mid of the bottom layer 2 in the void ratio e -log σ'_z space. The initial void ratio is 0.8 and the initial stress is 15 kPa. The final void ratio is approximately 0.52 and the final stress is 105 kPa.
Example 4.4. Stress paths followed by soil elements at the middle of layer 1 and layer 2.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book