"

3.6 Stresses in the soil due to a rectangular pressure

The common case of a rectangular footing transferring vertical loads from the structure to the soil is neither a plane-strain nor an axisymmetric problem, as the ones discussed above (Figure 3.9). Therefore, finding the exact distribution of additional stresses with depth resulting from a rectangular pressure acting on the surface of a homogeneous elastic half-space requires some perhaps cumbersome mathematical manipulations.

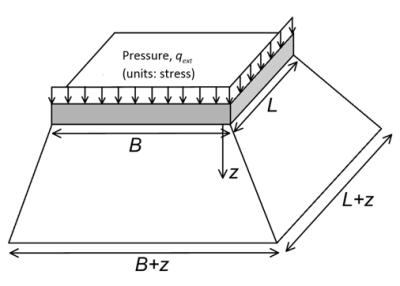
Diagram illustrating a rectangular pressure of dimensions B x L, distributed with depth z with an approximate 2:1 distribution.
Figure 3.9. Rectangular pressure acting on the surface of a homogeneous elastic half-space.

If we assume 2:1 distribution of stresses in the half-space (Figure 3.9) we can obtain an approximation of the additional vertical stress Δσz at any depth z, as:

(3.15)  \Delta {\sigma _z} = \dfrac{{{q_{ext}}BL}}{{\left( {B + z} \right)\left( {L + z} \right)}}

The above Eq. 3.15, albeit approximate, will provide reasonably accurate results for depths z > B.

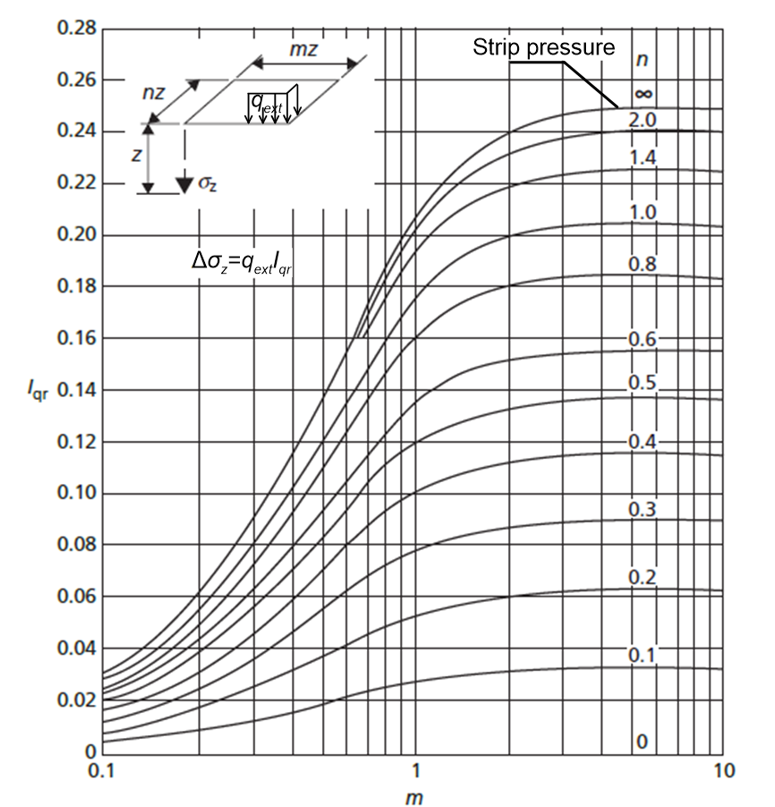
Vertical stress increments under the corner of a rectangular pressure can be calculated using the so-called Fadum charts. Such a chart providing the factor Iqr = Δσz/qext is presented in Figure 3.10. The use of this chart for calculating vertical stresses for geometries other than that illustrated in Figure 3.10 is discussed later in Chapter 3.7.

Graph plotting the variation of the factor Iqr at depth z with the parameter m (mz is the width of the rectangular pressure), for different values of the parameter n (nz is the length of the rectangular pressure). The formula providing the additional vertical stress at the edge of the pressure is Δσ_z=q_ext x I_qr.
Figure 3.10. Values of influence factor Iqr to calculate vertical stress increments underneath the edge of a rectangular area of dimensions nz x mz on which a vertical pressure qext is applied (after Fadum 1948).

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book