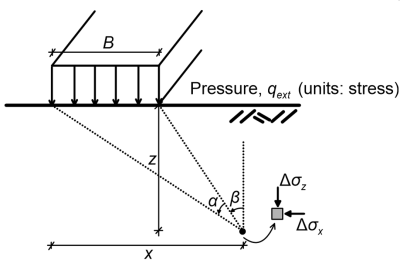
3.4 Stresses in the soil due to a strip pressure
Stresses applied on the soil surface e.g., from a footing of “infinite” length can be modelled as an infinitely long (strip) pressure acting on the surface of a homogeneous elastic half-space (Figure 3.7a). As plane-strain symmetry conditions apply, additional stresses due to the application of the pressure qext can be calculated as:
(3.10) ![]()
(3.11) ![]()
(3.12) ![]()
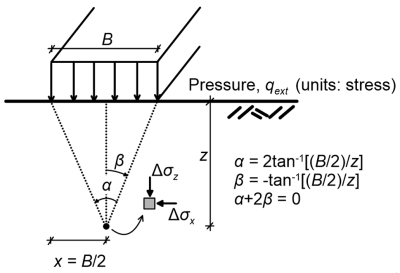
Τhe stress increment components and angles α and β are defined in Figure 3.6a. Angles α and β must be input in Eqs. 3.10 to 3.12 in radians, not in degrees, and may attain negative values too, as shown in Figure 3.7b.

