"

3.3 Stresses in the soil due to a line load

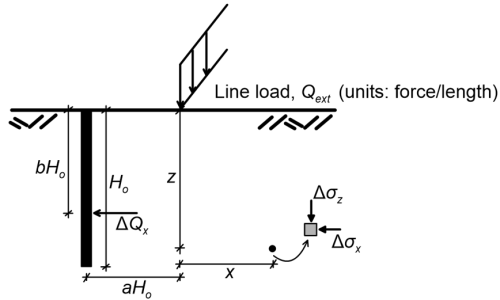
Loading transferred to the soil from e.g., a rail track of limited width (Figure 3.6) can be modelled as an “infinitely long” line load acting on the surface of a homogeneous elastic half-space. As plane-strain symmetry conditions apply, additional soil stresses due to the application of a line load can be calculated as:

Diagram illustrating a line load acting on the surface of a half-space, resulting in vertical Δσ_z and horizontal stresses in soil Δσ_x at depth z and distance x from the load, as well as a horizontal force ΔQ_x on a nearby retaining wall of length Ho.
Figure 3.6. Stresses due to line load acting on the surface of a homogeneous elastic half-space (right), and in the vicinity of a retaining wall (left). Line loads carry units of force per running meter.

(3.5) \Delta {\sigma _z} = \dfrac{{2{Q_{ext}}{z^3}}}{{\pi {{\left( {{x^2} + {z^2}} \right)}^2}}}

(3.6) \Delta {\sigma _x} = \dfrac{{2{Q_{ext}}{x^2}z}}{{\pi {{\left( {{x^2} + {z^2}} \right)}^2}}}

(3.7) \Delta {\tau _{zx}} = \dfrac{{2{Q_{ext}}x{z^2}}}{{\pi {{\left( {{x^2} + {z^2}} \right)}^2}}}

The stress increment components and the vertical z and horizontal x distance from the line load considered in Eqs. 3.5 to 3.7 are defined in Figure 3.6.

In the special case where the line load is acting near the crest of a retaining wall, the horizontal stress distribution along the wall height can be determined as function of the height of the wall Ho (Figure 3.6):

(3.8) \Delta {\sigma _x} = \dfrac{{4{Q_{ext}}{a^2}b}}{{\pi {H_o}{{\left( {{a^2} + {b^2}} \right)}^2}}}

and the resultant horizontal force per running meter of the wall is equal to (Figure 3.6):

(3.9) \Delta {Q_x} = \dfrac{{2{Q_{ext}}}}{{\pi \left( {{a^2} + 1} \right)}}

Note that Eq. 3.8 yields identical results to Eq. 3.5, the only difference between these expressions is that in Eq. 3.8 the coordinates x and z as expressed as function of Ho.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book