3.2 Stresses in the soil due to a point load
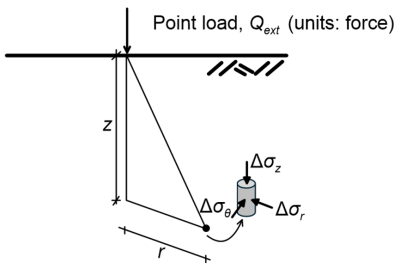
Load transferred to the soil from e.g., the foundation of an electric power pole can be simulated as a point load Qext acting on the surface of a homogeneous elastic half-space (Figure 3.5). As both load and geometry are axisymmetric, additional soil stresses due to the application of the load can be calculated as:
(3.1) ![Rendered by QuickLaTeX.com \Delta {\sigma _z} = \dfrac{{3{Q_{ext}}}}{{2\pi {z^2}{{\left[ {1 + {{\left( {\dfrac{r}{z}} \right)}^2}} \right]}^{\tfrac{5}{2}}}}}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-c0878fbc455c1917ed78f4126cc5d8cf_l3.png)
(3.2) 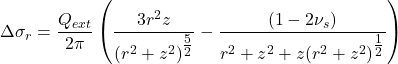
(3.3) 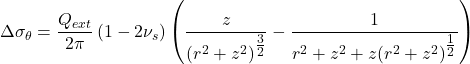
(3.4) 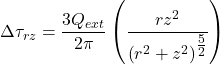
The above expressions provide the stress increments Δσ due to the application of the point load, which should be added to existing geostatic stresses to find the total stress in the soil. In Eqs. 3.1 to 3.4 vs is the Poisson ratio of the soil, while the corresponding stress components Δσz, Δσr, Δσθ and Δτrz and the vertical z and radial r distance from the point load are defined in Figure 3.5.

