"

3.9 Additional problems

3.9.1

You are called to verify Saint-Venant’s principle on the difference between the effects of two dissimilar yet statically equivalent loadings becoming negligible at sufficiently large distances from the loading. For that, you should calculate the vertical stress increment Δσz below the axis of an infinite strip pressure of magnitude qext = 100 kPa and width B = 2 m, and compare it with the corresponding value of Δσz due to a statically equivalent line load, Qext. Try the comparison at depths z = 1 m, z = 3 m and z= 9 m from the ground surface.

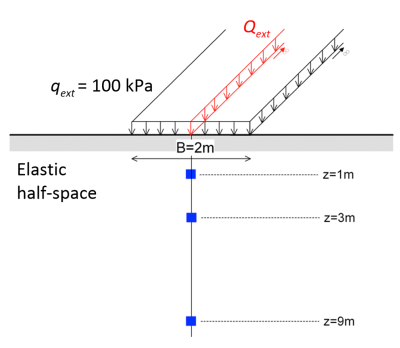
Diagram showing an external pressure q_ext=100 kPa, and a line load Q_ext acting on the surface of an elastic half-space. Three different points at depth z= 1m, 3m, and 9m underneath the axis of the line load are identified.
Additional problem 3.9.1. Problem description and input parameters.

Answer:

Additional problem 3.9.1 Answers
z (m) Δσz (strip pressure, kPa) Δσz (line load, kPa) Difference (Δσz,line-Δσz,strip)/Δσz,line (%)
1.00 81.83 127.32 55.59
3.00 39.58 42.44 7.22
9.00 14.03 14.15 0.82

3.9.2

A line load of magnitude Qext = 100 kN/m is applied at 2 m from the crest of a 4 m-deep excavation, which is supported by a flexible retaining wall e.g., a sheet pile wall. Calculate the horizontal stress Δσx due to the external load acting on the wall at z = 1 m and z = 3 m from the top of the wall. Calculate the stresses again, considering this time a rigid retaining wall e.g., a basement reinforced concrete wall.

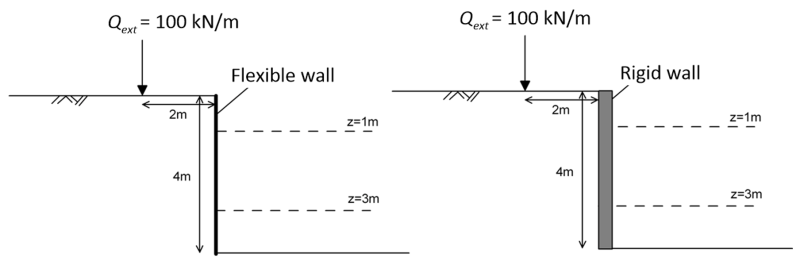
The figure on the left shows an excavation of depth 4m supported by a flexible wall. A line load 100kN/m is acting at 2m from the crest of the excavation. The figure on the right shows an excavation of depth 4m supported by a rigid wall. A line load 100kN/m is acting at 2m from the crest of the excavation. Depths z=1 and z=3m, measured from the crest of the two excavations are identified.
Additional problem 3.9.2. Problem description and input parameters.

Answer:

Additional problem 3.9.2 Answers
z(m) Δσx (flexible wall, kPa) Δσx (rigid wall, kPa)
1.00 10.19 20.38
3.00 4.52 9.04

3.9.3

Two alternative routes are examined for a sewage pipeline, passing below locations A and B. You are the designers of the pipeline. Which one would you prefer, and why? Justify your answer.

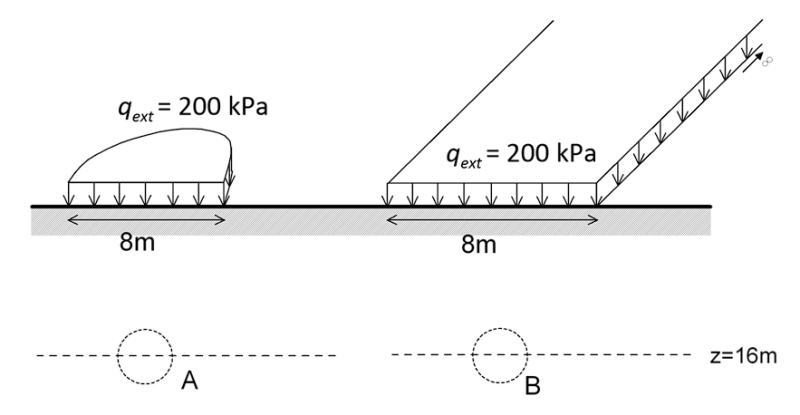
Schematic showing a pipe underneath a circular pressure 200 kPa (left) and a strip pressure 200 KPa (right). The depth of the pipe is 16 m in both cases.
Additional problem 3.9.3. Problem description and input parameters.

Answer:

Location A.

3.9.4

Calculate the vertical stress below the axis of the embankment shown below, at a depth z = 10 m.

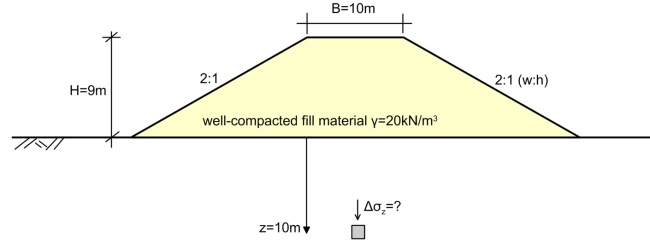
Schematic illustrating a well-compacted fill of trapezoidal section with height 9m and crest with 10m. The inclination of the slopes is 2 horiz : 1 vert. A soil element is identified at the middle of the embankment, at depth 10m from the ground surface, and the additional vertical stress Δσ_z at that element is requested.
Additional problem 3.9.4. Problem description and input parameters.

Answer:

Δσz = 136 kPa

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book