3.5 Stresses in the soil due to a circular pressure
Stresses transferred to the soil from a circular footing such as e.g., the foundation of a tank or a silo, can be modelled as a circular pressure acting on the surface of a homogeneous elastic half-space (Figure 3.8). Considering a uniform vertical pressure, where both loading and geometry are axisymmetric, stress increments due to the application of the pressure qext below the axis of the applied pressure can be calculated as:
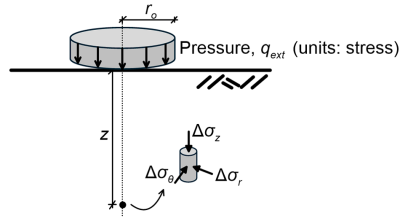
(3.13) ![\Delta {\sigma _z} = {q_{ext}}\left[ {1 - {{\left( {\dfrac{1}{{1 + {{\left( {\dfrac{{{r_o}}}{z}} \right)}^2}}}} \right)}^{\tfrac{3}{2}}}} \right]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-c57090a90ca2ef08a1ced34b64961275_l3.png "Rendered by QuickLaTeX.com")
(3.14) ![\Delta {\sigma _r} = \Delta {\sigma _\theta } = \dfrac{{{q_{ext}}}}{2}\left[ {\left( {1 + 2{\nu _s}} \right) - \dfrac{{4\left( {1 + \nu } \right)}}{{{{\left[ {1 + {{\left( {\dfrac{{{r_o}}}{z}} \right)}^2}} \right]}^{\tfrac{1}{2}}}}} + \dfrac{1}{{{{\left[ {1 + {{\left( {\dfrac{{{r_o}}}{z}} \right)}^2}} \right]}^{\tfrac{3}{2}}}}}} \right]](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-3dbdff231418ae764a5902570891fd64_l3.png "Rendered by QuickLaTeX.com")
In Eqs. 3.13 and 3.14 vs is the soil’s Poisson ratio, ro is the radius of the area where pressure is applied, while the corresponding stress increment components Δσz, Δσr and Δσθ are defined in Figure 3.8.
