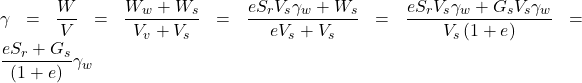"

Appendix A: Phase relationships

Generally, soil is a three-phase material consisting of air, water and solids. Of course, fully saturated or dry soils are two-phase materials, but these are merely special cases. The relative volume or mass of each one of these phases will affect soil behaviour as continuum, and this has led to the definition of a series of quantities and relationships (phase relationships) that are correlated to the physical properties of soils. These quantities are defined in the following.

The water content w (often referred to as moisture content) is the ratio of the weight of the water phase Ww over the weight of the solids Ws. By definition, the water content can attain values from zero up to higher than one.

(A.1) w = \dfrac{{{W_w}}}{{{W_s}}}

It is reminded here that weight W is correlated to mass M as: W = Mg, where g is the gravity coefficient.

The degree of saturation Sr is the ratio of the volume of the water phase Vw over the total volume of voids Vv. By definition, the degree of saturation can attain values from zero (dry soil) up to one (fully saturated soil).

(A.2) {S_r} = \dfrac{{{V_w}}}{{{V_v}}}

The void ratio e is the ratio of the volume of voids Vv to the volume of solids Vs and can again attain values higher than one.

(A.3) e = \dfrac{{{V_v}}}{{{V_s}}}

The porosity n, defined as the volume of voids per unit volume of soil V is often used instead of the void ratio, although the two quantities as directly related as:

(A.4) n = \dfrac{{{V_v}}}{V} = \dfrac{{{V_v}}}{{{V_v} + {V_s}}} = \dfrac{e}{{1 + e}}

or

(A.5) e = \dfrac{n}{{1 - n}}

A third quantity used to quantify the relative volume of voids is the specific volume v, which is defined as the unit volume of soil V over the volume of solids Vs:

(A.6) v = \dfrac{V}{{{V_s}}} = \dfrac{{{V_v} + {V_s}}}{{{V_s}}} = 1 + e   

The specific gravity of soil particles Gs is defined as the weight of the solids over the weight of a quantity water of the same volume:

(A.7) {G_s} = \dfrac{{{W_s}}}{{{V_s}{\gamma _w}}}

where γw = Mw/Vw is the unit weight of water, γw  ≈ 10 kN/m3. Specific gravity depends on soil mineralogy, for silica-based soils it is Gs ≈ 2.65.

In the light of Eqs. A.7 and A.3 and considering that Mw = Vwγw we can re-write Eq. A.2 that provides the degree of saturation as:

(A.8) 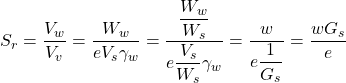{S_r} = \dfrac{{{V_w}}}{{{V_v}}} = \dfrac{{{W_w}}}{{e{V_s}{\gamma _w}}} = \dfrac{{\dfrac{{{W_w}}}{{{W_s}}}}}{{e\dfrac{{{V_s}}}{{{W_s}}}{\gamma _w}}} = \dfrac{w}{{e\dfrac{1}{{{G_s}}}}} = \dfrac{{w{G_s}}}{e}

So, for a fully saturated soil (Sr = 1) the water content and the void ratio are directly correlated as:

(A.9) e = w{G_s}

The unit weight, or more properly the bulk unit weight, γ of soil is its weight W per unit volume V. The terms unit weight and bulk unit weight are often used interchangeably, and are applicable to soils featuring any degree of saturation Sr.

(A.10) \gamma = \dfrac{W}{V}

We can further write:

(A.11) \gamma = \dfrac{W}{V} = \left( {\dfrac{{{G_s} + {S_r}e}}{{1 + e}}} \right){\gamma _w} = \dfrac{{{G_s}\left( {1 + w} \right)}}{{1 + e}}{\gamma _w}

Observe from Eq. A.11 that the unit weight of soil depends on its degree of saturation Sr. In the special case where the soil is saturated (Sr = 1) then Eq. A.11 becomes:

(A.12) {\gamma _{sat}} = \left( {\dfrac{{{G_s} + e}}{{1 + e}}} \right){\gamma _w}

where γsat is the saturated unit weight. On the other hand, in the special case where the soil is dry (Sr = 0) it is:

(A.13) {\gamma _d} = \left( {\dfrac{{{G_s}}}{{1 + e}}} \right){\gamma _w}

where γd is the dry unit weight. A correlation between the dry unit weight and the bulk unit weight can be found if we substitute Eq. A.11 into Eq. A.13 as:

(A.14) \gamma = \left( {1 + w} \right){\gamma _d}

The effective or buoyant unit weight of saturated soil submerged in water is defined as:

(A.15) \gamma ' = {\gamma _{sat}} - {\gamma _w} = \left( {\dfrac{{{G_s} - 1}}{{1 + e}}} \right){\gamma _w}

Often, instead of the unit weight of soil, we use the mass density ρ equal to the ratio of the soil mass M per unit volume V:

(A.16) \rho = \dfrac{M}{V} = \dfrac{W}{{Vg}} = \dfrac{\gamma }{g}

where g again is the gravity coefficient. In a similar way we can define the saturated mass density ρsat :

(A.17) {\rho _{sat}} = \left( {\dfrac{{{G_s} + e}}{{1 + e}}} \right){\rho _w}

where ρw  ≈ 10 Mg/m3 is the mass density of water. Similarly, the dry mass density ρdry is:

(A.18) {\rho _d} = \left( {\dfrac{{{G_s}}}{{1 + e}}} \right){\rho _w}

Note: Eq. A.11 is derived as:

\gamma = \dfrac{W}{V} = \dfrac{{{W_w} + {W_s}}}{{{V_v} + {V_s}}} = \dfrac{{e{S_r}{V_s}{\gamma _w} + {W_s}}}{{e{V_s} + {V_s}}} = \dfrac{{e{S_r}{V_s}{\gamma _w} + {G_s}{V_s}{\gamma _w}}}{{{V_s}\left( {1 + e} \right)}} = \dfrac{{e{S_r} + {G_s}}}{{\left( {1 + e} \right)}}{\gamma _w}

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book