"

Example 6.12

Calculation of the ultimate geotechnical strength and of the pile head deflection of a laterally loaded pile driven in undrained soil

A steel pipe pile of external diameter Dext = 0.4 m and internal diameter Dint = 0.39 m is driven through a layer of uniform, stiff overconsolidated clay with undrained shear strength Su = 100 kPa. The design yield strength of the pile’s steel material is σy = 450 MPa, and the Young’s modulus of the steel material is Ep = 210 GPa. The necessary pile length to safely carry the vertical load is L = 10 m. Assuming the pile is connected with a rigid cap (fixed-head), determine the collapse lateral load Hf, and the deflection of the pile’s head at a serviceability load equal to half the collapse lateral load Hw = Hf/2.

Answer:

Both long and short pile failure must be considered to determine the collapse lateral load, according also to AS2159. To do that, we must first estimate the yield moment My of the pile’s section, which is the maximum moment that the pile’s section can carry before a plastic hinge is formed. For a hollow pipe pile and homogeneous material, the plastic moment is estimated from Table 6.14 as:

{M_y} = \left( {\dfrac{{D_{ext}^3 - D_{{\mathop{\rm int}} }^3}}{6}} \right){\sigma _y} = \left( {\dfrac{{{{0.4}^3} - {{0.39}^3}}}{6}} \right)450000 = 351{\rm{ \:kNm}}

We will start by applying the short-pile equations. If the resulting maximum pile moment Mmax is higher than the yield moment (351 kNm), the long-pile equations should be used instead, as they will result in a lower collapse load. For the case herein, the collapse lateral load considering short-pile failure is (Eq. 6.106):

{H_f} = 9{S_u}{D_{ext}}\left( {L - 1.5{D_{ext}}} \right) = 9 \times 100 \times 0.4 \times \left( {10 - 1.5 \times 0.4} \right) = 3384{\rm{ \:kN}}

and the maximum moment corresponding the ultimate lateral load (Eq. 6.107):

{M_{\max }} = 4.5{S_u}{D_{ext}}\left( {{L^2} - 2.25D_{ext}^2} \right) = 4.5 \times 100 \times 0.4 \times \left( {{{10}^2} - 2.25 \times {{0.4}^2}} \right) = 17935{\rm{ \:kNm}} > {M_y}

It is thus clear that the pile will develop a plastic hinge before a short-pile failure mode fully develops, and the long-pile equations must be used instead. The collapse later load considering long-pile failure is given by substituting Eq. 6.104 into Eq. 6.109 as:

{H_f} = \dfrac{{2{M_y}}}{{\left( {1.5{D_{ext}} + 0.5\dfrac{{{H_f}}}{{9{S_u}{D_{ext}}}}} \right)}} = \dfrac{{2 \times 351}}{{1.5 \times 0.4 + 0.5\left( {\dfrac{{{H_f}}}{{9 \times 100 \times 0.4}}} \right)}}\

{H_f} = 527.03{\rm{ \:kN}}

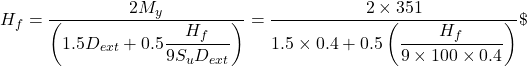
However, we have to further check whether the collapse lateral load that will result while considering intermediate pile failure is not lower than 527.03 kN. Employing Eq. 6.110 and substituting f from Eq. 6.104 yields:

{H_f} = \dfrac{{{M_y} + 2.25{S_u}{D_{ext}}{{\left( {L - 1.5D - \dfrac{{{H_f}}}{{9{S_u}{D_{ext}}}}} \right)}^2}}}{{\left( {1.5D + 0.5\dfrac{{{H_f}}}{{9{S_u}{D_{ext}}}}} \right)}}

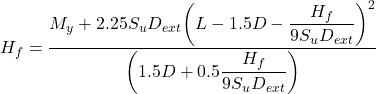
The above equation can be solved for Hf, and results in Ηf = 1333.6 kN > 527.03 kN, which means that long pile failure is critical. Indeed, if we substitute Hf in Eq. 6.111 for the bending moment that will develop at a depth 1.5D+f:

{M_{\max }} = 2.25{S_u}{D_{ext}}{\left( {L - 1.5{D_{ext}} - \dfrac{{{H_f}}}{{9{S_u}{D_{ext}}}}} \right)^2} = 2.25 \times 100 \times 0.4 \times {\left( {10 - 1.5 \times 0.4 - \dfrac{{527.03}}{{9 \times 100 \times 0.4}}} \right)^2} = 5668{\rm{ \:kNm}} > {M_y}

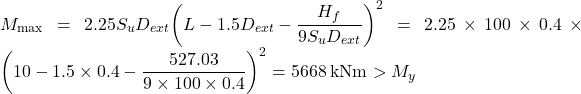
which implies that two plastic hinges will be formed along the pile.

The pile head displacement for the working lateral load Hw = Hf/2 = 263.5 kN will be estimated while calculating the modulus of subgrade reaction according to Davidson (1972) as:

{K_h} = 67\dfrac{{{S_u}}}{{{D_{ext}}}} = 16750{\rm{ \:kN/}}{{\rm{m}}^3}

In order to use Figure 6.101, we must first estimate the factor β from Eq. 6.115:

\beta = {\left( {\dfrac{{{K_h}{D_{ext}}}}{{4{E_p}{I_p}}}} \right)^{0.25}}

where:

{I_p} = \pi \left( {\dfrac{{D_{ext}^4 - D_{{\mathop{\rm int}} }^4}}{{64}}} \right) = 0.000121{\rm{ }}{{\rm{\:m}}^4}

is the moment of inertia of the hollow pile’s cross-section, and

\beta = {\left( {\dfrac{{16750\times 0.4}}{{4 \times 210 \times {{10}^6} \times 1.21 \times {{10}^{ - 4}}}}} \right)^{0.25}} = 0.50

Considering the curve for fixed-head piles of Figure 6.101 and βL = 5, we obtain:

y(0) = 5\left( {\dfrac{{{H_w}}}{{{K_h}{D_{ext}}L}}} \right) = 5\left( {\dfrac{{263.5}}{{16750 \times 0.4 \times 10}}} \right) = 0.019{\rm{ m}}

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book