"

Example 6.9

Calculation of settlement of an end-bearing pile in layered soil

Calculate the immediate settlement of the driven solid concrete pile shown in the Figure below, using i) the method of Poulos and Davis (1991) for end-bearing piles in uniform soil underlaid by rigid bedrock (claystone) and ii) the method of Zheng et al. (2023) for end-bearing piles in two-layered soil underlaid by rigid bedrock. Repeat the calculation, this time considering that instead of rigid claystone, the bedrock consists of hard alluvial clay with Eb = 55 MPa.

Schematic of an end-bearing concrete pile which toe is founded on incompressible claystone or hard alluvial clay with Eb = 55 MPa. The pile is subjected to an axial compressive force Qw = 1 MN. The pile's length is L = 10 m and the pile's diameter is D = 0.5 m. The pile is driven through layered soil. The top stiff clay layer (overconsolidated crust) has thickness h1 = 5 m, Young's modulus Eu = 10 MPa and Poisson's ratio vu = 0.5. The bottom soft clay layer (estuarine deposits) has thickness h2 = 5 m, Young's modulus Eu = 1 MPa and Poisson's ratio vu = 0.5. The Young's modulus of the pile's material is Ep = 25 GPa.
Example 6.9. Problem description and input parameters.

1. Calculation of settlement according to Poulos and Davis (1991) for Eb = inf:

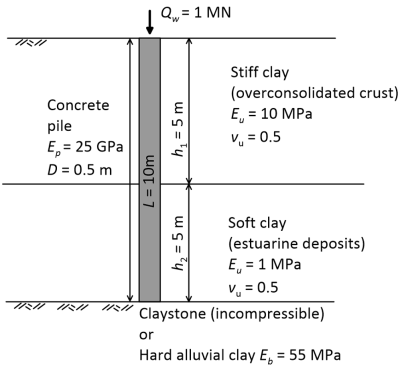
We estimate the pile head stiffness factor Ib from Figure 6.71 using a weighted average soil modulus from Eq. 6.94 equal to Es = 5.5 MPa. For Kp = Ep/Es (solid pile) = 25,000/5.5 = 4,545 and L/D = 20 it is Ib ≈ 0.98 (see Figure below).

A graph showing the relationship between Ib and Kp in pile mechanics, with labeled curves and an end-bearing pile illustration.
Example 6.9. Calculation of Ib.

Therefore settlement of the end-bearing pile is equal to:

\dfrac{{{E_p}{A_p}{\rho _e}}}{{{Q_w}L}} = {I_b} = 0.98

{\rho _e} = 0.98 \times \dfrac{{1000 \times 10}}{{25000000 \times \left( {\dfrac{{\pi {{0.5}^2}}}{4}} \right)}} = 1.99{\rm{\: mm}}

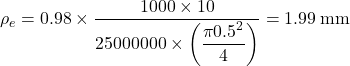
2. Calculation of settlement according to Zheng et al. (2024) for Eb = inf:

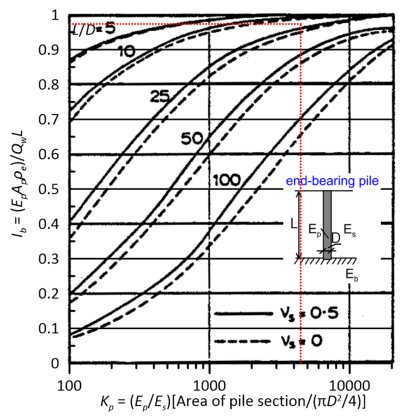
In lack of charts for soil Poisson’s ratio vs = 0.5, we will use the chart of Figure 6.74 to estimate the pile head stiffness Qw/EpDρe. Since here Ep/Es2 = 25,000 we will use the chart for the nearest Kp value of Kp= Ep/Es2 (solid pile) = 5,000 and Es1/Es2 = 10, L/D = 20. As shown below, we obtain Qw/EpDρe ≈ 0.048.

Chart showing the variation of pile head stiffness Qw/(EsDρe) with pile slenderness L/D when Ep/Es2 = 5000, vs = 0.3, h1=h2 and Es1>Es2. The chart contains multiple curves, each one for different Es1/Es2 values. For L/D = 20 and Es1/Es2 = 10 its is found that the pile head stiffness is approximately 0.048.
Example 6.9. Calculation of pile head stiffness.

Therefore pile settlement is estimated to be:

{\rho _e} = \dfrac{{{Q_w}}}{{{E_p}D \times 0.048}} = \dfrac{{1000}}{{25000000 \times 0.5 \times 0.048}} = 1.66{\rm{ \:mm}}

This settlement value is lower to that computed with the method of Poulos and Davis, which requires using a weighted average soil modulus if the pile is driven in layered soil.

3. Calculation of settlement for hard alluvial clay bedrock (Eb = 55 MPa) :

We first consider the pile as friction pile, and obtain the factor Is from Figure 6.66. For Kp = Ep/Es (solid pile) = 25,000/5.5 = 4,545 and L/D = 20 it is Is ≈ 0.09.

Thus, from Eq. 6.95 it is:

{\rho _{e,friction}} = \dfrac{{{Q_w}}}{{{E_s}D}}{I_s} = \dfrac{{1000}}{{5500 \times 0.5}}0.09 = 32.7{\rm{ \:mm}}

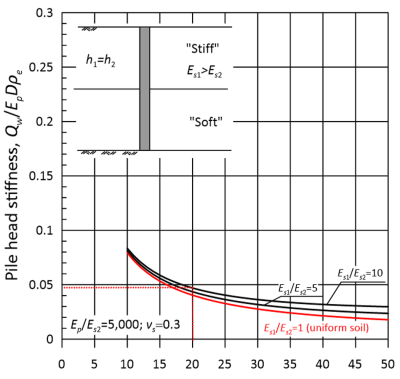
We can now refer to Figure 6.72 and estimate the settlement of the end-bearing pile, as function of ρe,friction while considering pile slenderness L/D = 20 and Eb/Es = 55/5.5 = 10. Note that the particular figure presents results for Kp = 1000, therefore will provide an upper bound of settlement as here Kp = 4,545.

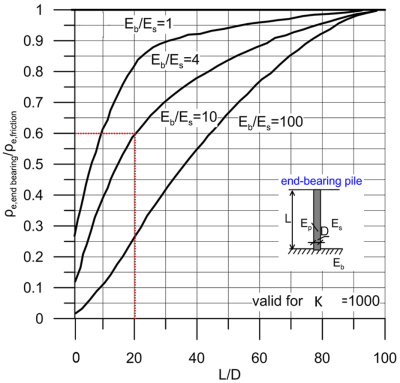
Graph showing the variation of (ρe,end bearing/ρe.friction) with L/D. Four curves for different Eb/Es values are shown. The characteristics of an end bearing pile are shown in an inset figure: The length of the pile is denoted with L, its diameter is denoted with D, the Young's modulus of the pile's material is denoted with Ep, the Young's modulus of soil is denoted with Es and the Young's modulus of the end bearing stratum is denoted with Eb. It is noted that this chart is valid for K = 1000. For L/D = 20 and Eb/Es = 10 it is found that (ρe,end bearing/ρe.friction)=0.6.
Example 6.9. Calculation of ρe,end bearing/ρe,friction.

The above figure suggests that ρe,friction/ρe,end bearing = 0.6, therefore  ρe = 0.6 × 32.7 = 19.6 mm.

It is clear from the above that: i) Considering a weighted average modulus may result in overestimating settlement when the surficial layer (crust) is stiffer than the bottom layer (soft soil), and ii) Assuming that the bedrock is incompressible can result in significantly underestimating settlement of relatively short piles (low L/D values), when the ratio of Young’s modulus of the bedrock over the Young’s modulus of the soil layer is Eb/Es = 10, or less.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book