"

Example 6.8

Calculation of settlement of a friction pile in homogeneous soil

Calculate the immediate settlement of the driven solid concrete pile shown in the figure below, using i) the method of Poulos (1998) for friction piles in infinitely deep soil and ii) the method of Zheng et al. (2023) for friction piles in a soil layer of finite thickness.

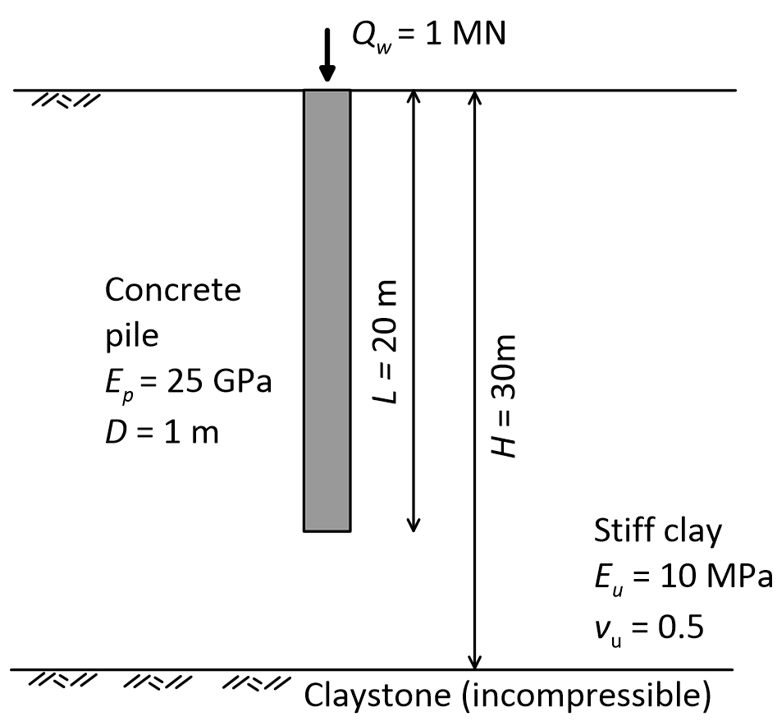
Schematic of a friction concrete pile. The pile is subjected to an axial compressive force Qw. The pile's length is L and the pile's diameter is D. The soil layer in which the pile is driven has thickness H (H>L) and features Young's modulus Es and Poisson's ratio vs. The soil layer is underlaid by incompressible rock.
Example 6.8. Problem description and input parameters.

Answer:

1. Calculation of settlement according to Poulos (1998):

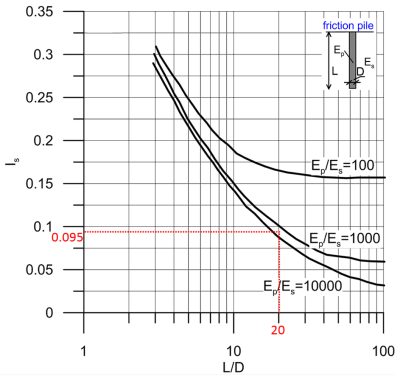
First, we estimate the pile head stiffness factor Is from Figure 6.66. For Kp = Ep/Es (solid pile) = 25,000/10 = 2500 and L/D = 20 it is Is ≈ 0.095 (see Figure below).

Graph showing the variation of the factor Is with pile slenderness L/D. Three curves for different Ep/Es values are shown. The characteristics of a friction pile are shown in an inset figure: The length of the pile is denoted with L, its diameter is denoted with D, the Young's modulus of the pile's material is denoted with Ep and the Young's modulus of soil is denoted with Es. A line is drawn from L/D = 20 and the midpoint between the Ep/Es = 10000 and Ep/Es = 1000 curves is found at Is = 0.095.
Example 6.8. Calculation of Is.

Thus, from Eq. 6.92 it is:

{\rho _e} = \dfrac{{{Q_w}}}{{{E_s}D}}{I_s} = \dfrac{{1000}}{{10000 \times 1}}0.095 = 9.5{\rm{ \:mm}}

2. Calculation of settlement according to Zheng et al. (2023):

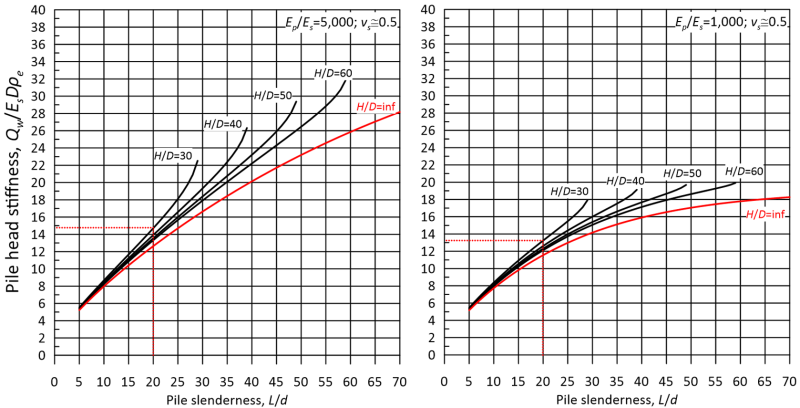
We estimate the pile head stiffness from Figure 6.70, which presents results for vs = 0.5. For Kp = Ep/Es (solid pile) = 5000, H/D = 30 and L/D = 20 it is Qw/EsDρe ≈ 14.8 while for K = Ep/Es = 1000, H/D = 30 and L/D = 20 it is Qw/EsDρe ≈ 13.2  (see Figure below).

Two charts showing the variation of pile head stiffness Qw/(EsDρe) with pile slenderness L/D. The figure on the left corresponds to Ep/Es = 5000 and vs = 0.5. The figure on the top right corresponds to Ep/Es = 1000 and vs = 0.5. Each chart contains multiple curves, for different H/D values ranging from H/D=30 to H/D=infinity. From the figure on the left for L/D = 20 it is found that the stiffness is approximately 14.8, and from the figure on the right for L/D = 20 it is found that the stiffness is approximately 13.2.
Example 6.8. Calculation of pile head stiffness.

Using linear interpolation we can obtain:

\dfrac{{\dfrac{{{Q_w}}}{{{E_s}D{\rho _e}}} - 13.2}}{{{K_p} - 1000}} = \dfrac{{14.8 - 13.2}}{{5000 - 1000}}

\dfrac{{\dfrac{{{Q_w}}}{{{E_s}D{\rho _e}}} - 13.2}}{{2500 - 1000}} = 0.0004

\dfrac{{{Q_w}}}{{{E_s}D{\rho _e}}} = 13.8

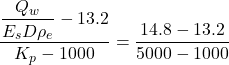
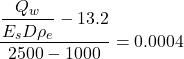
Therefore the settlement ρe is:

{\rho _e} = \dfrac{{1000}}{{13.8 \times 10000 \times 1}} = 7.2{\rm{ \:mm}}

i.e., as expected, lower than that calculated using the method of Poulos because the method of Zheng et al. accounts for the actual thickness of the soil layer.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book