"

Example 4.5

Estimation of 2-D primary consolidation settlement

Calculate the primary consolidation settlement below the axis of symmetry of the circular footing shown below.

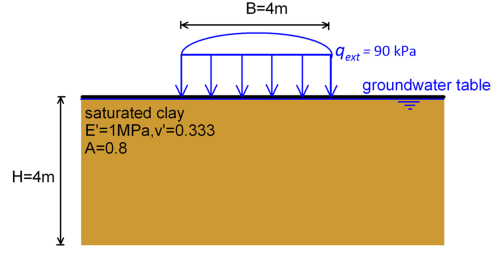
Schematic of a circular pressure of diameter 4m and magnitude 90 kPa, acting on the surface of a saturated clay layer of thickness H = 4 m. The properties of the saturated clay are E' = 1 MPa, v' = 0.333, A = 0.8. The groundwater table is found at the ground surface.
Example 4.5. Problem description and input parameters.

The diameter of the footing B = 4 m is comparable to the thickness of the compressible layer H = 4 m, B < (3 to 4)H so we have to take into account the development of lateral strains during the estimation of primary consolidation settlement.

For simplicity: a) we will consider the compressible layer as an elastic half-space for the calculation of stresses, as the additional effective stress due to the pressure from the footing Δσ′z cannot be assumed to remain constant with depth, and b) we will not divide the compressible clay layer into sublayers. The effect of the former assumption on settlement estimates is discussed in the next Chapter.

The expression for estimating vertical stresses below the axis of symmetry of a circular pressure is provided in Chapter 3.5:

\Delta {\sigma _z} = {q_{ext}}\left[ {1 - {{\left( {\dfrac{1}{{1 + {{\left( {\dfrac{B}{{2z}}} \right)}^2}}}} \right)}^{\frac{3}{2}}}} \right]

where B/2 is the footing radius. At the middle of the compressible layer z = 2 m:

\Delta {\sigma _z} = 90\left[ {1 - {{\left( {\dfrac{1}{{1 + {{\left( {\dfrac{2}{2}} \right)}^2}}}} \right)}^{\frac{3}{2}}}} \right] = 58.18{\rm{ \:kPa}}

At the end of consolidation Δσ′z = Δσz. For H/B = 1, A = 0.8 and circular footing geometry, Figure 4.32 provides a settlement correction factor μSB ≈ 0.87. Furthermore, the coefficient of volume compressibility is calculated from Eq. 4.23 as:

{m_v} = \dfrac{{\left( {1 + v'} \right)\left( {1 - 2v'} \right)}}{{\left( {1 - v'} \right)E'}} = \dfrac{2}{{3E'}} = 6.666 \times {10^{ - 4}}\dfrac{{{{\rm{m}}^{\rm{2}}}}}{{{\rm{kN}}}}

Substituting in Eq. 4.37 results in a primary consolidation settlement due to the pressure applied on the footing equal to:

{\rho _{pc}} = {\mu _{SB}}{m_v}\Delta {\sigma '_z}H = 0.87 \times 6.666 \times {10^{ - 4}} \times 58.18 \times 4 = 0.13{\rm{\:m}}

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book