"

Example 4.3

Estimation of 1-D primary consolidation settlement assuming linear elastic soil response

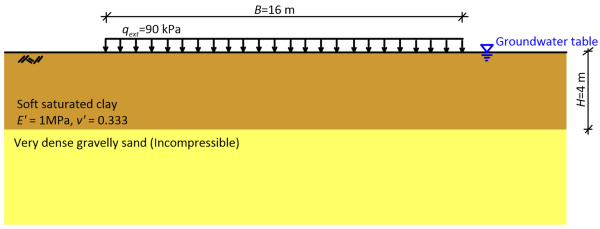
Calculate the primary consolidation settlement due to the strip pressure of the figure, assuming linear elastic soil response.

Graph showing a pressure q_ext = 90 kPa of width B = 16 m applied on the surface of a soft saturated clay layer of thickness H = 4 m. The properties of the clay layer are E' = 1 MPa and v' = 0.333. The clay layer is underlaid by very dense gravelly sand, denoted as incompressible. The water table is at the ground surface.
Example 4.3. Problem description and input parameters.

Answer:

The width of the loaded area B = 16 m is large, compared to the thickness of the compressible layer H = 4 m, B > (3 to 4)H so we can effectively assume 1-D consolidation conditions. After excess water pore pressure has dissipated, the additional effective stress Δσ′z due to the application of the external pressure will be equal to the applied pressure i.e., Δσ′z  = qext = 90 kPa. In order to apply Eq. 4.24 to find the final value of consolidation settlement, we have to estimate first the coefficient of volume compressibility from Eq. 4.23 as:

{m_v} = \dfrac{{\left( {1 + v'} \right)\left( {1 - 2v'} \right)}}{{\left( {1 - v'} \right)E'}} = \dfrac{2}{{3E'}} = 6.666 \times {10^{ - 4}}\dfrac{{{{\rm{m}}^{\rm{2}}}}}{{{\rm{kN}}}}

Substituting in Eq. 4.24 yields:

{\rho _{pc}} = {m_v}\Delta {\sigma '_z}H = 6.666 \times {10^{ - 4}}\dfrac{{{{\rm{m}}^{\rm{2}}}}}{{{\rm{kN}}}} \times 90\dfrac{{{\rm{kN}}}}{{{{\rm{m}}^{\rm{2}}}}} \times 4{\rm{\:m}} = 0.24{\rm{ \:m}}

Note that the effective stress in Eq. 4.24 is the additional effective stress due to application of the pressure, not including the geostatic effective stress: settlement is due to changes in effective stress, and is not related to its absolute value when linear elastic response is assumed.

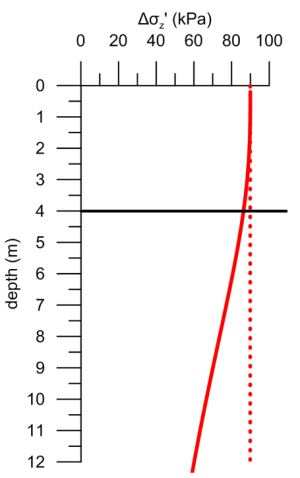
The actual distribution of vertical stresses beneath the axis of the strip pressure is shown below, calculated according to the mentioned in Chapter 3.4. It is clear that assuming the additional stress in the compressible layer to be constant and equal to the applied pressure on the surface Δσ′z = qext = 90 kPa is a quite reasonable assumption, when the thickness of the compressible layer is small compared to the width of the pressure B > (3 to 4)H.

Graph showing the variation of additional vertical effective stress Δσ'_z with depth. It is shown that for depths less than 4 m Δσ'_z is approximately equal to 90 kPa.
Example 4.3. Variation of additional vertical effective stresses with depth.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book