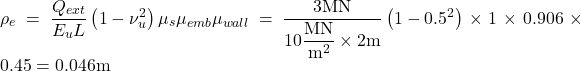"

Example 4.1

Immediate settlement of a footing resting on saturated clay

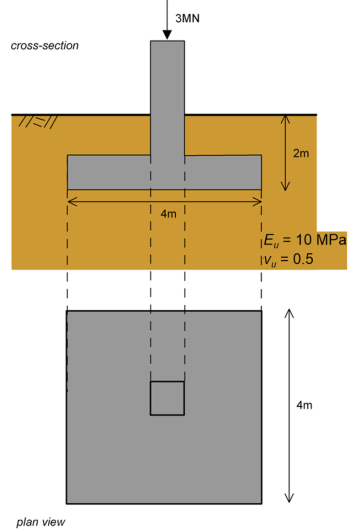
Estimate the immediate settlement of a square 4 m x 4 m footing resting on the surface of a deep homogeneous saturated clay layer, using the methodology described in Section 4.5.4. The working load under serviceability conditions is Qext = 3 MN, the embedment depth is Df = 2 m, and the undrained clay compressibility parameters are Eu = 10 MPa and vu = 0.50.

The top figure presents a cross-section of a rectangular footing with dimensions 4m x 4m, embedded at 2m depth in soil with E_u = 10 MPa and v_u = 0.5. The footing is subjected to a compressive force 3 MN. The bottom figure presents a plan view of the footing, where its length is shown.
Example 4.1. Problem description and input parameters.

Answer:

The area of the rectangular footing is equal to:

Ab=4m x 4m =16 m2

As the half-length of the rectangle side is L = 4 m/2 = 2 m, the factor Ab/4L2 is equal to:

Ab/4L2 = 16/(4×22) = 1

Influence factors μs and μemb accounting for the effect of shape and of footing embedment, respectively, are provided from Eqs. 4.13 and 4.14. As the thickness of the footing is small, the shear resistance that may be mobilised is negligible, thus the influence factor accounting for the effect of wall friction μwall is taken conservatively equal μwall = 1.0.

{\mu _s} = 0.45{\left( {\dfrac{{{A_b}}}{{4{L^2}}}} \right)^{ - 0.38}} = 0.45

{\mu _{emb}} = 1 - 0.04\dfrac{{{D_f}}}{B}\left[ {1 + \dfrac{4}{3}\left( {\dfrac{{{A_b}}}{{4{L^2}}}} \right)} \right] = 1 - 0.04\dfrac{2}{2}\left[ {1 + \dfrac{4}{3} \times 1} \right] = 0.906

The immediate settlement is therefore estimated from Eq. 4.12 as:

{\rho _e} = \dfrac{{{Q_{ext}}}}{{{E_u}L}}\left( {1 - \nu _u^2} \right){\mu _s}{\mu _{emb}}{\mu _{wall}} = \dfrac{{3{\rm{MN}}}}{{10\dfrac{{{\rm{MN}}}}{{{{\rm{m}}^{\rm{2}}}}} \times 2\rm{m}}}\left( {1 - {{0.5}^2}} \right) \times 1 \times 0.906 \times 0.45 = 0.046{\rm{ m}}

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book