Example 3.1

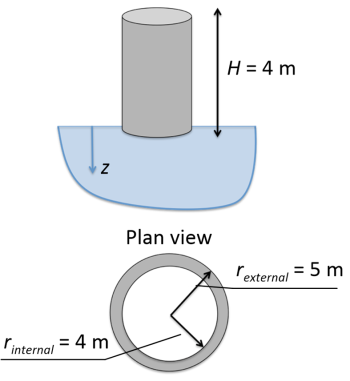
An H = 4 m tall water tank with radius r_external = 5 m is going to be founded on a ring foundation, with the dimensions depicted in the following plan view. Assuming the tank is filled with water, determine the vertical stress due to the weight of the tank below the centre of the foundation, at a depth z = 5 m.

Answer:

First we have to determine the maximum load, Q_ext on the foundation, assuming that the tank is filled with water:

A_tank = πr_external² = 78.54 m²

Q_ext = A × H × y_w = 78.54 m² x 4 m x 10 kN/m³ = 3141 kN where 10 kN/m³ is the unit weight of water.

The area of the ring footing on which the load is applied is:

A_footing= πr_external² – πr_internal2 =78.54 m²-50.26 m² = 28.28 m²

thus the pressure applied on the ring foundation of the tank will be:

q_ext = Q_ext/A_footing = 111 kPa

Employing the principle of superposition discussed in Chapter 3.5, this ring pressure is equivalent, in terms of stresses applied to the soil, to a circular pressure q_ext,1 = 111 kPa on a radius r_external = 5 m, plus a circular pressure q_ext,2 = -111 kPa on a radius r_internal = 4 m (see also Figure 3.14). Negative pressure values correspond to tension. The additional vertical stress in the soil below the axis of symmetry of a circular pressure is provided by Eq. 3.13. At depth z = 5 m, the positive pressure of radius r_external = 5 m will result in a compressive stress:

while the negative pressure of radius r_internal = 4 m in a tensile stress:

The total stress increment due to the loading applied on the ring foundation is found from Eq. 3.21 as: