6.27 Numerical beam-on-nonlinear Winkler spring methods for the analysis of piles subjected to lateral loading
One important drawback of analytical methods, such as that of Broms, is the assumption of uniform soil conditions along the length of the pile. Since piles embedded in uniform soil are probably the exception rather than the rule, numerical methods are now being used extensively in practice for the analysis of piles subjected to lateral loading. Even relatively simple methods, such as the one described in the following, are not limited to uniform conditions (or to pile slenderness larger than the critical, as discussed earlier), and can account for multiple soil layers of varying thickness.
Since lateral loading of a pile is neither an axisymmetric nor a plane strain problem, two-dimensional finite element codes such as PLAXIS 2D cannot be used to model lateral loading of the soil-pile system. Instead, we use beam-on-nonlinear Winkler spring models (see Figure 6.91) where the pile is modelled as one-dimensional beam, and the soil surrounding the pile is replaced with non-linear springs, which provide the reaction on the pile p as function of its deflection y at any depth. External loads are applied on the head of the pile. While closed form solutions cannot be obtained for this problem if the p–y relationship is non-linear, we can use the Finite Element Method to discretise the pile into a finite number of beam elements, and attach spring elements at the beam elements’ nodes. Multilayered soil profiles can model in this way, by considering different p–y relationships for different spring elements. Various commercial codes based on this concept are available in the market, and referring in detail to them is not within the scope of this chapter.
Pivotal to the successful analysis of piles with this method is the selection of appropriate p–y relationships or curves, representative of the soil conditions, of the pile’s geometry and of the type of loading, and the use of realistic input parameters for these expressions. A collection of widely-used mathematical expressions that provide p–y relationships for different soil conditions is presented in the following sections, in the form of step-by-step workflows. Note that the presentation is limited to curves applicable to static, monotonic loading. For cyclic loads featuring a significant number of loading cycles, as the case of offshore platforms subjected to wave loads, the interested reader may refer to Reese and van Impe (2001).
6.27.1 p-y curves for piles embedded in soft clay, in the presence of free water
Step 1:
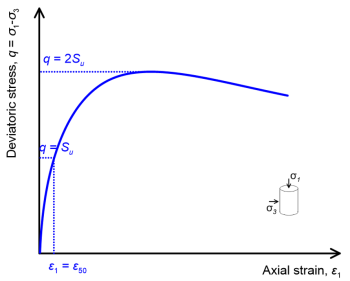
Estimate the undrained shear strength of the clay Su, and the characteristic strain ε50, which is the strain that develops in a clay sample during an undrained triaxial compression test when the deviatoric stress q on the sample becomes equal to q = σ1–σ3 = Su i.e., is half the deviatoric stress at failure (Figure 6.111). If triaxial laboratory tests are not available e.g., when Su is estimated from in situ tests, one can use the typical values listed in Table 6.17. Keep in mind that overconsolidated clays exhibit more brittle behaviour, and will fail at lower strain levels.
| Clay consistency | Undrained shear strength | ε50 |
|---|---|---|
| Soft-to-firm | Su < 50 kPa | 0.020 |
| Firm-to-stiff | 50 < Su < 100 kPa | 0.010 to 0.007 |
| Stiff-to-hard | 100 < Su < 200 kPa | 0.007 to 0.005 |
| Hard-to-very hard | 200 < Su < 400 kPa | 0.004 |
Step 2:
Compute the ultimate soil reaction per unit length of the pile as the minimum of two values:
(6.129) 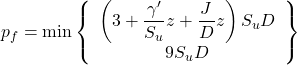
where γ′ = γ – γw is the average submerged unit weight from the ground surface to the depth z where the p-y curve is estimated; J = 0.5 for soft clays or J = 0.25 for medium-to-firm clays (Matlock, 1970). The second term of Eq. 6.129 corresponds to the ultimate soil reaction developing on a smooth rigid pile in undrained perfectly-plastic soil, mentioned earlier in Chapter 6.24.
Step 3:
Compute the deflection of the pile y50 at one-half the ultimate soil reaction p = 0.5pf :
(6.130) ![]()
Step 4:
All the input parameters of the p-y curve have now been determined:
(6.131a) 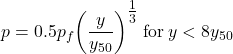
(6.131b) ![]()
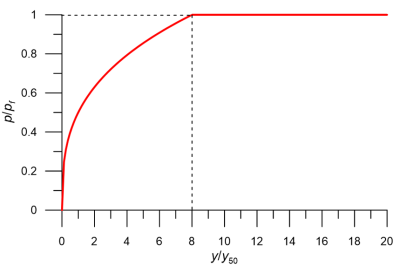
The shape of the p–y curve is depicted in Figure 6.112.
For example, consider a 15-m long pile with diameter D = 0.5 m, driven in soft clay with undrained shear strength increasing with depth, z as Su = 20+z (kPa). The submerged unit weight of the clay is taken equal to γ′ = 6 kN/m3, and it is further assumed that J = 0.5 and ε50 = 0.02. Substituting in Eqs. 6.129 and 6.130 yields:
(6.132) 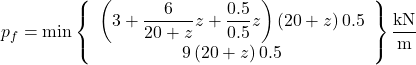
and
(6.133) ![]()
Variation of the ultimate soil reaction per unit length of the pile with depth z is given in Eq. 6.132. Indicatively, for z = 0:
(6.134) ![]()
and the p-y curve is described by the function:
(6.135a) ![]()
(6.135b) ![]()
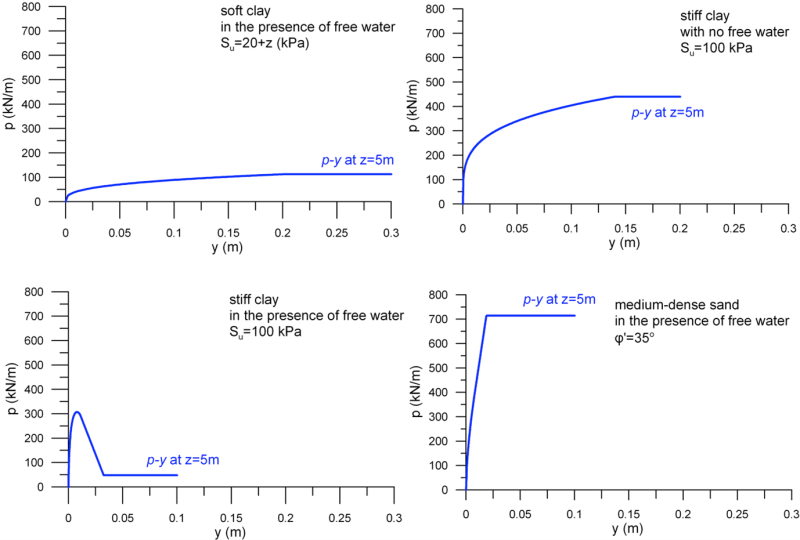
p-y curves for different depths along the length of the pile are illustrated in Figure 6.113. Notice that the ultimate soil reaction pf increases with depth, but not the lateral pile movement necessary to mobilise it, as the latter depends only on the characteristic strain ε50 and on the pile’s diameter.
6.27.2 p-y curves for piles embedded in stiff clay, in the presence of free water
Step 1:
Estimate the undrained shear strength of the clay layer Su at the depth z (measured from the soil surface) where the curve is determined, and the average undrained shear strength over the depth z, Su,aver.
Step 2:
Compute the ultimate soil reaction per unit length of the pile as the minimum of two values:
(6.136) ![]()
where γ′ is the average submerged unit weight from the ground surface to the depth z, defined above. The second term of Eq. 6.136 corresponds to the ultimate soil reaction developing on a rough rigid pile in undrained perfectly-plastic soil, as discussed earlier.
Step 3:
Estimate the factor As from the expressions presented in Figure 6.114, as function of z where the curve is determined. The provided expressions are for static, monotonic loads.
![Graph presenting the variation of the parameter As with dimensionless depth z/D. For z/D < 4 As is calculated as As = 0.11ln[(z/D)+4] > 0.2 and for z/D > 4 As is constant As = 0.6.](https://oercollective.caul.edu.au/app/uploads/sites/143/2025/03/6.114-hr-e1743555161543.png)
Step 4:
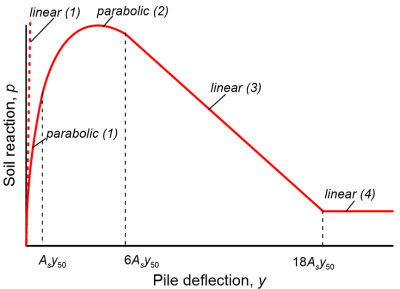
Establish the initial straight-line part of the p-y curve, referred to as linear (1) in Figure 6.115:
(6.137) ![]()
The inclination of its slope ks is provided in the Table 6.18 below.
| Average undrained shear strength to depth z where the p–y curve is estimated | ks (static, kN/m3) |
|---|---|
| Su = 50 to 100 kPa | 135000 |
| Su = 100 to 200 kPa | 270000 |
| Su = 300 to 400 kPa | 540000 |
Step 5:
Compute y50=ε50D. In the absence of undrained triaxial compression laboratory tests, one may use the typical values of ε50 provided in Table 6.17 above.
Step 6:
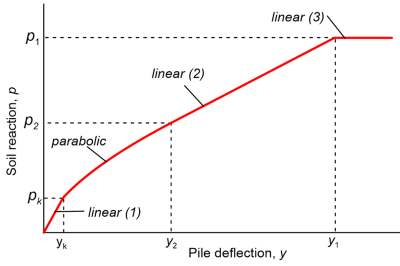
Establish the first parabolic part of the p-y curve, named parabolic(1) in Figure 6.115, using the following Eq. 6.138. It defines the part of the parabolic curve from the intersection with the initial straight line up to a pile lateral deflection equal to Asy50.
(6.138) ![]()
Step 7:
Establish the second parabolic part of the p-y curve, named parabolic(2) in Figure 6.115, using Eq. 6.139. It defines the part of the p-y curve from Asy50 up to pile deflection 6Asy50.
(6.139) ![]()
Step 8:
Establish the next linear part of the p-y curve, named linear(3) in Figure 6.115, according to Eq. 6.140. It defines the softening part of the p-y curve from 6Asy50 up to pile deflection 18Asy50.
(6.140) 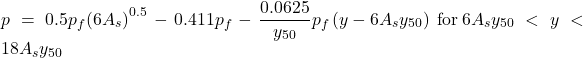
Step 9:
Establish the final linear part of the p-y curve, named linear(4) in Figure 6.115, using Eq. 6.141. This segment corresponds to the residual soil reaction, at large relative soil-pile displacements.
(6.141) ![]()
In many practical cases we can ignore the initial linear part of the curve, as intersection of linear(1) with the parabolic(1) part takes place at very small pile deflection (of the order of 1 mm). This would be the case for a 15-m long pile with diameter D = 0.5 m, driven in stiff clay with assumed constant undrained shear strength Su = 100 kPa and submerged unit weight γ′ = 6 kN/m3. The ultimate soil reaction per unit pile length can be estimated as:
(6.142) ![]()
whereas the factor As is calculated from the formulas depicted in Figure 6.114:
(6.143a) ![]()
(6.143b) ![]()
where z is the depth from the ground surface. From Table 6.17 for undrained shear strength of clay Su = 100 kPa we obtain a characteristic strain ε50 ≈ 0.007 therefore y50 = ε50D = 0.003 m.
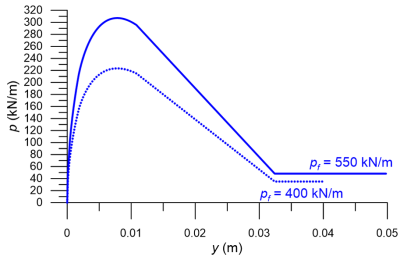
The expressions providing the distinct parts of the p-y curve are presented in Table 6.19.
| Lateral pile deflection, y (m) | Soil reaction, p (kN/m) |
|---|---|
| 0 < y < 0.003As | |
| 0.003As < y < 0.018As | |
| 0.018As < y < 0.054As | |
| y > 0.054As | |
| For z > 2 m it is pf = 550 kN/m and As = 0.6 | |
Notice from Eqs. 6.142 and 6.143 that in this particular case, both the factor As and the ultimate soil resistance do not change for the part of the pile embedded deeper than 2 m, thus the p-y response of the pile for z > 2 m will remain unaltered if the variation of the undrained soil strength with depth is not considered (Figure 6.116). Observe also in Figure 6.116 that the maximum soil reaction acting on the pile is not equal to pf calculated from Eq. 6.136 (see also Eq. 6.139).
6.27.3 p-y curves for piles embedded in stiff clay, when no free water is present
Step 1:
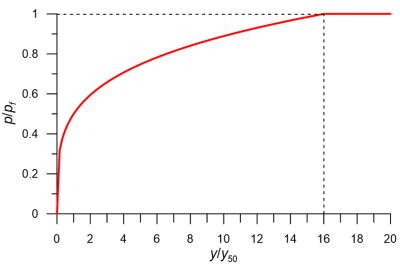
Estimate the undrained shear strength of the clay Su, and the characteristic strain ε50 from laboratory undrained triaxial compression tests. If such tests are not available, ε50 may be estimated from Table 6.17. Keep in mind that higher ε50 values will result in more conservative predictions of pile response to lateral loads.
Step 2:
Compute the ultimate soil resistance per unit length of the pile as the minimum of two values:
(6.144) 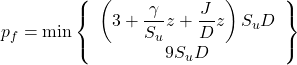
where the factor J takes values J = 0.5 for soft clays and J = 0.25 for medium-to-firm clays.
Step 3:
Compute the deflection y50 at one-half the ultimate soil reaction p = 0.5pf:
(6.145) ![]()
Step 4:
All the input parameters of the p-y curve have now been determined:
(6.146a) ![]()
(6.146b) ![]()
The shape of the p-y curve is depicted in Figure 6.117.
For example, consider a 15-m long pile with diameter D = 0.5 m, driven in stiff clay with undrained shear strength Su = 100 kPa and saturated unit weight γsat = 16 kN/m3. Assuming J = 0.5 and ε50 = 0.007, Eq. 6.144 yields:
(6.147) 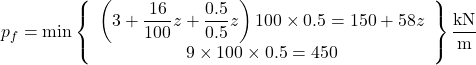
Further, substituting in Eq. 6.145:
(6.148) ![]()
Notice from Eq. 6.147 that the ultimate soil resistance increases up to a depth z = 5.17 m, and remains constant for the part of the pile embedded in larger depths. For shallower depths, the variation of the ultimate soil resistance per unit length of the pile with depth z is given in Eq. 6.147. Indicatively, for z = 0:
(6.149) ![]()
and the p-y curve at z = 0 is described by the function:
(6.150a) ![]()
(6.150b) ![]()
p-y curves along the length of the pile are illustrated in Figure 6.118:
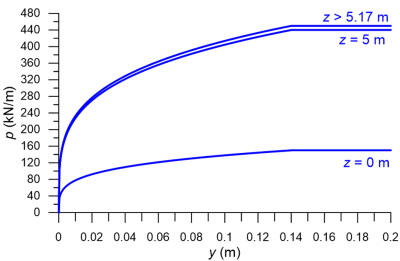
6.27.4 p-y curves for a pile in sand above and below the water table
Step 1:
Determine the friction angle, φ′ of the sand, and its unit weight γ. Consider the submerged unit weight γ′ for sands below the water table (γ′ = γ – γw), and the bulk unit weight γ for sands above the water table.
Step 2:
Compute the ultimate soil reaction per unit length of the pile as the minimum of two values:
(6.151) ![Rendered by QuickLaTeX.com {p_f} = \min \left\{ {\begin{array}{*{20}{c}}{\left( {\gamma z} \right)\left[ {\dfrac{{{K_0}z\tan \varphi '\sin \beta }}{{\tan \left( {\beta - \varphi '} \right)\cos \alpha }} + \dfrac{{\tan \beta }}{{\tan \left( {\beta - \varphi '} \right)}}\left( {D + z\tan \beta \tan \alpha } \right) + {K_0}z\tan \beta \left( {\tan \varphi '\sin \beta - \tan \alpha } \right) - {K_a}D} \right]}\\{\left( {D\gamma z} \right)\left[ {{K_a}\left[ {\left( {{{\tan }^8}\beta } \right) - 1} \right] + {K_0}\tan \varphi '{{\tan }^4}\beta } \right]}\end{array}} \right\}](https://oercollective.caul.edu.au/app/uploads/quicklatex/quicklatex.com-1b393db76df997cc9d7a97ce184a257b_l3.png)
Where α = φ′/2; β = 45⁰ + φ′/2; Κ0 is the earth pressure coefficient at-rest recommended to be taken equal to K0 = 0.6 for loose sand and K0 = 0.4 for dense sand; KA = active earth pressure coefficient KA = tan2(45⁰ – φ′/2).
Step 3:
Use Figure 6.119a and the provided formulas to estimate the value of the factor As as function of depth measured from the soil surface z, and subsequently estimate the soil reaction developing when pile deflection reaches y1 = 3D/80 as:
(6.152) ![]()
![Figure (a) on the left presents the variation of the parameter As with dimensionless depth z/D. For z/D < 3.6 As is calculated as As = e^[1.05-0.322(z/D)] and for z/D > 3.6 As is constant As = 0.88. Figure (b) on the left presents the variation of the parameter Bs with dimensionless depth z/D. For z/D < 4.2 Bs is calculated as Bs = e^[0.8-0.357(z/D)] and for z/D > 4.2 Bs is constant Bs = 0.5.](https://oercollective.caul.edu.au/app/uploads/sites/143/2025/03/6.119-hr-e1743555237163.png)
Step 4:
Use Figure 6.119b and the provided formulas to estimate the value of factor Bs as function of depth measured from the soil surface z, and subsequently estimate the soil reaction developing when pile deflection reaches y2 = D/60 as:
(6.153) ![]()
Step 5:
Estimate the slope of the initial linear of the p-y curve, kpy from Table 6.20, depending on the relative density of the sand and groundwater table conditions.
| Sand density | Sand below the water table | Sand above the water table |
|---|---|---|
| kpy (static, kN/m3) | kpy (static, kN/m3) | |
| Loose | 5400 | 6800 |
| Medium | 16300 | 24400 |
| Dense | 34000 | 61000 |
Step 6:
Determine the factors m, n and C as:
(6.154) ![]()
(6.155) ![]()
(6.156) ![]()
Step 7:
The p-y consists of three linear and one parabolic segment (Figure 6.120), described by the expressions listed in Table 6.21.
| Segment (Figure 6.120) | Pile deflection range, y | Lateral resistance, p |
|---|---|---|
| linear (1) | 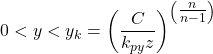 |
|
| parabolic | ||
| linear (2) | ||
| linear (3) |
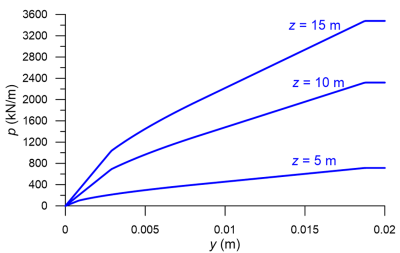
For example, consider a 15-m long pile with diameter D = 0.5 m, driven in medium-dense sand below the water table, with friction angle φ′ = 35º and submerged unit weight γ′ = 9.8 kN/m3. First, the soil resistance is estimated from Eq. 6.151, and accordingly As and Bs are calculated from the expressions provided in Figure 6.119. Assuming kpy = 24000 kN/m3 as an average value from Table 6.19 and K0 = 0.4, we can obtain all the necessary parameters to determine the segments of the p-y curves from Table 6.21, for different elevations z along the pile. Indicatively, for depths z = 5, 10 and 15 m, the parameters of the curves are presented in Table 6.22, and the curves are plotted in Figure 6.121.
| z (m) | pf,1 (kN/m) | pf,2 (kN/m) | As | Bs | p2 (kN/m) | p1 (kN/m) | yk (m) | y2 (m) | y1 (m) |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 811.5 | 1317.9 | 0.88 | 0.50 | 405.7 | 714.1 | 0.000835 | 0.00833 | 0.01875 |
| 10 | 3078.5 | 2635.8 | 0.88 | 0.50 | 1317.9 | 2319.5 | 0.002876 | 0.00833 | 0.01875 |
| 15 | 6801.1 | 3953.8 | 0.88 | 0.50 | 1976.9 | 3479.3 | 0.002876 | 0.00833 | 0.01875 |
A comparison of the indicative p-y curves presented in Figures 6.113, 6.116, 6.118 and 6.121 for clays and sands under variable groundwater table conditions is presented in Figure 6.122, for a typical depth below the ground surface z = 5 m. It is clear that the shape of the curves, and the ultimate reaction developing on the pile, strongly depend on the properties of the surrounding soil, and groundwater table conditions.